Перевернутый маятник - Inverted pendulum

Балансировочная тележка, простая робототехническая система, примерно 1976 г. Тележка содержит сервосистема который контролирует угол наклона стержня и перемещает тележку вперед и назад, чтобы удерживать ее в вертикальном положении.

An перевернутый маятник это маятник это имеет свой центр массы выше его вращаться точка. это неустойчивый и без дополнительной помощи упадет. Его можно стабильно подвешивать в этом перевернутом положении с помощью система контроля следить за углом наклона вехи и перемещать точку поворота по горизонтали назад под центр масс, когда она начинает падать, сохраняя равновесие. Перевернутый маятник - классическая проблема в динамика и теория управления и используется в качестве эталона для тестирования стратегий управления. Это часто реализуется с помощью точки поворота, установленной на тележке, которая может перемещаться горизонтально под управлением электронной сервосистемы, как показано на фотографии; это называется телега и шест аппарат.^[1] Большинство приложений ограничивают маятник до 1 степень свободы прикрепив шест к ось вращения. В то время как нормальный маятник устойчив, когда свешивается вниз, перевернутый маятник нестабилен по своей природе и должен активно балансироваться, чтобы оставаться в вертикальном положении; это можно сделать, применив крутящий момент в точке поворота, перемещая точку поворота по горизонтали как часть Обратная связь система, изменяющая скорость вращения массы, установленной на маятнике на оси, параллельной оси поворота, и, таким образом, создавая чистый крутящий момент на маятнике, или путем колебания точки поворота по вертикали. Простая демонстрация перемещения точки поворота в системе обратной связи достигается балансированием перевернутой метлы на конце пальца.

Второй тип перевернутого маятника - это наклономер для высоких конструкций, который состоит из проволоки, прикрепленной к основанию фундамента и прикрепленной к поплавку в масляной ванне в верхней части конструкции, которая имеет устройства для измерения перемещения нейтрального положения поплавка от его исходного положения .

Обзор

Маятник с карабином, свисающий прямо под опорой вращаться находится в стабильное равновесие точка; на маятник нет крутящего момента, поэтому он останется неподвижным, и при смещении из этого положения будет испытывать восстанавливающий крутящий момент, который возвращает его в положение равновесия. Маятник с опорой в перевернутом положении, опирающийся на жесткий стержень непосредственно над шарниром, на 180 ° от своего устойчивого положения равновесия, находится в неустойчивое равновесие точка. В этот момент на маятник снова нет крутящего момента, но малейшее смещение от этого положения вызовет момент гравитации на маятнике, который разгонит его от равновесия, и он упадет.

Чтобы стабилизировать маятник в этом перевернутом положении, система управления с обратной связью может использоваться, который контролирует угол наклона маятника и перемещает положение точки поворота в сторону, когда маятник начинает падать, чтобы удерживать его в равновесии. Перевернутый маятник - классическая проблема в динамика и теория управления и широко используется как эталон для тестирования алгоритмов управления (ПИД-регуляторы, представление в пространстве состояний, нейронные сети, нечеткое управление, генетические алгоритмы, так далее.). Варианты решения этой проблемы включают несколько звеньев, позволяющих управлять движением тележки при сохранении маятника, а также балансировать систему тележки-маятника на качелях. Перевернутый маятник связан с ракетой или наведением ракеты, где центр тяжести расположен за центром сопротивления, вызывая аэродинамическую нестабильность.^[2] Понимание подобной проблемы может показать простая робототехника в виде балансировочной тележки. Балансировать перевернутую метлу на кончике пальца - это простая демонстрация, и проблема решается путем самобалансировки. личные транспортеры такой как Segway PT, то самобалансирующийся ховерборд и самобалансирующийся одноколесный велосипед.

Другой способ стабилизации перевернутого маятника без какой-либо обратной связи или механизма управления - быстрое колебание оси вращения вверх и вниз. Это называется Маятник капицы. Если колебание является достаточно сильным (с точки зрения его ускорения и амплитуды), то перевернутый маятник может оправиться от возмущений поразительно нелогичным образом. Если точка движения движется внутрь простые гармонические колебания, движение маятника описывается Уравнение Матье.^[3]

Уравнения движения

В уравнения движения Количество перевернутых маятников зависит от того, какие ограничения накладываются на движение маятника. Перевернутые маятники могут быть созданы в различных конфигурациях, что приводит к ряду уравнений движения, описывающих поведение маятника.

Стационарная точка поворота

В конфигурации, где точка поворота маятника зафиксирована в пространстве, уравнение движения аналогично уравнению для необратимый маятник. Уравнение движения ниже предполагает отсутствие трения или любого другого сопротивления движению, жесткий безмассовый стержень и ограничение на 2-мерный движение.

${\displaystyle {\ddot {\theta }}-{g \over \ell }\sin \theta =0}$

Где ${\displaystyle {\ddot {\theta }}}$ это угловое ускорение маятника, ${\displaystyle g}$ это стандартная сила тяжести на поверхности Земли, ${\displaystyle \ell }$ - длина маятника, а ${\displaystyle \theta }$ - угловое смещение, отсчитываемое от положения равновесия.

При добавлении к обеим сторонам он будет иметь тот же знак, что и член углового ускорения:

${\displaystyle {\ddot {\theta }}={g \over \ell }\sin \theta }$

Таким образом, перевернутый маятник будет ускоряться от вертикального неустойчивого равновесия в первоначально смещенном направлении, и ускорение обратно пропорционально длине. Высокие маятники падают медленнее, чем короткие.

Вывод с использованием крутящего момента и момента инерции:

Схематический рисунок перевернутого маятника на тележке. Стержень считается безмассовым. Масса тележки и острие на конце стержня обозначены буквами M и m. Шток имеет длину l.

Предполагается, что маятник состоит из точечной массы массой ${\displaystyle m}$, прикрепленный к концу безмассового жесткого стержня длиной ${\displaystyle \ell }$, прикрепленный к точке поворота в конце, противоположном точечной массе.

Сеть крутящий момент системы должны равняться момент инерции умноженное на угловое ускорение:

${\displaystyle {\boldsymbol {\tau }}_{\mathrm {net} }=I{\ddot {\theta }}}$

Крутящий момент от силы тяжести, обеспечивающий чистый крутящий момент:

${\displaystyle {\boldsymbol {\tau }}_{\mathrm {net} }=mg\ell \sin \theta \,\!}$

Где ${\displaystyle \theta \ }$ - угол, отсчитываемый от перевернутого положения равновесия.

Полученное уравнение:

${\displaystyle I{\ddot {\theta }}=mg\ell \sin \theta \,\!}$

Момент инерции точечной массы:

${\displaystyle I=mR^{2}}$

В случае перевернутого маятника радиус - это длина стержня, ${\displaystyle \ell }$.

Подставляя в ${\displaystyle I=m\ell ^{2}}$

${\displaystyle m\ell ^{2}{\ddot {\theta }}=mg\ell \sin \theta \,\!}$

Масса и ${\displaystyle \ell ^{2}}$ делится с каждой стороны, в результате чего:

${\displaystyle {\ddot {\theta }}={g \over \ell }\sin \theta }$

Перевернутый маятник на тележке

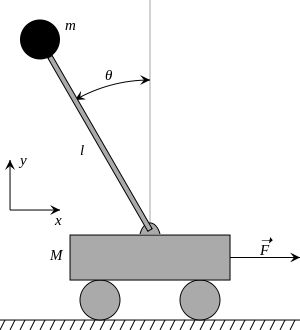
Перевернутый маятник на тележке состоит из массы ${\displaystyle m}$ на вершине шеста длины ${\displaystyle \ell }$ установлен на горизонтально движущемся основании, как показано на соседнем изображении. Корзина ограничена линейное движение и подвержен действию сил, вызывающих или препятствующих движению.

Основы стабилизации

Суть стабилизации перевернутого маятника можно качественно резюмировать в три этапа.

Простая система стабилизации, используемая на тележке с бокалом для вина наверху.

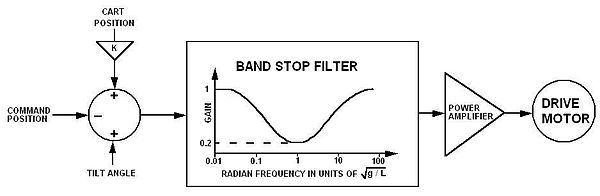
1. Если угол наклона ${\displaystyle \theta }$ находится справа, тележка должна ускоряться вправо и наоборот.

2. Положение тележки ${\displaystyle x}$ относительно центра пути стабилизируется путем небольшой модуляции нулевого угла (угловая ошибка, которую система управления пытается обнулить) положением тележки, то есть нулевым углом ${\displaystyle =\theta +kx}$ куда ${\displaystyle k}$ маленький. Это заставляет веху слегка наклоняться к центру гусеницы и стабилизироваться в центре гусеницы, где угол наклона точно вертикальный. Любое смещение датчика наклона или наклона гусеницы, которое в противном случае могло бы вызвать нестабильность, переводится в стабильное смещение положения. Дополнительное добавленное смещение дает управление положением.

3. Обычный маятник, подверженный движению точки поворота, такой как груз, поднимаемый краном, имеет пиковый отклик на радианной частоте маятника ${\displaystyle \omega _{p}={\sqrt {g/\ell }}}$. Чтобы предотвратить неконтролируемое раскачивание, частотный спектр движения оси должен быть подавлен вблизи ${\displaystyle \omega _{p}}$. Перевернутый маятник требует того же подавляющего фильтра для достижения стабильности.

Обратите внимание, что, как следствие стратегии модуляции нулевого угла, обратная связь по положению является положительной, то есть внезапная команда на движение вправо вызовет начальное движение тележки влево, за которым следует движение вправо, чтобы сбалансировать маятник. Взаимодействие неустойчивости маятника и нестабильности положительной обратной связи по положению для создания устойчивой системы - это особенность, которая делает математический анализ интересной и сложной задачей.

Уравнения Лагранжа

Уравнения движения могут быть получены с использованием Уравнения Лагранжа. Обратимся к рисунку справа, где ${\displaystyle \theta (t)}$ угол маятника длины ${\displaystyle l}$ относительно вертикального направления и действующими силами являются сила тяжести и внешняя сила F в x-направлении. Определять ${\displaystyle x(t)}$ быть позицией тележки.

Кинетический ${\displaystyle T}$ системы:

${\displaystyle T={\frac {1}{2}}Mv_{1}^{2}+{\frac {1}{2}}mv_{2}^{2},}$

куда ${\displaystyle v_{1}}$ - скорость тележки и ${\displaystyle v_{2}}$ - скорость точечной массы ${\displaystyle m}$.${\displaystyle v_{1}}$ и ${\displaystyle v_{2}}$ можно выразить через x и ${\displaystyle \theta }$ записав скорость как первую производную от положения;

${\displaystyle v_{1}^{2}={\dot {x}}^{2},}$

${\displaystyle v_{2}^{2}=\left({\frac {\rm {d}}{{\rm {d}}t}}{\left(x-\ell \sin \theta \right)}\right)^{2}+\left({\frac {\rm {d}}{{\rm {d}}t}}{\left(\ell \cos \theta \right)}\right)^{2}.}$

Упрощая выражение для ${\displaystyle v_{2}}$ приводит к:

${\displaystyle v_{2}^{2}={\dot {x}}^{2}-2\ell {\dot {x}}{\dot {\theta }}\cos \theta +\ell ^{2}{\dot {\theta }}^{2}.}$

Кинетическая энергия теперь определяется как:

${\displaystyle T={\frac {1}{2}}\left(M+m\right){\dot {x}}^{2}-m\ell {\dot {x}}{\dot {\theta }}\cos \theta +{\frac {1}{2}}m\ell ^{2}{\dot {\theta }}^{2}.}$

Обобщенные координаты системы: ${\displaystyle \theta }$ и ${\displaystyle x}$, у каждого есть обобщенная сила. ${\displaystyle x}$ ось, обобщенная сила ${\displaystyle Q_{x}}$ можно рассчитать через его виртуальную работу

${\displaystyle Q_{x}\delta x=F\delta x,\quad Q_{x}=F,}$

на ${\displaystyle \theta }$ ось, обобщенная сила ${\displaystyle Q_{\theta }}$ можно также рассчитать через его виртуальную работу

${\displaystyle Q_{\theta }\delta \theta =mgl\sin \theta \delta \theta ,\quad Q_{\theta }=mgl\sin \theta .}$

Согласно Уравнения Лагранжа, уравнения движения:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}{\partial {T} \over \partial {\dot {x}}}-{\partial {T} \over \partial x}=F,}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}{\partial {T} \over \partial {\dot {\theta }}}-{\partial {T} \over \partial \theta }=mgl\sin \theta ,}$

замена ${\displaystyle T}$ в этих уравнениях и упрощение приводит к уравнениям, которые описывают движение перевернутого маятника:

${\displaystyle \left(M+m\right){\ddot {x}}-m\ell {\ddot {\theta }}\cos \theta +m\ell {\dot {\theta }}^{2}\sin \theta =F,}$

${\displaystyle \ell {\ddot {\theta }}-g\sin \theta ={\ddot {x}}\cos \theta .}$

Эти уравнения нелинейны, но, поскольку цель системы управления - удерживать маятник в вертикальном положении, уравнения можно линеаризовать вокруг ${\displaystyle \theta \approx 0}$.

Уравнение Эйлера-Лагранжа

Обобщенные силы можно записать как потенциальную энергию ${\displaystyle V_{x}}$ и ${\displaystyle V_{\theta }}$,

Обобщенные силы	Потенциальная энергия
${\displaystyle Q_{x}=F}$	${\displaystyle V_{x}=\int _{t_{0}}^{t}F{\dot {x}}\ {\rm {d}}t}$
${\displaystyle Q_{\theta }=mgl\sin \theta }$	${\displaystyle V_{\theta }=mgl\cos \theta }$

Согласно Принцип Даламбера, обобщенные силы и потенциальная энергия связаны:

${\displaystyle Q_{j}={\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial V}{\partial {\dot {q}}_{j}}}-{\frac {\partial V}{\partial q_{j}}}\,,}$

Однако при определенных обстоятельствах потенциальная энергия недоступна, доступны только обобщенные силы.

После получения Лагранжиан ${\displaystyle {\mathcal {L}}=T-V}$, мы также можем использовать Уравнение Эйлера – Лагранжа. решить для уравнений движения:

${\displaystyle {\frac {\partial {\mathcal {L}}}{\partial x}}-{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial {\mathcal {L}}}{\partial {\dot {x}}}}\right)=0}$,

${\displaystyle {\frac {\partial {\mathcal {L}}}{\partial \theta }}-{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial {\mathcal {L}}}{\partial {\dot {\theta }}}}\right)=0}$.

Единственная разница в том, следует ли включать обобщенные силы в потенциальную энергию ${\displaystyle V_{j}}$ или напишите их явно как ${\displaystyle Q_{j}}$ с правой стороны, все они приводят к одним и тем же уравнениям в финале.

Второй закон Ньютона

Часто полезно использовать Второй закон Ньютона вместо Уравнения Лагранжа потому что уравнения Ньютона определяют силы реакции на стыке маятника и тележки. Эти уравнения приводят к двум уравнениям для каждого тела; один в направлении x, а другой - в направлении y. Уравнения движения тележки показаны ниже, где LHS - это сумма сил, действующих на тело, а RHS - ускорение.

${\displaystyle F-R_{x}=M{\ddot {x}}}$

${\displaystyle F_{N}-R_{y}-Mg=0}$

В приведенных выше уравнениях ${\displaystyle R_{x}}$ и ${\displaystyle R_{y}}$ - силы реакции в суставе. ${\displaystyle F_{N}}$ нормальная сила, приложенная к тележке. Это второе уравнение зависит только от вертикальной силы реакции, поэтому уравнение можно использовать для определения нормальной силы. Первое уравнение можно использовать для определения силы горизонтальной реакции. Чтобы завершить уравнения движения, необходимо вычислить ускорение точечной массы, прикрепленной к маятнику. Положение точечной массы может быть задано в инерциальных координатах как

${\displaystyle {\vec {r}}_{P}=(x-\ell \sin \theta ){\hat {x}}_{I}+\ell \cos \theta {\hat {y}}_{I}}$

Взяв две производные, получаем вектор ускорения в инерциальной системе отсчета.

${\displaystyle {\vec {a}}_{P/I}=({\ddot {x}}+\ell {\dot {\theta }}^{2}\sin \theta -\ell {\ddot {\theta }}\cos \theta ){\hat {x}}_{I}+(-\ell {\dot {\theta }}^{2}\cos \theta -\ell {\ddot {\theta }}\sin \theta ){\hat {y}}_{I}}$

Затем, используя второй закон Ньютона, можно записать два уравнения в направлении x и y. Обратите внимание, что силы реакции положительны при приложении к маятнику и отрицательны при приложении к тележке. Это связано с третьим законом Ньютона.

${\displaystyle R_{x}=m({\ddot {x}}+\ell {\dot {\theta }}^{2}\sin \theta -\ell {\ddot {\theta }}\cos \theta )}$

${\displaystyle R_{y}-mg=m(-\ell {\dot {\theta }}^{2}\cos \theta -\ell {\ddot {\theta }}\sin \theta )}$

Первое уравнение позволяет еще одним способом вычислить горизонтальную силу реакции в случае, если приложенная сила ${\displaystyle F}$ не известно. Второе уравнение можно использовать для определения силы вертикальной реакции. Первое уравнение движения получается заменой ${\displaystyle F-R_{x}=M{\ddot {x}}}$ в ${\displaystyle R_{x}=m({\ddot {x}}+\ell {\dot {\theta }}^{2}\sin \theta -\ell {\ddot {\theta }}\cos \theta )}$ что дает

${\displaystyle \left(M+m\right){\ddot {x}}-m\ell {\ddot {\theta }}\cos \theta +m\ell {\dot {\theta }}^{2}\sin \theta =F}$

При осмотре это уравнение идентично результату метода Лагранжа. Чтобы получить второе уравнение, уравнение движения маятника должно быть обозначено единичным вектором, который всегда проходит перпендикулярно маятнику и обычно обозначается как координата x рамы тела. В инерциальных координатах этот вектор может быть записан с помощью простого двумерного преобразования координат

${\displaystyle {\hat {x}}_{B}=\cos \theta {\hat {x}}_{I}+\sin \theta {\hat {y}}_{I}}$

Уравнение движения маятника, записанное в векторной форме, имеет вид ${\displaystyle \sum {\vec {F}}=m{\vec {a}}_{P/I}}$. Точки ${\displaystyle {\hat {x}}_{B}}$ с обеих сторон дает следующее на левой стороне (обратите внимание, что транспонирование аналогично скалярному произведению)

${\displaystyle ({\hat {x}}_{B})^{T}\sum {\vec {F}}=({\hat {x}}_{B})^{T}(R_{x}{\hat {x}}_{I}+R_{y}{\hat {y}}_{I}-mg{\hat {y}}_{I})=({\hat {x}}_{B})^{T}(R_{p}{\hat {y}}_{B}-mg{\hat {y}}_{I})=-mg\sin \theta }$

В приведенном выше уравнении используется соотношение между компонентами сил реакции корпуса и инерционными компонентами сил реакции. Предположение о том, что стержень, соединяющий точечную массу с тележкой, не имеет массы, означает, что этот стержень не может передавать нагрузку перпендикулярно стержню. Таким образом, компоненты сил реакции инерциальной системы отсчета можно записать просто как ${\displaystyle R_{p}{\hat {y}}_{B}}$ Это означает, что стержень может передавать нагрузки только вдоль оси самого стержня. Это приводит к другому уравнению, которое можно использовать для определения натяжения самого стержня.

${\displaystyle R_{p}={\sqrt {R_{x}^{2}+R_{y}^{2}}}}$

Правая часть уравнения вычисляется аналогично путем расстановки точек ${\displaystyle {\hat {x}}_{B}}$ с ускорением маятника. Результат (после некоторого упрощения) показан ниже.

${\displaystyle m({\hat {x}}_{B})^{T}({\vec {a}}_{P/I})=m({\ddot {x}}\cos \theta -\ell {\ddot {\theta }})}$

Объединение LHS с RHS и деление на m дает

${\displaystyle \ell {\ddot {\theta }}-g\sin \theta ={\ddot {x}}\cos \theta }$

что опять же идентично результату метода Лагранжа. Преимущество использования метода Ньютона заключается в том, что проявляются все силы реакции, гарантирующие, что ничто не будет повреждено.

Чертеж, показывающий, как может быть построен маятник Капицы: двигатель вращает кривошип с высокой скоростью, кривошипно вибрирует рычаг вверх и вниз, к которому маятник прикреплен с помощью оси.

Маятник капицы

Основная статья: Маятник капицы

Перевернутый маятник, в котором стержень быстро колеблется вверх и вниз, может быть устойчивым в перевернутом положении. Это называется Маятник капицы, в честь русского физика Петр Капица кто первым проанализировал это. Уравнение движения маятника, соединенного с безмассовым колеблющимся основанием, выводится так же, как и для маятника на тележке. Положение точечной массы теперь определяется следующим образом:

${\displaystyle \left(-\ell \sin \theta ,y+\ell \cos \theta \right)}$

а скорость находится путем взятия первой производной от положения:

${\displaystyle v^{2}={\dot {y}}^{2}-2\ell {\dot {y}}{\dot {\theta }}\sin \theta +\ell ^{2}{\dot {\theta }}^{2}.}$

Графики перевернутого маятника на колебательной основе. Первый график показывает реакцию маятника на медленное колебание, второй - реакцию на быстрое колебание.

В Лагранжиан для этой системы можно записать как:

${\displaystyle L={\frac {1}{2}}m\left({\dot {y}}^{2}-2\ell {\dot {y}}{\dot {\theta }}\sin \theta +\ell ^{2}{\dot {\theta }}^{2}\right)-mg\left(y+\ell \cos \theta \right)}$

а уравнение движения следует из:

${\displaystyle {\mathrm {d} \over \mathrm {d} t}{\partial {L} \over \partial {\dot {\theta }}}-{\partial {L} \over \partial \theta }=0}$

в результате чего:

${\displaystyle \ell {\ddot {\theta }}-{\ddot {y}}\sin \theta =g\sin \theta .}$

Если у представляет простые гармонические колебания, ${\displaystyle y=A\sin \omega t}$, следующее дифференциальное уравнение является:

${\displaystyle {\ddot {\theta }}-{g \over \ell }\sin \theta =-{A \over \ell }\omega ^{2}\sin \omega t\sin \theta .}$

Это уравнение не имеет элементарных решений в замкнутой форме, но его можно исследовать различными способами. Это близко приближается к Уравнение Матье, например, при малой амплитуде колебаний. Анализ показывает, что маятник остается в вертикальном положении при быстрых колебаниях. Первый график показывает, что когда ${\displaystyle y}$ представляет собой медленное колебание, маятник быстро падает при отклонении от вертикального положения. Угол ${\displaystyle \theta }$ через короткое время превышает 90 °, что означает, что маятник упал на землю. Если ${\displaystyle y}$ это быстрое колебание, маятник может оставаться стабильным в вертикальном положении. Второй график показывает, что при отклонении от вертикального положения маятник начинает колебаться вокруг вертикального положения (${\displaystyle \theta =0}$). Отклонение от вертикального положения остается небольшим, и маятник не опрокидывается.

Виды перевернутых маятников

Достижение устойчивости перевернутого маятника стало общей инженерной задачей для исследователей.^[4] Существуют различные вариации перевернутого маятника на тележке, от стержня на тележке до многосегментного перевернутого маятника на тележке. В другом варианте стержень перевернутого маятника или сегментированный стержень помещается на конец вращающегося узла. В обоих случаях (тележка и вращающаяся система) перевернутый маятник может падать только в плоскости. Перевернутые маятники в этих проектах могут потребоваться либо для поддержания баланса только после того, как равновесное положение достигнуто, либо для достижения равновесия самостоятельно. Еще одна площадка - двухколесный балансировочный перевернутый маятник. Двухколесная платформа способна вращаться на месте, обеспечивая большую маневренность.^[5] Еще один вариант основан на одном моменте. А волчок, а одноколесный велосипед, или перевернутый маятник на сферическом шаре, балансирующий в одной точке. Как показано выше, перевернутый маятник может быть также получен с помощью вертикально колеблющегося основания.

Примеры перевернутых маятников

Пожалуй, наиболее распространенным примером стабилизированного перевернутого маятника является человек. Человек, стоящий в вертикальном положении, действует как перевернутый маятник, опираясь на ноги, и без постоянных небольших мышечных изменений он упадет. Нервная система человека содержит бессознательное Обратная связь система контроля, то Чувство равновесия или же восстанавливающий рефлекс, который использует проприоцептивный ввод от глаз, мышц и суставов, а также ввод ориентации от вестибулярный аппарат состоящий из трех полукружные каналы в внутреннее ухо, и два отолит органы, чтобы постоянно вносить небольшие изменения в скелетные мышцы, чтобы удерживать нас в вертикальном положении. Ходьба, бег или балансирование на одной ноге предъявляют дополнительные требования к этой системе. Некоторые заболевания, а также алкогольное или наркотическое опьянение могут мешать этому рефлексу, вызывая головокружение и нарушение равновесия, неспособность стоять прямо. А полевой тест на трезвость используется полицией для проверки водителей на алкоголь или наркотики, проверяет этот рефлекс на предмет нарушения.

Вот несколько простых примеров: балансировка метел или счетчиков вручную.

Перевернутый маятник использовался в различных устройствах, и попытка сбалансировать перевернутый маятник представляет собой уникальную инженерную проблему для исследователей.^[6] Перевернутый маятник был центральным компонентом в конструкции нескольких ранних сейсмометры из-за присущей ей нестабильности, приводящей к измеримой реакции на любые помехи.^[7]

Модель перевернутого маятника использовалась в некоторых недавних личные транспортеры, например, двухколесный самобалансирующиеся самокаты и одноколесные электрические моноциклы. Эти устройства кинематически нестабильны и используют электронную обратную связь. сервосистема держать их в вертикальном положении.

Приведение маятника на тележке в состояние перевернутого маятника считается традиционной игрушечной задачей / эталоном оптимального управления.^[8][9]

Траектория вертикального поворота каретки с фиксированным временем, сводящая к минимуму квадрат силы

Смотрите также

• Двойной перевернутый маятник
• Маятник инерционного колеса
• Маятник Furuta
• iBOT
• Гуманоидный робот
• Ballbot

Рекомендации

1. C.A. Проект старшего колледжа Гамильтона Юнион 1966
2. https://www.grc.nasa.gov/WWW/k-12/VirtualAero/BottleRocket/airplane/rktstab.html
3. http://www2.math.ou.edu/~npetrov/joe-report.pdf
4. http://robotics.ee.uwa.edu.au/theses/2003-Balance-Ooi.pdf
5. «Архивная копия» (PDF). Архивировано из оригинал (PDF) на 2016-03-04. Получено 2012-05-01.
6. «Архивная копия» (PDF). Архивировано из оригинал (PDF) на 2016-03-04. Получено 2012-05-01.
7. https://earthquake.usgs.gov/learn/topics/seismology/history/part12.php
8. "Акробот и тележка-шест" (PDF).
9. "Тележка-качалка". www.cs.huji.ac.il. Получено 2019-08-19.

• Д. Либерзон Коммутация в системах и управлении (2003 Springer) стр. 89 и далее

дальнейшее чтение

• Франклин; и другие. (2005). Управление с обратной связью динамических систем, 5, Прентис Холл. ISBN  0-13-149930-0

внешняя ссылка

• YouTube - Перевернутый маятник - Демо № 3
• YouTube - перевернутый маятник
• YouTube - Двойной маятник на тележке
• YouTube - Тройной маятник на тележке
• Динамическое моделирование перевернутого маятника на колебательном основании.
• Перевернутый маятник: анализ, проектирование и реализация
• Нелинейное качание и стабилизирующее управление перевернутой маятниковой системой
• Нечеткое стабилизационное управление системами перевернутого маятника^{[постоянная мертвая ссылка ]}
• Сообщение в блоге о перевернутом маятнике с кодом Python
• Уравнения движения для задачи управления тележкой и мачтой.