Приближение пустой решетки - Empty lattice approximation
В приближение пустой решетки теоретический электронная зонная структура модель, в которой потенциал периодический и слабый (близка к постоянной). Можно также считать пустой[требуется разъяснение ] нерегулярная решетка, в которой потенциал даже не периодичен.[1] Приближение пустой решетки описывает ряд свойств энергодисперсионных соотношений невзаимодействующих свободные электроны которые проходят через кристаллическая решетка. Энергия электронов в «пустой решетке» такая же, как энергия свободных электронов. Модель полезна, поскольку она ясно иллюстрирует ряд иногда очень сложных особенностей соотношений дисперсии энергии в твердых телах, которые являются фундаментальными для всех электронных зонных структур.
Рассеяние и периодичность

Периодический потенциал решетки в этой модели свободных электронов должен быть слабым, потому что в противном случае электроны не были бы свободными. Сила рассеяния в основном зависит от геометрии и топологии системы. Топологически определенные параметры, например рассеяние поперечные сечения, зависят от величины потенциала и размера потенциальная яма. Для 1-, 2- и 3-мерных пространств потенциальные ямы всегда рассеивают волны, независимо от того, насколько малы их потенциалы, каковы их знаки или насколько ограничены их размеры. Для частицы в одномерной решетке, такой как Модель Кронига – Пенни, можно рассчитать зонную структуру аналитически, подставив значения для потенциала, шага решетки и размера потенциальной ямы.[2] Для двумерных и трехмерных задач сложнее точно рассчитать ленточную структуру на основе аналогичной модели с несколькими параметрами. Тем не менее свойства зонной структуры в большинстве областей легко аппроксимировать формулой методы возмущения.
Теоретически решетка бесконечно велика, поэтому слабый периодический потенциал рассеяния в конечном итоге будет достаточно сильным, чтобы отразить волну. Процесс рассеяния приводит к хорошо известному Размышления Брэгга электронов периодическим потенциалом Кристальная структура. Отсюда периодичность дисперсионного соотношения и деление k-пространство в зонах Бриллюэна. Соотношение периодической дисперсии энергии выражается как:
В являются обратная решетка векторы, к которым полосы[требуется разъяснение ] принадлежать.
На рисунке справа показано дисперсионное соотношение для трех периодов в обратном пространстве одномерной решетки с ячейками длины а.
Энергетические зоны и плотность состояний
В одномерной решетке число векторов обратной решетки которые определяют полосы в интервале энергий, ограничивается двумя, когда энергия возрастает. В двумерных и трехмерных решетках количество векторов обратной решетки, определяющих зоны свободных электронов увеличивается быстрее, когда увеличивается длина волнового вектора и растет энергия. Это связано с тем, что количество векторов обратной решетки которые лежат в интервале увеличивается. В плотность состояний в энергетическом интервале зависит от количества состояний в интервале в обратном пространстве и наклон дисперсионного соотношения .

Хотя ячейки решетки не являются сферически симметричными, дисперсионное соотношение по-прежнему имеет сферическую симметрию с точки зрения фиксированной центральной точки в ячейке обратной решетки, если дисперсионное соотношение распространяется за пределы центральной зоны Бриллюэна. В плотность состояний в трехмерной решетке будет такой же, как и в случае отсутствия решетки. Для трехмерного случая плотность состояний является;
В трехмерном пространстве границы зоны Бриллюэна - плоскости. Дисперсионные соотношения показывают коники парабол энергетической дисперсии свободных электронов для всех возможных векторов обратной решетки. Это приводит к очень сложному набору пересечений кривых при вычислении дисперсионных соотношений, поскольку существует большое количество возможных углов между оценочными траекториями, границами зоны Бриллюэна первого и более высокого порядка и конусами пересечения дисперсионных парабол.
Вторая, третья и высшие зоны Бриллюэна
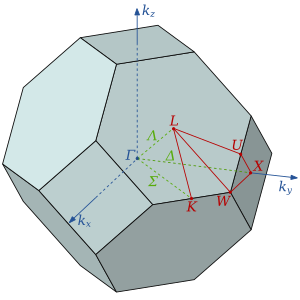
«Свободные электроны», движущиеся по решетке твердого тела с волновыми векторами. далеко за пределами первой зоны Бриллюэна все еще отражаются обратно в первую зону Бриллюэна. Увидеть внешняя ссылка раздел для сайтов с примерами и рисунками.
Модель почти свободных электронов
В большинстве простые металлы, подобно алюминий, то экранирующий эффект сильно уменьшает электрическое поле ионов в твердом теле. Электростатический потенциал выражается как
куда Z это атомный номер, е - элементарный заряд единицы, р - расстояние до ядра внедренного иона и q - параметр экранирования, определяющий диапазон потенциала. В преобразование Фурье, , потенциала решетки, , выражается как
Когда значения недиагональных элементов между векторами обратной решетки в гамильтониане почти равны нулю. В результате величина запрещенной зоны коллапсирует, и получается приближение пустой решетки.
Электронные зоны обычных металлических кристаллов
За исключением нескольких экзотических исключений, металлы кристаллизоваться в трех видах кристаллических структур: BCC и FCC кубические кристаллические структуры и шестиугольник плотно упакованный HCP Кристальная структура.

Телоцентрированный кубический (I)

Гранецентрированный кубический (F)
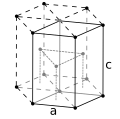
Гексагональный плотно упакованный


Рекомендации
- ^ Конспект лекций по физике. П. Дирак, Фейнман Р., 1968. Интернет, Amazon, 25.03.2014.
- ^ К. Киттель (1953–1976). Введение в физику твердого тела. Wiley & Sons. ISBN 978-0-471-49024-1.




![{ displaystyle [ mathbf {k}, mathbf {k} + d mathbf {k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d7ef6c35b7860d5b4499452122c656105049a98)
![[E, E + dE]](https://wikimedia.org/api/rest_v1/media/math/render/svg/07f5628553913c540c6c4dcadfb657de061b5913)










