Начертательная геометрия - Descriptive geometry
Эта статья поднимает множество проблем. Пожалуйста помоги Улучши это или обсудите эти вопросы на страница обсуждения. (Узнайте, как и когда удалить эти сообщения-шаблоны) (Узнайте, как и когда удалить этот шаблон сообщения)
|
Начертательная геометрия это филиал геометрия который позволяет представлять трехмерные объекты в двух измерениях с помощью определенного набора процедур. Полученные приёмы важны для инженерное дело, архитектура, дизайн И в Изобразительное искусство.[1] Теоретическая основа начертательной геометрии обеспечивается плоские геометрические проекции. Самой ранней известной публикацией по этой технике была «Underweysung der Messung mit dem Zirckel und Richtscheyt», опубликованная в Linien, Нюрнберг: 1525 г. Альбрехт Дюрер. Итальянский архитектор Гуарино Гуарини был также пионером проективной и начертательной геометрии, как видно из егоPlacita Philosophica (1665), Евклид Адауктус (1671) и Architettura Civile (1686 - не опубликовано до 1737), предвосхищая работу Гаспара Монжа (1746–1818), которому обычно приписывают изобретение начертательной геометрии.[2][3] Гаспар Монж обычно считается «отцом начертательной геометрии» из-за его достижений в решении геометрических задач. Его первые открытия были сделаны в 1765 году, когда он работал чертежником военных укреплений, хотя его результаты были опубликованы позже.[4]
Протоколы Монжа позволяют рисовать воображаемый объект таким образом, чтобы его можно было смоделировать в трех измерениях. Все геометрические аспекты воображаемого объекта учитываются в истинном размере / масштабе и форме, и их можно отобразить так, как это видно из любой точки пространства. Все изображения представлены на двухмерной поверхности.
Начертательная геометрия использует технику создания изображений, когда воображаемые параллельные проекторы исходят из воображаемого объекта и пересекают воображаемую плоскость проекции под прямым углом. Суммарные точки пересечений создают желаемое изображение.
Протоколы
- Спроецируйте два изображения объекта во взаимно перпендикулярные произвольные направления. Каждый вид изображения вмещает три измерения пространства, два измерения отображаются в виде полноразмерных взаимно перпендикулярных осей и одно в виде невидимой (точечной) оси, уходящей в пространство изображения (глубина). Каждое из двух соседних изображений представляет собой полноразмерный вид одного из трех измерений пространства.
- Любое из этих изображений может служить отправной точкой для третьего проецируемого вида. Третий вид может начинать четвертую проекцию, причем до бесконечности. Каждая из этих последовательных проекций представляет собой окольный поворот на 90 ° в пространстве, чтобы рассмотреть объект с другого направления.
- Каждая новая проекция использует размер в полном масштабе, который отображается как размер точки на предыдущем виде. Чтобы получить полноразмерный вид этого измерения и разместить его в новом виде, необходимо игнорировать предыдущий вид и перейти ко второму предыдущему виду, где это измерение отображается в полном масштабе.
- Каждый новый вид может быть создан путем проецирования в любое из бесконечного числа направлений, перпендикулярных предыдущему направлению проецирования. (Представьте себе множество направлений спиц колеса телеги, каждое из которых перпендикулярно направлению оси.) Результатом является обход объекта с поворотом на 90 ° и наблюдение объекта с каждого шага. Каждое новое представление добавляется как дополнительное представление к орфографическая проекция макет дисплея и появляется в «разворачивании модели стеклянной коробки».
Помимо ортогонального, шести стандартных основных видов (спереди; справа; слева; сверху; снизу; сзади), описательная геометрия стремится дать четыре основных вида решения: истинная длина линии (т. е. в полный размер, без ракурса), точечный вид (вид с торца) линии, истинная форма плоскости (т. е. полный размер в масштабе или без ракурса) и вид плоскости с краю (т. е. вид на самолет с линией визирования, перпендикулярной линии визирования, связанной с линией визирования, для получения истинной формы плоскости). Они часто служат для определения направления проекции для последующего просмотра. Благодаря процессу обходного шага на 90 °, проецирование в любом направлении с точки зрения линии дает ее истинная длина Посмотреть; проецирование в направлении, параллельном виду линии истинной длины, дает его вид точки, проецирование вида точки любой линии на плоскости дает вид края плоскости; проецирование в направлении, перпендикулярном краю плоскости, даст вид истинной формы (в масштабе). Эти различные представления могут быть использованы для решения инженерных проблем, связанных с принципами твердотельной геометрии.
Эвристика
Изучение начертательной геометрии имеет эвристическую ценность. Он развивает способности к визуализации и пространственному анализу, а также интуитивную способность распознавать направление взгляда для наилучшего представления геометрической задачи для решения. Типичные примеры:
Лучшее направление для просмотра
- Два косые линии (трубы, возможно) в общих положениях, чтобы определить расположение их кратчайшего соединителя (общий перпендикуляр)
- Две наклонные линии (трубы) в общих положениях, так что их самый короткий соединитель виден в полном масштабе
- Две наклонные линии в общих положениях, такие как самый короткий соединитель, параллельный заданной плоскости, видны в полном масштабе (например, для определения положения и размера самого короткого соединителя на постоянном расстоянии от излучающей поверхности)
- Плоская поверхность, на которой просверленное перпендикулярное отверстие видно в полном масштабе, как если бы вы смотрели через отверстие (скажем, для проверки зазоров с другими просверленными отверстиями)
- Плоскость, равноудаленная от двух наклонных линий в общих положениях (скажем, для подтверждения безопасного радиационного расстояния?)
- Кратчайшее расстояние от точки до плоскости (скажем, чтобы найти наиболее экономичное положение для крепления)
- Линия пересечения двух поверхностей, включая криволинейные поверхности (скажем, для наиболее экономичного определения размеров секций?)
- Истинный размер угла между двумя плоскостями
Стандарт для представления видов компьютерного моделирования, аналогичных ортогональным последовательным проекциям, еще не принят. Один из кандидатов в таковые представлен на иллюстрациях ниже. Изображения на иллюстрациях созданы с использованием трехмерной инженерной компьютерной графики.
Трехмерное компьютерное моделирование создает виртуальное пространство «за трубкой», так сказать, и может производить любой вид модели с любого направления в этом виртуальном пространстве. Это делает это без необходимости в смежных орфографических представлениях и, следовательно, может показаться, что обходной пошаговый протокол описательной геометрии устарел. Однако, поскольку начертательная геометрия - это наука о законном или допустимом отображении трех или более Пространство измерения на плоской плоскости является незаменимым исследованием для расширения возможностей компьютерного моделирования.
Примеры
Нахождение кратчайшего соединителя между двумя заданными перекосами PR и SU

Учитывая координаты X, Y и Z точек P, R, S и U, проекции 1 и 2 отображаются в масштабе в плоскостях X-Y и X-Z соответственно.
Чтобы получить истинное изображение (длина в проекции равна длине в трехмерном пространстве) одной из линий: SU в этом примере проекция 3 нарисована с линией петли H2,3 параллельно S2U2. Чтобы получить вид SU с торца, на проекции 4 проведена линия петли H3,4 перпендикулярно S3U3. Перпендикулярное расстояние d дает кратчайшее расстояние между PR и SU.
Чтобы получить точки Q и T на этих линиях, дающие это кратчайшее расстояние, проекция 5 строится с линией петли H.4,5 параллельно P4р4, делая как P5р5 и S5U5 истинные виды (истинным видом считается любая проекция вида с торца). Проецируя пересечение этих прямых, Q5 и т5 назад к проекции 1 (пурпурные линии и метки) позволяет считывать их координаты по осям X, Y и Z.
Общие решения
Общие решения - это класс решений в начертательной геометрии, который содержит все возможные решения проблемы. Общее решение представлено одним трехмерным объектом, обычно конусом, направления элементов которого являются желаемым направлением обзора (проекцией) для любого из бесконечного числа видов решения.
Например: чтобы найти общее решение, при котором появляются две косые линии разной длины в общих положениях (скажем, ракеты в полете?):
- Равной длины
- Равной длины и параллельности
- Равной длины и перпендикулярно (например, для идеального прицеливания хотя бы одного)
- Равно длинам указанного соотношения
- другие.
В примерах общее решение для каждого желаемого характеристического решения представляет собой конус, каждый элемент которого дает одно из бесконечного числа представлений решения. Когда две или более характеристики, скажем, перечисленные выше, желательны (и для которых существует решение), проецирование в направлении любого из двух элементов пересечения (один элемент, если конусы касаются) между двумя конусами дает желаемое вид решения. Если конусы не пересекаются, решения не существует. Приведенные ниже примеры аннотированы, чтобы показать наглядные геометрические принципы, используемые в решениях. TL = истинная длина; EV = вид с края.
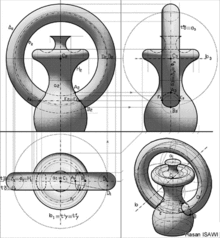
Рис. 1-3 ниже демонстрируют (1) начертательную геометрию, общие решения и (2) одновременно потенциальный стандарт для представления таких решений в ортогональных, многовидовых форматах макета.
В потенциальном стандарте используются два смежных стандартных ортогональных вида (здесь спереди и сверху) со стандартной «линией сгиба» между ними. Поскольку в стандартных двухэтапных последовательностях, чтобы получить представление решения (можно сразу перейти к представлению решения), нет необходимости `` обходить '' объект на 90 °, этот более короткий протокол учитывается для в макете. Если одноэтапный протокол заменяет двухэтапный протокол, используются линии «двойного сворачивания». Другими словами, когда кто-то пересекает двойные линии, он совершает не обходной поворот на 90 °, а неортонаправленный поворот непосредственно к виду решения. Поскольку большинство пакетов инженерной компьютерной графики автоматически генерирует шесть основных видов модели стеклянного ящика, а также изометрический вид, эти виды иногда добавляются из эвристического любопытства.

Рисунок 1: Начертательная геометрия - наклонные линии кажутся перпендикулярными

Рисунок 2: Начертательная геометрия - наклонные линии кажутся равной длины
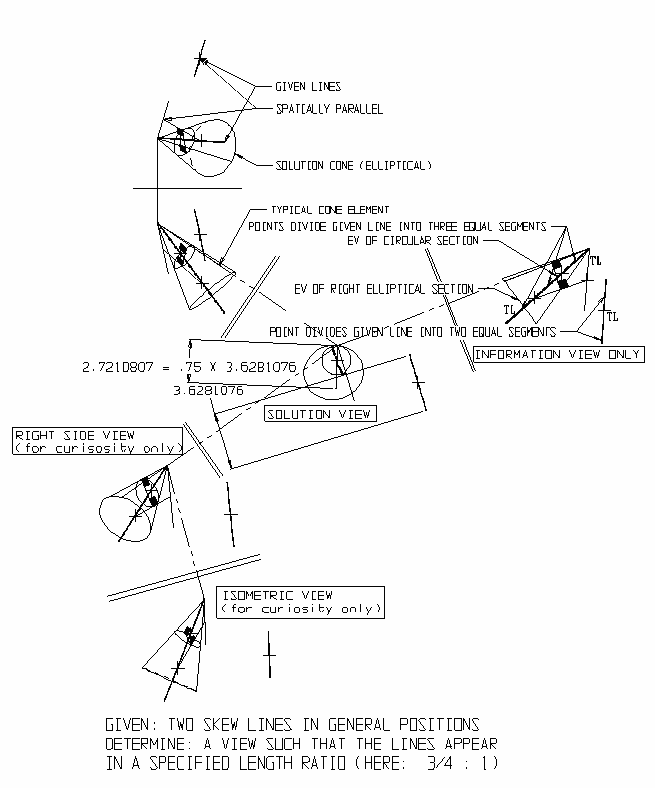
Рисунок 3: Начертательная геометрия - наклонные линии появляются с заданным соотношением длины
Смотрите также
Рекомендации
- ^ Иосиф Малькевич (апрель 2003 г.), «Математика и искусство», Архив столбца функций, Американское математическое общество
- ^ Джеймс Стивенс Кёрл, изд. (2015). «Гуарини, Гуарино». Словарь архитектуры. Oxford University Press. п. 337. ISBN 9780198606789.
- ^ Бьянкини, Карло (2012). "Роль стереотомии в космических исследованиях Гуарино Гуарини". Гайки и болты истории строительства. 1: 257–263. ISBN 978-2-7084-0929-3.
- ^ Ингрид Карлбом, Джозеф Пасиорек (декабрь 1978 г.), «Плоские геометрические проекции и трансформации просмотра», Опросы ACM Computing, 10 (4): 465–502, CiteSeerX 10.1.1.532.4774, Дои:10.1145/356744.356750, S2CID 708008


