Круг замешательства - Circle of confusion

По близкой теме микроскопии см. Функция распределения точки.

Диаграмма, показывающая круги нерезкости для точечного источника, расположенного слишком близко, в фокусе и слишком далеко

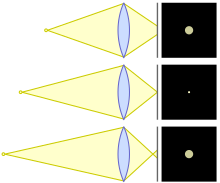
В оптика, а круг замешательства оптическое пятно, образованное конусом света лучи из линза не приходит к идеалу фокус при визуализации точечный источник. Он также известен как диск замешательства, круг нечеткости, размытие круга, или пятно размытия.

В фотографии кружок неразберихи (CoC) используется для определения глубина резкости, часть изображения с приемлемой резкостью. Стандартное значение CoC часто связано с каждым формат изображения, но наиболее подходящее значение зависит от Острота зрения, условия просмотра и степень увеличения. Использование в контексте включает максимально допустимый круг нечеткости, предел диаметра круга нерезкости, а критерий круга нечеткости.

Настоящие линзы не сосредотачивайся все лучи идеально подходят, так что даже при наилучшей фокусировке точка отображается как пятно, а не как точка. Наименьшее такое пятно, которое может создать линза, часто называют круг наименьшего замешательства.

Два использования

Следует различать два важных использования этого термина и концепции:

В идеальном объективе L, все лучи проходят через точку фокусировки F. Однако на других расстояниях от линзы лучи образуют круг.

1. Для описания самого большого пятна размытия, которое невозможно отличить от точки. Объектив может точно фокусировать объекты только на одном расстоянии; объекты на других расстояниях расфокусированный. Точки расфокусированного объекта отображаются как размытие пятен а не очки; чем дальше объект находится от плоскости фокуса, тем больше размер пятна размытия. Такое пятно размытия имеет ту же форму, что и апертура объектива, но для простоты обычно рассматривается как круглое. На практике объекты, находящиеся на значительно разном расстоянии от камеры, все еще могут казаться резкими (Луч 2000, 50); диапазон расстояний до объекта, на котором объекты кажутся резкими, - это глубина резкости («DoF»). Общим критерием «приемлемой резкости» конечного изображения (например, отпечатка, проекционного экрана или электронного дисплея) является то, что пятно размытия нельзя отличить от точки.

В несовершенном объективе L, все лучи не проходят через точку фокусировки. Самый маленький круг, который они проходят C называется кругом наименьшего замешательства.

2. Для описания пятна размытия, достигаемого объективом, при его наилучшей фокусировке или в более общем плане, Признавая, что настоящие линзы не фокусируют все лучи идеально даже в самых лучших условиях, термин круг наименьшего замешательства часто используется для устранения самого маленького пятна размытия, которое может создать объектив (Луч 2002, 89 ), например, путем выбора наилучшего положения фокуса, обеспечивающего хороший компромисс между различными эффективными фокусные расстояния различных зон линз из-за сферических или других аберрации. Период, термин круг замешательства применяется в более общем смысле к размеру пятна не в фокусе, на которое объектив отображает точку объекта. Дифракция эффекты от волновой оптики и конечного отверстие линзы определить круг наименьшего затруднения;^[1] более общее использование «круга нерезкости» для точек, не находящихся в фокусе, может быть вычислено исключительно с точки зрения лучевой (геометрической) оптики.^[2]

В идеализированной лучевой оптике, где предполагается, что лучи сходятся в точку, когда они идеально сфокусированы, форма пятна размытия расфокусировки от линзы с круглой апертурой представляет собой круг света с резкими краями. Более общее пятно размытия имеет мягкие края из-за дифракции и аберраций (Стоксет 1969, 1317; Мерклингер 1992, 45–46), и может быть некруглым из-за формы апертуры. Следовательно, чтобы иметь смысл, необходимо тщательно определить понятие диаметра. В подходящих определениях часто используется понятие окруженная энергия, доля полной оптической энергии пятна в пределах указанного диаметра. Значения доли (например, 80%, 90%) меняются в зависимости от области применения.

Предел диаметра круга нерезкости в фотографии

В фотография, предел диаметра круга нерезкости («предел CoC» или «критерий CoC») часто определяется как самое большое пятно размытия, которое все равно будет восприниматься человеческим глазом как точка при просмотре на конечном изображении со стандартного расстояния просмотра. . Предел CoC может быть указан на конечном изображении (например, отпечатке) или на исходном изображении (на пленке или датчике изображения).

При таком определении предел CoC в исходном изображении (изображение на пленке или электронном датчике) может быть установлен на основе нескольких факторов:

1. Острота зрения. Для большинства людей самое близкое удобное расстояние просмотра, называемое на близком расстоянии для четкого зрения (Луч 2000, 52), составляет примерно 25 см. На таком расстоянии человек с хорошим зрением обычно может различить Разрешение изображения 5 пар линий на миллиметр (lp / мм), что эквивалентно CoC 0,2 мм в окончательном изображении.
2. Условия просмотра. Если конечное изображение просматривается на расстоянии примерно 25 см, часто подходит значение CoC конечного изображения 0,2 мм. Комфортным расстоянием просмотра является также такое, при котором угол обзора составляет примерно 60 ° (Луч 2000, 52); на расстоянии 25 см это соответствует примерно 30 см, примерно по диагонали изображения размером 8 ″ × 10 ″ (бумага формата A4 составляет ~ 8 дюймов × 11 ″). Часто бывает разумным предположить, что для всего изображения При просмотре окончательное изображение размером более 8 ″ × 10 ″ будет просматриваться на расстоянии, соответственно, более 25 см, и для которого может быть приемлем более крупный CoC; тогда CoC исходного изображения будет таким же, как определенное из стандартного финального изображения. -размер изображения и расстояние просмотра.Но если конечное изображение большего размера будет просматриваться на нормальном расстоянии 25 см, потребуется меньший ЦП исходного изображения для обеспечения приемлемой резкости.
3. Увеличение исходного изображения до конечного изображения. Если нет увеличения (например, контактный отпечаток 8×10 исходное изображение), CoC для исходного изображения такой же, как и в окончательном изображении. Но если, например, размер исходного изображения 35 мм по длине увеличен до 25 см (10 дюймов), увеличение составит примерно 7 ×, а CoC для исходного изображения составит 0,2 мм / 7 или 0,029 мм.

Общие значения для ограничения CoC могут не применяться, если условия воспроизведения или просмотра значительно отличаются от тех, которые предполагались при определении этих значений. Если исходное изображение будет увеличено сильнее или будет рассматриваться с более близкого расстояния, потребуется меньший CoC. Все три фактора, указанные выше, учитываются по этой формуле:

CoC в мм = (расстояние просмотра см / 25 см) / (желаемое разрешение конечного изображения в lp / мм для расстояния просмотра 25 см) / увеличение

Например, для поддержки разрешения конечного изображения, эквивалентного 5 lp / мм для расстояния просмотра 25 см, когда ожидаемое расстояние просмотра составляет 50 см, а ожидаемое увеличение - 8:

CoC = (50/25) / 5/8 = 0,05 мм

Поскольку размер окончательного изображения обычно не известен во время фотосъемки, принято принимать стандартный размер, такой как ширина 25 см, наряду с обычным ЦС конечного изображения 0,2 мм, что составляет 1/1250 от ширина изображения. Также обычно используются условные обозначения диагональной меры. DoF, вычисленный с использованием этих условных обозначений, необходимо будет скорректировать, если исходное изображение обрезано перед увеличением до конечного размера изображения, или если размер и предположения относительно просмотра изменены.

Для полнокадрового формата 35 мм (24 мм × 36 мм, диагональ 43 мм) широко используемым ограничением CoC является d/ 1500, или 0,029 мм для полнокадрового формата 35 мм, что соответствует разрешению 5 строк на миллиметр на отпечатке с диагональю 30 см. Значения 0,030 мм и 0,033 мм также являются общими для полнокадрового формата 35 мм.

Также использовались критерии, связывающие CoC с фокусным расстоянием объектива. Kodak (1972), 5) рекомендуется 2 угловые минуты ( Snellen критерий 30 циклов / градус для нормального зрения) для критического просмотра, давая CoC ≈ ж /1720, где ж - фокусное расстояние объектива. Для объектива 50 мм и полнокадрового формата 35 мм это дает CoC ≈ 0,0291 мм. Этот критерий, очевидно, предполагал, что конечное изображение будет рассматриваться с «правильной перспективы» расстояния (т.е. угол обзора будет таким же, как и у исходного изображения):

Расстояние просмотра = фокусное расстояние объектива × увеличение

Однако изображения редко просматриваются на «правильном» расстоянии; зритель обычно не знает фокусного расстояния снимающего объектива, а «правильное» расстояние может быть слишком коротким или длинным. Следовательно, критерии, основанные на фокусном расстоянии объектива, как правило, уступили место критериям (таким как d/ 1500), связанных с форматом камеры.

Если изображение просматривается на средстве отображения с низким разрешением, таком как монитор компьютера, обнаруживаемость размытия будет ограничиваться средой отображения, а не человеческим зрением. Например, оптическое размытие будет труднее обнаружить в 8 Изображение размером ″ × 10 ″ отображается на мониторе компьютера, чем на отпечатке размером 8 ″ × 10 ″ того же исходного изображения, просматриваемого с того же расстояния. Если изображение должно просматриваться только на устройстве с низким разрешением, может потребоваться более крупный CoC ; однако, если изображение может быть просмотрено на носителе с высоким разрешением, таком как печать, критерии, описанные выше, будут иметь преимущественную силу.

Формулы глубины резкости, полученные из геометрическая оптика подразумевают, что любая произвольная глубина резкости может быть достигнута с помощью достаточно маленького CoC. Потому что дифракция Однако это не совсем так. Использование меньшего CoC требует увеличения линзы f-число для достижения той же глубины резкости, и если объектив остановлен на достаточное расстояние, уменьшение размытия при расфокусировке компенсируется увеличением размытия из-за дифракции. Увидеть Глубина резкости статья для более подробного обсуждения.

Предел диаметра круга нерезкости на основе d/1500

Формат изображения	Размер кадра[3]	CoC
Малый формат
1-дюймовый сенсор (Nikon 1, Sony RX10, Sony RX100)	8,8 мм × 13,2 мм	0,011 мм
Система четырех третей	13,5 мм × 18 мм	0,015 мм
APS-C[4]	15,0 мм × 22,5 мм	0,018 мм
Canon APS-C	14,8 мм × 22,2 мм	0,018 мм
APS-C Nikon / Pentax / Sony	15,7 мм × 23,6 мм	0,019 мм
Canon APS-H	19,0 мм × 28,7 мм	0,023 мм
35 мм	24 мм × 36 мм	0,029 мм
Средний формат
645 (6×4.5)	56 мм × 42 мм	0,047 мм
6×6	56 мм × 56 мм	0,053 мм
6×7	56 мм × 69 мм	0,059 мм
6×9	56 мм × 84 мм	0,067 мм
6×12	56 мм × 112 мм	0,083 мм
6×17	56 мм × 168 мм	0,12 мм
Большой формат
4×5	102 мм × 127 мм	0,11 мм
5×7	127 мм × 178 мм	0,15 мм
8×10	203 мм × 254 мм	0,22 мм

Регулировка диаметра кружка нерезкости для шкалы DoF объектива

В ж-число, определенное по шкале DoF объектива, может быть скорректировано для отражения CoC, отличного от того, на котором основана шкала DoF. Это показано в Глубина резкости статья, которая

${\displaystyle \mathrm {DoF} ={\frac {2Nc\left(m+1\right)}{m^{2}-\left({\frac {Nc}{f}}\right)^{2}}}\,,}$

где N это объектив ж-номер, c это CoC, м - увеличение, а ж - фокусное расстояние объектива. Поскольку ж-число и CoC встречаются только как продукт Nc, увеличение одного эквивалентно соответствующему уменьшению другого, и наоборот. Например, если известно, что шкала глубины резкости объектива основана на CoC 0,035 мм, а фактические условия требуют CoC 0,025 мм, CoC необходимо уменьшить в 1 раз. 0.035 / 0.025 = 1.4; этого можно добиться, увеличив ж-число определяется по шкале глубины резкости с тем же коэффициентом, или около 1 ступени, поэтому линзу можно просто закрыть на 1 ступень от значения, указанного на шкале.

Такой же подход обычно можно использовать с калькулятором глубины резкости на камере обзора.

Определение диаметра круга нерезкости по объектному полю

Линза и диаграмма лучей для расчета диаметра кружка нерезкости c для объекта, не в фокусе, на расстоянии S₂ когда камера сфокусирована на S₁. Вспомогательный круг размытия C в плоскости объекта (пунктирная линия) упрощает расчет.

Ранний расчет диаметра CoC («нечеткость») T.H. в 1866 г.

Чтобы вычислить диаметр кружка нерезкости в плоскости изображения для объекта, находящегося не в фокусе, один из методов состоит в том, чтобы сначала вычислить диаметр кружка размытия в виртуальном изображении в плоскости объекта, что просто выполняется с использованием подобных треугольников. , а затем умножьте на увеличение системы, которое вычисляется с помощью уравнения линзы.

Размытый круг диаметром C, в плоскости сфокусированного объекта на расстоянии S₁, представляет собой несфокусированное виртуальное изображение объекта на расстоянии S₂ как показано на схеме. Это зависит только от этих расстояний и диаметра отверстия. А, через подобные треугольники, независимо от фокусного расстояния объектива:

${\displaystyle C=A{|S_{2}-S_{1}| \over S_{2}}\,.}$

Круг нерезкости в плоскости изображения получается путем умножения на увеличение м:

${\displaystyle c=Cm\,,}$

где увеличение м дается соотношением фокусных расстояний:

${\displaystyle m={f_{1} \over S_{1}}\,.}$

Используя уравнение линзы, мы можем решить для вспомогательной переменной ж₁:

${\displaystyle {1 \over f}={1 \over f_{1}}+{1 \over S_{1}}\,,}$

что дает

${\displaystyle f_{1}={fS_{1} \over S_{1}-f}\,.}$

и выразите увеличение через фокусное расстояние и фокусное расстояние:

${\displaystyle m={f \over S_{1}-f}\,,}$

что дает окончательный результат:

${\displaystyle c=A{|S_{2}-S_{1}| \over S_{2}}{f \over S_{1}-f}\,.}$

При желании это может быть выражено через f-число N = f / A в качестве:

${\displaystyle c={|S_{2}-S_{1}| \over S_{2}}{f^{2} \over N(S_{1}-f)}\,.}$

Эта формула точна для простого параксиальный тонкая линза или симметричная линза, в которой входной и выходной зрачки имеют диаметр А. Более сложные конструкции линз с увеличением зрачка, отличным от единицы, потребуют более сложного анализа, как описано в глубина резкости.

В более общем смысле, этот подход приводит к точному параксиальному результату для всех оптических систем, если А это вступительный ученик диаметр, расстояние до объекта измеряется от входного зрачка, а увеличение известно:

${\displaystyle c=Am{|S_{2}-S_{1}| \over S_{2}}\,.}$

Если фокусное расстояние или расстояние до объекта вне фокуса бесконечно, уравнения могут быть оценены в пределе. Для бесконечного расстояния фокусировки:

${\displaystyle c={fA \over S_{2}}={f^{2} \over NS_{2}}\,.}$

И для размытого круга объекта на бесконечности при конечном расстоянии фокусировки:

${\displaystyle c={fA \over S_{1}-f}={f^{2} \over N(S_{1}-f)}\,.}$

Если c значение фиксировано как круг предельного диаметра нерезкости, любой из них может быть решен для расстояния до объекта, чтобы получить гиперфокальное расстояние, с примерно эквивалентными результатами.

История

Генри Коддингтон 1829

Прежде чем применить его к фотографии, понятие круга нерезкости применялось к оптическим инструментам, таким как телескопы. Коддингтон (1829 г., 54 ) количественно оценивает как круг наименьшего замешательства и наименьший круг замешательства для сферической отражающей поверхности.

Это можно рассматривать как ближайший подход к простому фокусу и называть круг наименьшего замешательства.

Общество распространения полезных знаний 1832 г.

В Общество распространения полезных знаний (1832 г.), п.11 ) Ошибка harvtxt: нет цели: CITEREFSociety_for_the_Diffusion_of_Useful_Knowledge1832 (Помогите) применил его к аберрациям третьего порядка:

Эта сферическая аберрация приводит к нечеткости зрения, поскольку каждая математическая точка объекта помещается в небольшое пятно на его изображении; какие пятна, смешиваясь друг с другом, сбивают с толку целое. Диаметр этого круга нерезкости в фокусе центральных лучей F, на который распространяется каждая точка, будет L K (рис. 17.); а когда апертура отражателя умеренная, она равна кубу апертуры, деленному на квадрат радиуса (...): этот круг называется аберрацией широты.

T.H. 1866 г.

Вычисления по кругу неясности: один из первых предшественников глубина резкости расчеты TH (1866 г., п. 138) Ошибка harvtxt: цель отсутствует: CITEREFTH1866 (Помогите) вычисление диаметра кружка нерезкости на расстоянии до объекта для объектива, сфокусированного на бесконечность; на эту статью указал фон Рор (1899). Формула, которую он придумал для определения того, что он называет «нечеткостью», эквивалентна, говоря современным языком,

${\displaystyle c={fA \over S}}$

для фокусного расстояния ${\displaystyle f}$, диаметр апертуры А, и расстояние до объекта S. Но он не переворачивает это, чтобы найти S соответствующий данному c критерий (т.е. он не решает гиперфокальное расстояние ), и он не рассматривает возможность фокусировки на любом другом расстоянии, кроме бесконечности.

Наконец он замечает, что «длиннофокусные линзы обычно имеют большую диафрагму, чем короткие, и на этом счете иметь меньшую глубину резкости »[выделено курсивом].

Даллмейер и Эбни

Даллмейер (1892 г., п. 24) Ошибка harvtxt: нет цели: CITEREFDallmeyer1892 (Помогите), в расширенном переиздании его отца Джон Генри Даллмейер 1874 г. (Даллмейер 1874 ) ошибка harv: цель отсутствует: CITEREFDallmeyer1874 (Помогите) брошюра О выборе и использовании фотообъективов (в материале, которого нет в издании 1874 года и который, по-видимому, был добавлен из статьи J.H.D. «Об использовании диафрагм или стопоров» неизвестной даты), говорится:

Таким образом, каждая точка объекта не в фокусе представлена ​​на изображении диском или кружком нерезкости, размер которого пропорционален апертуре по отношению к фокусу используемого объектива. Если точка в объекте находится не в фокусе на 1/100 дюйма, она будет представлена ​​кружком нерезкости, размер которого составляет 1/100 часть апертуры объектива.

Последнее утверждение явно неверно или неверно, поскольку оно отличается от коэффициента фокусного расстояния (фокусного расстояния). Он продолжает:

и когда круги смятения достаточно малы, глаз не видит их как таковых; тогда они видны только как точки, и изображение кажется резким. На обычном расстоянии видимости, от двенадцати до пятнадцати дюймов, круги нерезкости рассматриваются как точки, если их угол не превышает одной угловой минуты, или примерно, если они не превышают 1/100 угловой минуты. дюйм в диаметре.

Численно 1/100 дюйма на расстоянии от 12 до 15 дюймов ближе к двум угловым минутам. Этот выбор предела COC остается (для крупного шрифта) наиболее широко используемым даже сегодня. Эбни (1881 г., стр.207–08 ) Ошибка harvtxt: нет цели: CITEREFAbney1881 (Помогите) использует аналогичный подход, основанный на остроте зрения в одну угловую минуту, и выбирает кружок нерезкости 0,025 см для просмотра с расстояния от 40 до 50 см, по существу делая ту же ошибку с коэффициентом два в метрических единицах. Неясно, Эбни или Даллмейер ранее устанавливали стандарт КОК.

Стена 1889 г.

Обычный предел COC 1/100 дюйма был применен к размытию, кроме размытия при расфокусировке. Например, Стена (1889 г., 92 ) говорит:

Чтобы узнать, насколько быстро должен действовать затвор, чтобы привести объект в движение, в котором может быть нечеткий круг менее 1/100 дюйма. в диаметре, разделите расстояние до объекта на 100-кратное расстояние фокусировки объектива и разделите скорость движения объекта в дюймах в секунду на результаты, когда у вас самая большая продолжительность экспозиции в долях секунды.

Смотрите также

• Диск Эйри
• Астигматизм
• Боке
• Хроматическая аберрация
• Аберрация расфокусировки
• Фокальное облако
• Сфера (оптика)
• Точечный источник света
• Функция распределения точки
• Формула Цейса

Примечания

1. Ж.-А. Бералдин; и другие. (2006). «Виртуальная реконструкция объектов наследия: возможности и вызовы, создаваемые 3D-технологиями». В Маносе Балтсавиасе; Армин Груэн; Люк Ван Гул; Мария Патераки (ред.). Запись, моделирование и визуализация культурного наследия. Тейлор и Фрэнсис. п. 145. ISBN  978-0-415-39208-2.
2. Уолтер Балкли Ковентри (1901). Техника ручной камеры. Sands & Co. стр. 9.
3. Размер кадра - средний для фотоаппаратов, которые делают фотографии этого формата. Например, не все камеры 6x7 снимают кадры, которые точно соответствуют 56 мм × 69 мм. Если требуется такой уровень точности, сверьтесь со спецификациями конкретной камеры.
4. “APS-C »- распространенный формат цифровых SLR. Размеры у разных производителей незначительно отличаются; например, формат Canon APS-C номинально 15,0 мм × 22,5 мм, а Nikon Формат DX номинально 16 мм × 24 мм. Точные размеры иногда незначительно отличаются между моделями одного и того же номинального формата от одного производителя.

использованная литература

• Эбни, сэр Уильям де Вивелсли. 1881. Трактат о фотографии. Лондон: Longmans, Green and Co.
• Коддингтон, Генри. 1829. Трактат об отражении и преломлении света: часть I. системы оптики. Кембридж: Дж. Смит.
• Даллмейер, Джон Генри. 1874. О выборе и использовании фотообъективов. Нью-Йорк: Э. и Х. Энтони и Ко.
• Даллмейер, Томас Р.. 1892. О выборе и использовании фотообъективов. Лондон: Дж. Питчер.
• Компания Eastman Kodak. 1972 г. Оптические формулы и их применение, Публикация Kodak № AA-26, Ред. 11-72-BX. Рочестер, Нью-Йорк: компания Eastman Kodak.
• Kodak. Увидеть Компания Eastman Kodak.
• Мерклингер, Гарольд М. 1992. Входы и выходы фокусировки: альтернативный способ оценки глубины резкости и резкости фотографического изображения. Версия 1.0.3. Бедфорд, Новая Шотландия: Seaboard Printing Limited. ISBN  0-9695025-0-8. Версия 1.03e доступна в PDF в http://www.trenholm.org/hmmerk/.
• Рэй, Сидни Ф. 2000. Геометрия формирования изображения. В Руководство по фотографии: фотография и цифровая обработка изображений, 9 изд. Эд. Ральф Э. Якобсон, Сидней Ф. Рей, Джеффри Г. Аттеридж и Норман Р. Аксфорд. Оксфорд: Focal Press. ISBN  0-240-51574-9
• Рэй, Сидни Ф. 2002. Прикладная фотографическая оптика, 3-е изд. Оксфорд: Focal Press. ISBN  0-240-51540-4
• Общество распространения полезных знаний. 1832. Естественная философия: с объяснением научных терминов и указателем. Лондон: Болдуин и Крадок, Патерностер-Роу.
• Стоксет, Пер А. 1969. Свойства расфокусированной оптической системы. Журнал Оптического общества Америки 59:10, октябрь 1969 г.
• T.H. [псевд.]. 1866 г. «Долгий и короткий фокус». Британский журнал фотографии 13.
• фон Рор, Мориц. 1899. Photographische Objektiv. Берлин: Verlag Julius Springer.
• Уолл, Эдвард Джон. 1889 г. Словарь по фотографии для фотографа-любителя и профессионального фотографа. Нью-Йорк: Э. и Х. Т. Энтони и Ко.

внешняя ссылка

• Круги путаницы для цифровых фотоаппаратов - DOFMaster
• Глубина резкости по глубине (PDF) - включает обсуждение критериев круга нечеткости
• Что такое «круг замешательства» - ƒ / Calc руководство