Центральный угол - Central angle

Угол AOB - это центральный угол

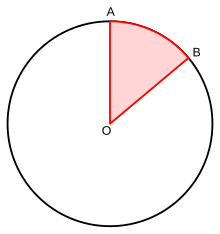
А центральный угол является угол вершина (вершина) которого является центром O окружности, а ноги (стороны) - радиусы пересекая круг в двух различных точках A и B. Центральные углы равны поданный по дуга между этими двумя точками и длина дуги - центральный угол круга радиуса один (измеряется в радианы ).^[1] Центральный угол также известен как дуга. угловое расстояние.

Размер центрального угла Θ является 0 ° <Θ <360 ° или же 0 <Θ <2π (радианы). При определении или рисовании центрального угла в дополнение к указанию точек А и B, необходимо указать, является ли определяемый угол углом выпуклости (<180 °) или углом отражения (> 180 °). Точно так же необходимо указать, является ли движение от точки А В точку B по часовой стрелке или против часовой стрелки.

Формулы

Если точки пересечения А и B ног уголка с кругом образуют диаметр, тогда Θ = 180 ° это прямой угол. (В радианах Θ = π.)

Позволять L быть малая дуга круга между точками А и B, и разреши р быть радиус круга.^[2]

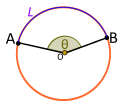Центральный угол. Выпуклый. Подчеркивается малой дугой L

Если центральный угол Θ поддерживается L, тогда

${\displaystyle 0^{\circ }<\Theta <180^{\circ }\,,\,\,\Theta =\left({\frac {180L}{\pi R}}\right)^{\circ }={\frac {L}{R}}.}$

Доказательство (для степеней): длина окружности круга с радиусом р является 2πр, а малая дуга L это (Θ/360°) пропорциональная часть всей окружности (см. дуга ). Так:

${\displaystyle L={\frac {\Theta }{360^{\circ }}}\cdot 2\pi R\,\Rightarrow \,\Theta =\left({\frac {180L}{\pi R}}\right)^{\circ }.}$

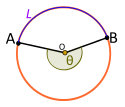Центральный угол. Рефлекс. Является нет представлен L

Доказательство (для радианов): длина окружности круга с радиусом р является 2πр, а малая дуга L это (Θ/2π) пропорциональная часть всей окружности (см. дуга ). Так

${\displaystyle L={\frac {\Theta }{2\pi }}\cdot 2\pi R\,\Rightarrow \,\Theta ={\frac {L}{R}}.}$

Если центральный угол Θ является нет подчинено малой дуге L, тогда Θ угол отражения и

${\displaystyle 180^{\circ }<\Theta <360^{\circ }\,,\,\,\Theta =\left(360-{\frac {180L}{\pi R}}\right)^{\circ }=2\pi -{\frac {L}{R}}.}$

Если касательная в А и касательная в B пересекаются во внешней точке п, затем обозначив центр как О, углы ∠BOA (выпуклый) и ∠BPA находятся дополнительный (сумма до 180 °).

Центральный угол правильного многоугольника

А правильный многоугольник с п стороны имеет описанный круг на котором лежат все его вершины, а центр круга также является центром многоугольника. Центральный угол правильного многоугольника образован в центре радиусами двух соседних вершин. Мера этого угла равна ${\displaystyle 2\pi /n.}$

Смотрите также

• Вписанный угол
• Навигация по большому кругу

Рекомендации

1. Clapham, C .; Николсон, Дж. (2009). «Оксфордский краткий математический словарь, центральный угол» (PDF). Эддисон-Уэсли. п. 122. Получено 30 декабря, 2013.
2. «Центральный угол (окружности)». Открытый справочник по математике. 2009 г.. Получено 30 декабря, 2013. интерактивный

внешняя ссылка

• «Центральный угол (окружности)». Открытый справочник по математике. 2009 г.. Получено 30 декабря, 2013. интерактивный
• "Теорема о центральном угле". Открытый справочник по математике. 2009 г.. Получено 30 декабря, 2013. интерактивный
• Вписанные и центральные углы по кругу