Безфононная линия и фононная боковая полоса - Zero-phonon line and phonon sideband

Рисунок 1. Схематическое изображение формы линии поглощения электронного возбуждения. Узкая составляющая на частоте ω ′ является бесфононной линией, а более широкая особенность - фононной боковой полосой. При излучении относительные положения двух компонентов отражаются относительно центра бесфононной линии в точке ω '.

В бесфононная линия и фонон боковая полоса вместе составляют линия форма отдельных светопоглощающих и излучающих молекул (хромофоры ) встроены в прозрачную твердую матрицу. Когда матрица-хозяин содержит много хромофоров, каждый будет давать нулевойфонон линии и фононной боковой полосы к поглощению и излучению спектры. Спектры, возникающие из набора идентичных хромофоров в матрице, считаются неоднородно расширенными, потому что каждый хромофор окружен несколько разным матричным окружением, которое изменяет энергию, необходимую для электронного перехода. Таким образом, при неоднородном распределении хромофоров отдельные бесфононные линии и положения боковых полос фононов смещены и перекрываются.

На рис. 1 показана типичная форма линий электронных переходов отдельных хромофоров в твердой матрице. Бесфононная линия расположена в точке частота ω ’определяется внутренней разницей в уровнях энергии между основным и возбужденным состояниями, а также локальной средой. Боковая полоса фононов смещается в сторону более высокой частоты поглощения и более низкой частоты флуоресценции. Частотный зазор Δ между бесфононной линией и пиком боковой фононной полосы определяется соотношением Принципы Франка – Кондона.

Распределение интенсивности между бесфононной линией и боковой фононной полосой сильно зависит от температуры. При комнатной температуре тепловой энергии достаточно, чтобы возбудить много фононов, и вероятность бесфононного перехода близка к нулю. Для органических хромофоров в органических матрицах вероятность бесфононного электронного перехода становится вероятной только ниже 40 кельвины, но зависит также от силы связи между хромофором и решеткой хозяина.

Энергетическая диаграмма

Фигура 2. Энергетическая диаграмма электронного перехода с фононной связью по конфигурационной координате q _я, а нормальный режим решетки. Стрелки вверх показывают поглощение без фононов и с тремя фононами. Стрелки вниз представляют симметричный процесс излучения.

Рисунок 3. Представление трех нормальных мод решетки (я, j, k) и то, как их интенсивности объединяются на бесфононной частоте, но распределяются внутри фононной боковой полосы из-за их различных характерных частот гармонических осцилляторов. Ω.

Переход между земля и возбужденное состояние основан на Принцип Франка – Кондона, что электронный переход происходит очень быстро по сравнению с движением в решетке. Затем энергетические переходы могут быть обозначены вертикальными стрелками между основным и возбужденным состояниями, то есть движение по конфигурационным координатам во время перехода отсутствует. Рисунок 2 представляет собой энергетическую диаграмму для интерпретации поглощения и излучения с фононами и без них в терминах конфигурационной координаты q_я. Энергетические переходы происходят на самом низком фононном уровне энергии электронных состояний. Как показано на рисунке, наибольшее перекрытие волновых функций (и, следовательно, наибольшая вероятность перехода) происходит, когда фотон энергия равна разности энергий между двумя электронными состояниями (E₁ – E₀) плюс три кванты решетки я колебательная энергия (${\displaystyle \hbar \Omega _{i}}$). Этот трехфононный переход отражается в излучении, когда возбужденное состояние быстро распадается до нулевого уровня колебаний решетки посредством безызлучательного процесса, а оттуда в основное состояние посредством испускания фотонов. Бесфононный переход изображается как имеющий меньшее перекрытие волновых функций и, следовательно, меньшую вероятность перехода.

В дополнение к предположению Франка-Кондона обычно предполагаются три других приближения, которые неявно присутствуют на рисунках. Во-первых, каждая колебательная мода решетки хорошо описывается квантовый гармонический осциллятор. Это приближение подразумевается в параболический форма потенциальных ям, показанных на рис. 2, и одинаковое энергетическое расстояние между уровнями энергии фононов. Второе приближение состоит в том, что возбуждается только низшее (нулевое) колебание решетки. Это называется приближением низких температур и означает, что электронные переходы не происходят ни на одном из более высоких фононных уровней. Третье приближение заключается в том, что взаимодействие между хромофором и решеткой одинаково как в основном, так и в возбужденном состоянии. В частности, потенциал гармонического осциллятора одинаков в обоих состояниях. Это приближение, называемое линейной связью, представлено на рисунке 2 двумя параболическими потенциалами одинаковой формы и равноудаленными уровнями энергии фононов как в основном, так и в возбужденном состояниях.

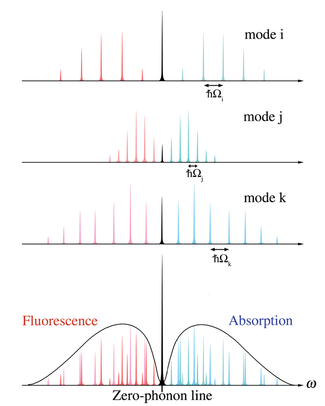
Сила бесфононного перехода возникает в суперпозиции всех мод решетки. Каждая решетка Режим м имеет характерную частоту колебаний Ω_м что приводит к разнице энергий фононов ${\displaystyle \hbar \Omega _{m}}$. Когда вероятности переходов для всех мод суммируются, бесфононные переходы всегда складываются в электронном начале координат (E₁ – E₀), а переходы с фононами дают вклад в распределение энергий. Рисунок 3 иллюстрирует суперпозицию вероятностей переходов нескольких мод решетки. Вклады фононных переходов от всех мод решетки составляют фононную боковую полосу.

Частотное разделение между максимумами боковых полос фононов поглощения и флуоресценции является фононным вкладом в Смена Стокса.

Форма линии

Форма бесфононной линии Лоренциан шириной, определяемой временем жизни возбужденного состояния Т₁₀ согласно Гейзенбергу принцип неопределенности. Без влияния решетки естественная ширина линии (полная ширина на половине высоты) хромофора составляет γ₀ = 1/Т₁₀ . Решетка уменьшает время жизни возбужденного состояния за счет введения безызлучательных механизмов распада. В абсолютный ноль время жизни возбужденного состояния под влиянием решетки равно Т₁. Выше абсолютного нуля тепловые движения вносят случайные возмущения в локальное окружение хромофоров. Эти возмущения сдвигают энергию электронного перехода, вызывая температурное уширение ширины линии. Тогда измеренная ширина нулевой фононной линии одного хромофора, однородная ширина линии, равна γ_час(Т) ≥ 1/Т₁ .

Форма линии фононной боковой полосы такая же, как у распределение Пуассона поскольку он выражает дискретное количество событий, электронных переходов с фононами, в течение периода времени. При более высоких температурах или когда хромофор сильно взаимодействует с матрицей, вероятность появления многофононности высока, а боковая полоса фононов приближается к Гауссово распределение.

Распределение интенсивности между бесфононной линией и фононной боковой полосой характеризуется Фактор Дебая-Валлера α.

Аналогия с эффектом Мёссбауэра

Бесфононная линия является оптическим аналогом Мёссбауэровские линии, которые возникают в результате безоткатного излучения или поглощения гамма излучение из ядер атомов, связанных в твердую матрицу. В случае оптической бесфононной линии положение хромофора является физическим параметром, который может быть нарушен, тогда как при гамма-переходе импульсы атомов может быть изменено. С технической точки зрения ключ к аналогии - симметрия между положением и импульсом в Гамильтониан из квантовый гармонический осциллятор. И положение, и импульс вносят одинаковый (квадратичный) вклад в общую энергию.

Смотрите также

• Фонон
• Эффект Мёссбауэра
• Матрица Шпольского

Рекомендации

• Friedrich, J. J .; Д. Хаарер (1984). "Фотохимическое горение дырок: спектроскопическое исследование релаксационных процессов в полимерах и стеклах". Angewandte Chemie International Edition на английском языке. 23 (2): 113–140. Дои:10.1002 / anie.198401131.
• Сильд, О. (1988). Бесфононные линии и спектральное выжигание дырок в спектроскопии и фотохимии. Берлин: Springer-Verlag. ISBN  978-3-540-19214-5.

внешняя ссылка

• Сайт Александра Ребана в Государственном университете Монтаны, Бозман
• Гиперфизика: молекулярные спектры