Усеченная икосододекаэдрическая призма - Truncated icosidodecahedral prism

Усеченная икосододекаэдрическая призма
Диаграмма Шлегеля
Тип	Призматический однородный 4-многогранник
Единый индекс	63
Символ Шлефли	т0,1,2,3{3,5,2} или tr {3,5} × {}
Кокстер-Дынкин
Клетки	64 всего: 2 4.6.10 30 4.4.4 20 4.4.6 12 4.4.10
Лица	Всего 304: 240 {4} 40 {6} 24 {5}
Края	480
Вершины	240
Фигура вершины	Нерегулярный тетраэдр
Группа симметрии	[5,3,2], заказ 240
Характеристики	выпуклый

Сеть

В геометрия, а усеченная икосододекаэдрическая призма или же большая ромбоикосододекаэдрическая призма выпуклый униформа 4-многогранник (четырехмерный многогранник ).

Это один из 18 выпуклых однородные многогранные призмы создан с использованием униформы призмы соединить пары Платоновы тела или же Архимедовы тела в параллели гиперплоскости.

Альтернативные названия

• Усеченная икосододекаэдрическая диадическая призма (Норман В. Джонсон)
• Griddip (Джонатан Бауэрс: для большой ромбикосододекаэдрической призмы / гиперпризмы)
• Большая ромбикосододекаэдрическая призма / гиперпризма

Связанные многогранники

А полная курносая додекаэдрическая антипризма или же всенаправленная додекаэдрическая антипризма можно определить как чередование усеченной икосододекаэдрической призмы, представленной ht_0,1,2,3{5,3,2} или , хотя его нельзя построить как равномерный 4-многогранник. В нем 184 ячейки: 2 курносые додекаэдры связаны 30 тетраэдры, 12 пятиугольные антипризмы, и 20 октаэдры, с 120 тетраэдры в чередующихся промежутках. У него 120 вершин, 480 ребер и 544 грани (24 пятиугольника и 40 + 480 треугольников). Имеет [5,3,2]⁺ симметрия, порядок 120.

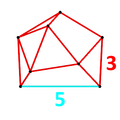
Фигура вершины для всенаправленная додекаэдрическая антипризма

внешняя ссылка

• 6. Выпуклая однородная призматическая полихора - Модель 63., Георгий Ольшевский.
• Клитцинг, Ричард. "4D однородные многогранники (полихоры) x x3o5x - griddip".