Тетромино - Tetromino

5 бесплатных тетромино

А тетромино представляет собой геометрическую фигуру, состоящую из четырех квадраты, связаны ортогонально (т.е. по краям, а не по углам).[1][2] Это, как домино и пентамино, это особый тип полимино. Соответствующие поликуб, называется тетракуб, представляет собой геометрическую фигуру, состоящую из четырех кубики соединены ортогонально.

Тетромино широко используется в видео игра Тетрис, который называет их тетримино.[3] Тетромино, используемое в игре, - это, в частности, одностороннее тетромино.

Тетромино

Бесплатные тетромино

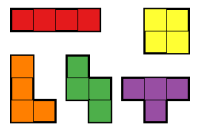
Полиомино образованы соединением единичных квадратов по краям. А бесплатное полимино является полимино, рассмотренным с точностью до соответствие. То есть два свободных полиомино одинаковы, если есть комбинация переводы, вращения, и размышления что превращает одно в другое. Свободное тетромино - это свободное полимино, состоящее из четырех квадратов. Есть пять бесплатных тетромино.

Свободные тетромино обладают следующей симметрией:

  • Прямая: вертикальная и горизонтальная симметрия отражения и две точки симметрии вращения
  • Квадрат: вертикальная и горизонтальная симметрия отражения и четыре точки симметрии вращения
  • T: только симметрия вертикального отражения
  • L: нет симметрии
  • Перекос: только две точки вращательной симметрии
"прямое тетромино"
"квадратное тетромино"
«Т-тетромино»
«L-тетромино»
"косой тетромино"










Одностороннее тетромино

Односторонние тетромино - это тетромино, которые можно перемещать и вращать, но не отражать. Они используются и в основном связаны с Тетрис. Есть семь различных односторонних тетромино. Эти тетромино названы по букве алфавита, на которую они наиболее похожи. Тетромино «I», «O» и «T» обладают отражательной симметрией, поэтому не имеет значения, считаются ли они свободными тетромино или односторонними тетромино. Остальные четыре тетромино, «J», «L», «S» и «Z», демонстрируют явление, называемое хиральность. J и L - это отражение друг друга, а S и Z - отражение друг друга.

Как свободное тетромино, J эквивалентно L, а S эквивалентно Z. Но в двух измерениях и без отражений невозможно преобразовать J в L или S в Z.

я
О
Т
J
L
S
Z









Фиксированные тетромино

Фиксированные тетромино допускают только перенос, а не вращение или отражение. Есть два различных фиксированных I-тетромино, четыре J, четыре L, один O, два S, четыре T и два Z, всего 19 фиксированных тетромино:













Замощение прямоугольника

Заполнение прямоугольника одним набором тетромино

Одиночный набор свободных тетромино или односторонних тетромино не может поместиться в прямоугольник. Это можно показать с помощью доказательства, аналогичного аргументу изуродованной шахматной доски. Прямоугольник 5х4 с шахматным рисунком состоит из 20 квадратов, содержащих 10 светлых квадратов и 10 темных квадратов, но полный набор бесплатных тетромино состоит из 11 темных и 9 светлых квадратов. Это связано с тем, что T-тетромино имеет 3 темных квадрата и один светлый квадрат, в то время как все остальные тетромино имеют по 2 темных квадрата и 2 светлых квадрата. Точно так же прямоугольник 7x4 состоит из 28 квадратов, содержащих по 14 квадратов каждого оттенка, а набор односторонних тетромино состоит из 15 темных квадратов и 13 светлых квадратов. Таким образом, любое нечетное количество наборов любого типа не может поместиться в прямоугольник. Кроме того, 19 фиксированных тетромино не могут поместиться в прямоугольник 4x19. Это было обнаружено исчерпанием всех возможностей компьютерного поиска.

Свободное тетромино (левая часть линии) состоит из 11 темных и 9 светлых квадратов.
Односторонние тетромино (все 7 показаны выше) имеют 15 темных квадратов и 13 светлых квадратов.
Доска 5x4 состоит из 10 квадратов каждого цвета.
Доска 7x4 имеет 14 квадратов каждого цвета.













Заполнение модифицированного прямоугольника одним набором тетромино

Однако все три набора тетромино подходят для прямоугольников с отверстиями:

  • Все 5 бесплатных тетромино помещаются в прямоугольник 7x3 с отверстием.
  • Все 7 односторонних тетромино умещаются в прямоугольник 6х5 с двумя отверстиями одного и того же «цвета шахматной доски».
  • Все 19 фиксированных тетромино помещаются в прямоугольник 11x7 с отверстием.
Бесплатные тетромино в прямоугольнике с одним отверстием
Одностороннее тетромино в прямоугольнике с двумя отверстиями
Фиксированные тетромино в прямоугольнике с одним отверстием











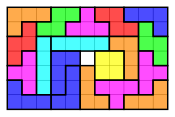
Заполнение прямоугольника двумя наборами тетромино

Два набора свободных или односторонних тетромино могут по-разному вписываться в прямоугольник, как показано ниже:

Два набора свободных тетромино в прямоугольнике 5x8
Два набора бесплатных тетромино в прямоугольнике 4х10
Два набора односторонних тетромино в прямоугольнике 8x7
Два набора односторонних тетромино в прямоугольнике 14х4












Этимология

Название «тетромино» представляет собой сочетание префикс тетра- «четверка» (от Древнегреческий τετρα-), и "домино ". Название было введено Соломон В. Голомб в 1953 г. вместе с другой номенклатурой, относящейся к полиомино.[4][1]

Наполнение коробки тетракубами

Каждому из пяти свободных тетромино соответствует тетракуб, которым является тетромино. экструдированный На одну единицу. J и L - тот же тетракуб, что и S и Z, потому что один может вращаться вокруг оси, параллельной плоскости тетромино, чтобы сформировать другой. Возможны еще три тетракуба, все они созданы путем размещения единичного куба на изогнутом трикуб:

я
"прямой тетракуб"
О
"квадратный тетракуб"
Т
«Т-тетракуб»
L
«L-тетракуб»
J то же самое, что L в 3D
S
"косой тетракуб"
Z то же самое, что и S в 3D
B
"Ответвляться"
D
"Правый винт"
F
"Левый винт"








Тетракубы можно упаковать в двухслойные трехмерные коробки несколькими способами в зависимости от размеров коробки и критериев включения. Они показаны как на графической, так и на текстовой диаграммах. Для коробок, состоящих из двух наборов одинаковых предметов, на графической диаграмме каждый набор изображен более светлым или темным оттенком того же цвета. Текстовая диаграмма показывает, что каждый набор имеет заглавную или строчную букву. На текстовой диаграмме верхний слой находится слева, а нижний слой - справа.

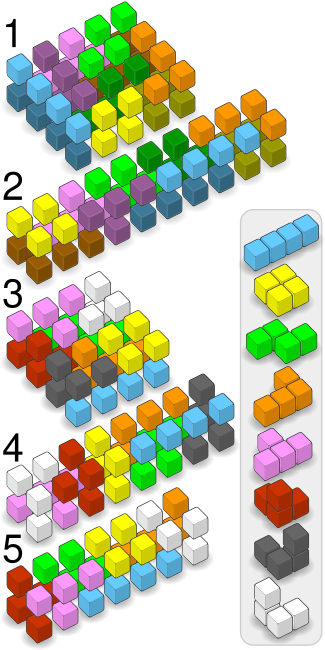
Тетромино тетракуб упаковка.svg
1.) Коробка 2x4x5, заполненная двумя наборами бесплатных тетромино: ZZT t I l TTT iL ZZ t I lllt iL zzt I oozz iL LOOI oo OO i2.) Коробка 2x2x10, заполненная двумя наборами бесплатных тетромино: LLL zz ZZTOO oozz ZZTTT lL IIII ttt OO ooiiiitll l3.) Коробка 2x4x4, заполненная одним набором всех тетракубов: FTTTFZZ BF FTBZZB BO OLDLLL DO ODDIII I4.) Коробка 2x2x8, заполненная одним набором всех тетракубов: DZZLOTTTDLLLOBF FD DZZOBTFII. части зеркального отображения удалены: LLLZZBBLCOOZZ BC IIIITBCCOOTTT

Смотрите также

Рекомендации

  1. ^ а б Голомб, Соломон В. (1994). Полимино (2-е изд.). Принстон, Нью-Джерси: Издательство Принстонского университета. ISBN  0-691-02444-8.
  2. ^ Редельмайер, Д. Хью (1981). «Подсчет полимино: еще одна атака». Дискретная математика. 36: 191–203. Дои:10.1016 / 0012-365X (81) 90237-5.
  3. ^ «О тетрисе», Tetris.com. Проверено 19 апреля 2014.
  4. ^ Дорогой, Дэвид. «Полёмино». daviddarling.info. Получено 23 мая, 2020.

внешняя ссылка