Кости Napiers - Napiers bones
Эта статья поднимает множество проблем. Пожалуйста помоги Улучши это или обсудите эти вопросы на страница обсуждения. (Узнайте, как и когда удалить эти сообщения-шаблоны) (Узнайте, как и когда удалить этот шаблон сообщения)
|

Кости Напьера это счетное устройство с ручным управлением, созданное Джон Напье из Мерчистон, Шотландия для расчет продуктов и частные номеров. Метод был основан на решеточное умножение, а также называется «рабдология», это слово придумал Нэпьер. Напье опубликовал свою версию в 1617 г. в Rabdologiæ,[1] напечатано в Эдинбург, посвященный своему покровителю Александр Сетон.
Используя таблицы умножения, встроенные в стержни, умножение можно свести к операциям сложения, а деление - к вычитаниям. Расширенное использование стержней может извлечь квадратные корни. Кости Напьера не такие, как логарифмы, с которым также связано имя Напьера, но основанные на разрезанных таблицах умножения.
В комплект устройства обычно входит основная плата с бортиком; пользователь помещает стержни Напье внутрь обода для умножения или деления. Левый край доски разделен на девять квадратов с цифрами от 1 до 9. В оригинальном дизайне Napier стержни сделаны из металла, дерева или слоновой кости и имеют квадратное поперечное сечение. На каждом стержне выгравирована таблица умножения на каждой из четырех граней. В некоторых более поздних конструкциях стержни были плоскими и имели две таблицы или только одну выгравированную на них, и были сделаны из пластика или плотного картона. Набор таких костей можно было бы вложить в переносную сумку.
Лицевая сторона стержня отмечена девятью квадратами. Каждый квадрат, кроме верхнего, делится на две половины диагональной линией от левого нижнего угла до правого верхнего. Квадраты содержат простую таблицу умножения. Первая содержит одну цифру, которую Нейпир назвал «одиночной». Остальные содержат числа, кратные единице, а именно удвоенную единицу, троекратную единицу и так далее до девятого квадрата, содержащего в девять раз больше числа в верхнем квадрате. Однозначные числа записываются в правом нижнем треугольнике, а другой треугольник остается пустым, а двузначные числа записываются цифрами по обе стороны от диагонали.
Если таблицы хранятся на односторонних стержнях, необходимо 40 стержней для умножения 4-значных чисел - поскольку числа могут иметь повторяющиеся цифры, необходимы четыре копии таблицы умножения для каждой из цифр от 0 до 9. Если используются квадратные стержни, 40 таблиц умножения могут быть нанесены на 10 стержней. Напье подробно описал схему расположения столов так, чтобы ни одна из стержней не имела двух копий одной и той же таблицы, что позволило представить каждое возможное четырехзначное число 4 из 10 стержней. Набор из 20 стержней, состоящий из двух идентичных копий 10 стержней Napier, позволяет производить вычисления с числами до восьми цифр, а набор из 30 стержней может использоваться для 12-значных чисел.
Умножение
Простейший вид умножения - числа с несколькими цифрами на число с одной цифрой - выполняется путем размещения стержней, представляющих многозначное число, в рамке напротив левого края. Ответ считывается в строке, соответствующей однозначному номеру, который отмечен слева от рамки, с небольшим добавлением, как объяснено в примерах ниже.
При умножении многозначного числа на другое многозначное число выставляется большее число на стержнях в рамке. Устройство выдает промежуточный результат для умножения на каждую цифру меньшего числа. Они записываются, а конечный результат вычисляется ручкой и бумагой.
Чтобы продемонстрировать, как использовать кости Напьера для умножения, ниже объясняются три примера возрастающей сложности.
Пример 1 - умножение на маленькое однозначное число
В первом примере вычисляется 425 × 6.
Кости Непьера для 4, 2 и 5 помещаются на доску. Кости для большего числа умножаются. В качестве примера значений, полученных из таблиц умножения, значения седьмой строки 4-й кости будут2 ⁄ 8, происходит от 7 × 4 = 28. В приведенном ниже примере для 425 × 6, кости показаны красным, желтым и синим цветом соответственно.
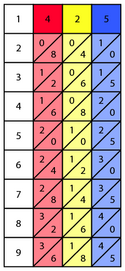
Самый левый столбец перед любой из костей может быть представлен как 1 кость, которая будет иметь пробел или ноль в верхнем левом углу, разделенные диагональной линией, поскольку 1 × 1 = 01, 1 × 2 = 02, 1 х 3 = 03и т.д. Выбирается небольшое число, обычно от 2 до 9, чтобы умножить большое число. В этом примере небольшое число, которое умножается на, равно 6. Строка, в которой находится это число, является единственной строкой, необходимой для выполнения оставшихся вычислений, и поэтому обычно изолирована от остальной части доски для ясности.

Расчет можно было начать с любого конца. Значения, разделенные вертикальными линиями, складываются для образования цифр продуктов. Последнее число, найденное в этом горизонтальном ряду костей, никогда не потребует добавления, так как оно всегда изолируется последней строкой. Он всегда находится на «своем месте» в продукте. Для остальных цифр суммируются два соседних номера костей, разделенные вертикальными линиями. В этом примере четыре цифры, поскольку есть четыре группы значений костей, разделенных линиями. Цифры продукта идут в том же порядке, в котором они рассчитываются. Помимо последней (или первой) цифры, цифры продукта будут представлять собой сумму двух значений, взятых из двух разных костей.
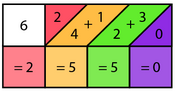
Значения костей добавляются, чтобы получить цифры продукта. Третья цифра продукта из желтой и синей костей имеет соответствующие значения зеленого цвета. Каждая сумма написана внизу. Результат суммирования слева направо дает окончательный ответ 2550. Следовательно, решение умножения 425 на 6 равно 2550.
Пример 2 - умножение на большее однозначное число
При умножении на более крупные одиночные цифры обычно при добавлении диагонального столбца сумма чисел дает число, равное 10 или больше.
Во втором примере вычисляется 6785 × 8.
Как и в примере 1, на доску помещаются кости, соответствующие наибольшему числу. В этом примере кости 6, 7, 8 и 5 были размещены в правильном порядке, как показано ниже.

В первом столбце находится число, на которое умножается наибольшее число. В этом примере номер был 8. Для оставшихся вычислений будет использоваться только строка 8, поэтому остальная часть доски очищена для ясности в объяснении оставшихся шагов.

Как и раньше, оценивается каждый диагональный столбец, начиная с правой стороны. Если сумма диагонального столбца равна 10 или больше, необходимо перенести разряд десятков этой суммы и добавить вместе с числами в соседнем левом столбце, как показано ниже.

После оценки каждого диагонального столбца вычисленные числа читаются слева направо для получения окончательного ответа; в этом примере было произведено 54280.
Следовательно: умножение 6785 на 8 дает 54280.
Пример 3 - умножение на многозначное число
В третьем примере вычисляется 825 × 913.
Кости, соответствующие ведущему числу, помещаются на доску. В этом примере кости 8, 2 и 5 были размещены в правильном порядке, как показано ниже.

Для умножения на многозначное число просматривается несколько строк. В этом примере строки для 9, 1 и 3 были удалены с доски для ясности.

Каждая строка оценивается индивидуально, и каждый диагональный столбец добавляется, как описано в предыдущих примерах. Суммы читаются слева направо, в результате чего получаются числа, необходимые для последующих вычислений сложения. В этом примере строка 9, строка 1 и строка 3 оценивались отдельно для получения результатов, показанных ниже.

Начиная с самой правой цифры второго числа, суммы помещаются из строк в последовательном порядке, если смотреть справа налево друг под другом, с использованием 0 в качестве заполнителя.
2475 8250 742500
Строки и заполнители суммируются для получения окончательного ответа.
2475 8250+ 742500 753225
В этом примере окончательный ответ был 753225. Следовательно: Решение умножения 825 на 913 - 753225.
Разделение
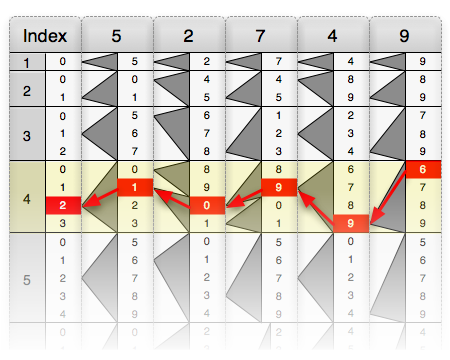
Деление выполняется аналогичным образом. Чтобы разделить 46785399 на 96431, полосы делителя (96431) помещаются на плату, как показано на рисунке ниже. Используя счеты, все произведения делителя от 1 до 9 находятся путем чтения отображаемых чисел. Обратите внимание, что дивиденд состоит из восьми цифр, тогда как частичные продукты (за исключением первого) имеют шесть цифр. Таким образом, две последние цифры числа 46785399, а именно "99", временно игнорируются, и остается число 467853. Затем определяется наибольшее частичное произведение, которое меньше усеченного делимого. В данном случае - 385724. Две вещи должны быть отмечены вниз, как видно на диаграмме: поскольку 385724 находится в строке «4» на счетах, цифра «4» отмечается вниз как крайняя левая цифра частного; частичный продукт, выровненный по левому краю, под исходным дивидендом также записывается. Два члена вычитаются, и остается 8212999. Те же шаги повторяются: число усекается до шести цифр, выбирается частичное произведение, непосредственно меньшее, чем усеченное число, номер строки записывается как следующая цифра частного, и частичное произведение вычитается из разницы, найденной в первом повторении. Процесс показан на схеме. Цикл повторяется до тех пор, пока результат вычитания не станет меньше делителя. Оставшееся число - это остаток.

Итак, в этом примере остается частное 485 с остатком 16364. Процесс обычно останавливается на этом, и в ответе используется дробная форма 485+16364/96431.
Для большей точности цикл продолжается, чтобы найти необходимое количество десятичных знаков. Десятичная точка помечается после последней цифры частного, а к остатку добавляется ноль, что оставляет 163640. Цикл продолжается, каждый раз добавляя ноль к результату после вычитания.
Извлечение квадратных корней
Для извлечения квадратного корня используется дополнительная кость, которая отличается от других тем, что имеет три столбца. В первом столбце находятся первые девять квадратных чисел, во втором - первые девять четных чисел, а в последнем - от 1 до 9.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | √ | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0⁄1 | 0⁄2 | 0⁄3 | 0⁄4 | 0⁄5 | 0⁄6 | 0⁄7 | 0⁄8 | 0⁄9 | 0⁄1 2 1 |
| 2 | 0⁄2 | 0⁄4 | 0⁄6 | 0⁄8 | 1⁄0 | 1⁄2 | 1⁄4 | 1⁄6 | 1⁄8 | 0⁄4 4 2 |
| 3 | 0⁄3 | 0⁄6 | 0⁄9 | 1⁄2 | 1⁄5 | 1⁄8 | 2⁄1 | 2⁄4 | 2⁄7 | 0⁄9 6 3 |
| 4 | 0⁄4 | 0⁄8 | 1⁄2 | 1⁄6 | 2⁄0 | 2⁄4 | 2⁄8 | 3⁄2 | 3⁄6 | 1⁄6 8 4 |
| 5 | 0⁄5 | 1⁄0 | 1⁄5 | 2⁄0 | 2⁄5 | 3⁄0 | 3⁄5 | 4⁄0 | 4⁄5 | 2⁄5 10 5 |
| 6 | 0⁄6 | 1⁄2 | 1⁄8 | 2⁄4 | 3⁄0 | 3⁄6 | 4⁄2 | 4⁄8 | 5⁄4 | 3⁄6 12 6 |
| 7 | 0⁄7 | 1⁄4 | 2⁄1 | 2⁄8 | 3⁄5 | 4⁄2 | 4⁄9 | 5⁄6 | 6⁄3 | 4⁄9 14 7 |
| 8 | 0⁄8 | 1⁄6 | 2⁄4 | 3⁄2 | 4⁄0 | 4⁄8 | 5⁄6 | 6⁄4 | 7⁄2 | 6⁄4 16 8 |
| 9 | 0⁄9 | 1⁄8 | 2⁄7 | 3⁄6 | 4⁄5 | 5⁄4 | 6⁄3 | 7⁄2 | 8⁄1 | 8⁄1 18 9 |
Чтобы найти квадратный корень из 46785399, его цифры сгруппированы в две, начиная справа, так что это выглядит так:
- 46785399
- Примечание: Число с нечетным числом цифр, например 85399, будет сгруппировано как 085399
Первой выбирается крайняя левая группа, в данном случае 46. Выбирается самый большой квадрат в квадратной корневой кости меньше 46, что составляет 36 из шестой строки. Первая цифра решения - 6, поскольку была выбрана шестая строка.
Затем на доске устанавливается число во втором столбце шестой строки квадратной корневой кости, 12.
Значение 36 в первом столбце шестой строки вычитается из 46, в результате остается 10.
Следующая группа цифр 78 добавляется рядом с 10; остается 1078.
На этом этапе плата и промежуточные расчеты должны выглядеть так:
| √46 78 53 99 = 6 − 36 10 78 |
Числа в каждой строке «считываются», игнорируя второй и третий столбцы из кости квадратного корня; они записаны. (Например, шестая строка читается как: 0⁄6 1⁄2 3⁄6 → 756).
Как и при умножении, показанном ранее, числа читаются справа налево и складываются диагональные числа сверху справа налево и снизу (6 + 0 = 6; 3 + 2 = 5; 1 + 6 = 7).
Найдено наибольшее число, меньшее текущего остатка, 1078 (из восьмой строки).
| √46 78 53 99 = 68 − 36 10 78 − 10 24 54 |
Как и раньше, добавляется 8, чтобы получить следующую цифру квадратного корня, а значение восьмой строки, 1024, вычитается из текущего остатка, 1078, чтобы получить 54. Второй столбец восьмой строки на квадратной корневой кости, 16, читается и номер выставляется на доске следующим образом.
Текущее число на доске - 12. Первая цифра 16 добавляется к 12, а вторая цифра 16 добавляется к результату. Итак, плата должна быть настроена на:
- 12 + 1 = 13 → добавить 6 → 136
- Примечание: Если во втором столбце кости квадратного корня есть только одна цифра, она добавляется к текущему числу на доске.
Доска и промежуточные расчеты теперь выглядят так.
| √46 78 53 99 = 68 − 36 10 78 − 10 24 54 53 |
И снова обнаруживается строка с наибольшим значением, меньшим, чем текущий частичный остаток, 5453. На этот раз это третья строка с 4089.
| √46 78 53 99 = 683 − 36 10 78 − 10 24 54 53 − 40 89 13 64 |
Следующая цифра квадратного корня - 3. Повторяются те же шаги, что и раньше, и 4089 вычитается из текущего остатка 5453, чтобы получить 1364 как следующий остаток. При перестановке доски во втором столбце квадратного корня кости будет 6, это одна цифра. Таким образом, 6 добавляется к текущему номеру на доске, 136, чтобы оставить 1366 на доске.
- 136 → добавить 6 → 1366
| √46 78 53 99 = 683 − 36 10 78 − 10 24 54 53 − 40 89 13 64 99 |
Процесс повторяется снова. Теперь наибольшее значение на доске, меньшее, чем текущий остаток, 136499, составляет 123021 от девятой строки.
Чтобы получить ответ, часто не нужно находить значение каждой строки. Строку, в которой есть ответ, можно угадать, посмотрев на число на нескольких первых костях и сравнив его с несколькими первыми цифрами остатка. Но диаграммы показывают значение всех строк, чтобы было понятно.
9 добавляется к результату, а 123021 вычитается из текущего остатка.
| √46 78 53 99 = 6839 − 36 10 78 − 10 24 54 53 − 40 89 13 64 99 − 12 30 21 1 34 78 |
Если все цифры были использованы, а остаток остался, то целая часть решена, но дробный бит все равно нужно найти.
Если целая часть решена, текущий результат возводится в квадрат (68392 = 46771921) должен быть наибольшим квадратом меньше 46785899.
Эта идея используется позже, чтобы понять, как работает методика, но может быть создано больше цифр.
Подобно нахождению дробной части в длинное деление, к остатку добавляются два нуля, чтобы получить новый остаток 1347800. Второй столбец девятой строки квадратной корневой кости равен 18, а текущее число на доске - 1366.
- 1366 + 1 → 1367 → добавить 8 → 13678
вычислено, чтобы установить на плате 13678.
Доска и промежуточные вычисления теперь выглядят следующим образом.
| √46 78 53 99.00 = 6839. − 36 10 78 − 10 24 54 53 − 40 89 13 64 99 − 12 30 21 1 34 78 00 |
Девятая строка с 1231101 является наибольшим значением, меньшим, чем оставшаяся, поэтому первая цифра дробной части квадратного корня равна 9.
| √46 78 53 99.00 = 6839.9 − 36 10 78 − 10 24 54 53 − 40 89 13 64 99 − 12 30 21 1 34 78 00 − 1 23 11 01 11 66 99 |
Значение девятой строки вычитается из остатка и добавляется еще несколько нулей, чтобы получить новый остаток 11669900. Во втором столбце девятой строки 18 с 13678 на доске, поэтому
- 13678 + 1 → 13679 → добавить 8 → 136798
вычислено, чтобы установить на плате 136798.
| √46 78 53 99.00 00 = 6839.9 − 36 10 78 − 10 24 54 53 − 40 89 13 64 99 − 12 30 21 1 34 78 00 − 1 23 11 01 11 66 99 00 |
Шаги можно продолжить, чтобы найти необходимое количество цифр и если будет достигнута необходимая точность. Если остаток равен нулю, это означает, что был найден точный квадратный корень.
Округления
Найдя нужное количество цифр, легко определить, нужно ли его округлять в большую сторону; т. е. изменение последней цифры. Не нужно искать другую цифру, чтобы увидеть, больше ли она 5. К корню добавляется 25 и сравнивается с остатком; если он меньше или равен остатку, то следующая цифра будет не менее пяти, и необходимо округление в большую сторону. В приведенном выше примере 6839925 меньше 11669900, поэтому корень необходимо округлить до 6840,0.
Чтобы найти квадратный корень из числа, которое не является целым числом, скажем 54782,917, все то же самое, за исключением того, что цифры слева и справа от десятичной точки сгруппированы по два.
Таким образом, 54782,917 можно сгруппировать как
- 054782.9170
Затем квадратный корень можно найти, используя ранее упомянутый процесс.
Диагональная модификация
В 19 веке кости Напьера были преобразованы, чтобы их было легче читать. Стержни были сделаны под углом около 65 °, так что треугольники, которые нужно было добавить, были выровнены вертикально. В этом случае в каждом квадрате стержня единица находится справа, а десятка (или ноль) - слева.

Стержни были сделаны таким образом, что вертикальные и горизонтальные линии были более заметными, чем линия, где стержни касались стержней, что облегчало чтение двух компонентов каждой цифры результата. Таким образом, на картинке сразу видно, что:
- 987654321 × 5 = 4938271605
Правители Genaille – Lucas
В 1891 г. Анри Женай изобрел вариант костей Напьера, который стал известен как Правители Genaille – Lucas. Представляя нести графически результаты простых задач умножения могут быть прочитаны напрямую, без промежуточных мысленных вычислений.
В следующем примере вычисляется 52749 × 4 = 210996.
| Вычислительные устройства в |
| Рабдология |
|---|
| Кости Напьера |
| Promptuary |
| Арифметика местоположения |
Смотрите также
Рекомендации
- ^ «Джон Нэпьер» (1617 г.). "Rabdologiæ" (на латыни). Эдинбург, Шотландия.
