Решетчатое умножение - Lattice multiplication
Решетчатое умножение, также известный как Итальянский метод, Китайский метод, Китайская решетка, размножение гелозии,[нужна цитата ] сито умножение, шабах, по диагонали или же Венецианские площади, это метод умножение который использует решетка для умножения двух многозначных чисел. Математически он идентичен более часто используемому длинное умножение алгоритм, но он разбивает процесс на более мелкие шаги, которые некоторым практикам легче использовать.[1]
Этот метод возник еще в средневековье и веками использовался во многих различных культурах. Его по-прежнему преподают в определенных учебных программах.[2][3]
Метод
Вычерчивается сетка, и каждая ячейка разбивается по диагонали. Два множимое вычисляемого продукта записываются вдоль верхней и правой стороны решетки, соответственно, по одной цифре на столбец сверху для первого множимого (число, записываемое слева направо), и по одной цифре в строке внизу справа для второго множимого (число пишется сверху вниз). Затем каждая ячейка решетки заполняется произведением ее цифры столбца и строки.
В качестве примера рассмотрим умножение 58 на 213. После записи множителей по бокам рассмотрите каждую ячейку, начиная с верхней левой ячейки. В этом случае цифра столбца - 5, а цифра строки - 2. Запишите их произведение, 10, в ячейку, указав цифру 1 над диагональю и цифру 0 под диагональю (см. Рисунок для шага 1).
Если в простом продукте отсутствует цифра в разряде десятков, просто введите 0 в разряде десятков.[1]
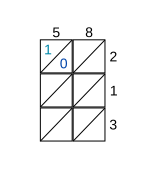
После того, как все ячейки будут заполнены таким образом, цифры на каждой диагонали суммируются, начиная от нижней правой диагонали к верхней левой. Каждая диагональная сумма записывается там, где заканчивается диагональ. Если сумма содержит более одной цифры, значение разряда десятков переносится на следующую диагональ (см. Шаг 2).
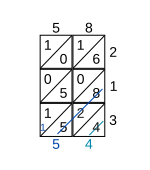
Цифры заполняются слева и снизу сетки, и ответ - числа, считанные снизу (слева) и поперек (снизу). В показанном примере результат умножения 58 на 213 составляет 12354.
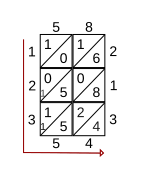
Умножение десятичных дробей
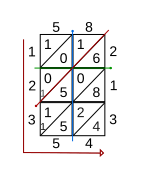
Решетчатую технику можно также использовать для умножения десятичные дроби. Например, умножение 5,8 на 2,13 происходит так же, как умножение 58 на 213, как описано в предыдущем разделе. Чтобы найти положение десятичной точки в окончательном ответе, можно провести вертикальную линию от десятичной точки в 5.8 и горизонтальную линию от десятичной точки в 2.13. (См. Рисунок к шагу 4.) Диагональ сетки через пересечение этих двух линий определяет положение десятичной точки в результате.[1] В показанном примере результат умножения 5,8 и 2,13 равен 12,354.
История
Умножение решетки исторически использовалось во многих различных культурах. Неизвестно, где он возник вначале и развивался ли он независимо более чем в одном регионе мира.[4] Самое раннее зарегистрированное использование решеточного умножения:[5]
- в арабской математике был Ибн аль-Банна аль-Марракуши в его Талхих аль-Шисаб, в Магрибе в конце 13 века
- в европейской математике неизвестный автор латинского трактата в Англии, Tractatus de minutisphilusphicis et vulgaribus, c. 1300
- в китайской математике был У Цзин в его Цзючжан суанфа билей дацюань, завершена в 1450 году.
Математик и педагог Дэвид Юджин Смит утверждал, что решеточное умножение было принесено в Италию с Ближнего Востока.[6] Это подтверждается тем, что арабский термин, обозначающий метод, шабах, имеет то же значение, что и итальянский термин, обозначающий метод, гелозия, а именно металлическую решетку или решетку (решетку) для окна.
Иногда ошибочно утверждается, что решеточное умножение описывалось формулой Мухаммад ибн Муса аль-Хваризми (Багдад, ок. 825 г.) или Фибоначчи в его Liber Abaci (Италия, 1202, 1228).[7] На самом деле, однако, ни один из этих двух авторов не нашел использования решеточного умножения. В главе 3 его Liber Abaci, Фибоначчи описывает родственную технику умножения тем, что он назвал quadrilatero in forma scacherii («Прямоугольник в виде шахматной доски»). В этой технике квадратные клетки не делятся по диагонали; в каждую ячейку записывается только цифра младшего разряда, в то время как любая цифра более высокого порядка должна быть запомнена или записана в другом месте, а затем «перенесена» для добавления в следующую ячейку. Это отличается от решеточного умножения, отличительной чертой которого является то, что каждая ячейка прямоугольника имеет собственное правильное место для цифры переноса; это также означает, что ячейки можно заполнять в любом желаемом порядке. Swetz[8] сравнивает и противопоставляет умножение на гелозия (решетка), по scacherii (шахматная доска) и другие табличные методы.
Другие известные исторические применения решеточного умножения включают:[5]
- Джамшид аль-Каши С Мифтах аль-Шисаб (Самарканд, 1427), в котором используются шестидесятеричные числа (основание 60), а сетка повернута на 45 градусов в сторону «ромба».
- в Arte dell’Abbaco, анонимный текст, опубликованный на венецианском диалекте в 1478 году, часто называемый Тревизо Арифметика потому что он был напечатан в Тревизо, недалеко от Венеции, Италия
- Лука Пачоли С Summa de arithmetica (Венеция, 1494 г.)
- комментарий индийского астронома Ганеши к Бхаскара II С Лилавати (16-ый век).
Производные
Выводы этого метода также появились в трудах 16 века. Умдет-уль-Хисаб к Османско-Боснийский эрудит Матракчи Насух.[9] Матракчи Насух Треугольная версия метода умножения показана в примере, показывающем 155 x 525 справа, и объяснена в примере, показывающем 236 x 175 на левом рисунке.[10]

Тот же принцип, описанный Матракчи Насух лежали в основе более позднего развития счетных стержней, известных как Кости Напьера (Шотландия, 1617 г.) и Правители Genaille – Lucas (Франция, конец 1800-х гг.).
Рекомендации
- ^ а б c Томас, Вики (2005). "Решеточное умножение". Изучите NC. Школа образования UNC. Получено 4 июля 2014.
- ^ Боаг, Элизабет, "Умножение на решетке", Бюллетень BSHM: Журнал Британского общества истории математики 22: 3 (ноябрь 2007 г.), с. 182.
- ^ Наджент, Патрисия М., «Умножение решетки в классе Preservice», Преподавание математики в средней школе 13: 2 (сентябрь 2007 г.), стр. 110–113.
- ^ Жан-Люк Шабер, изд., История алгоритмов: от гальки до микрочипа (Берлин: Springer, 1999), стр. 21.
- ^ а б Жан-Люк Шабер, изд., История алгоритмов: от гальки до микрочипа (Берлин: Springer, 1999), стр. 21-26.
- ^ Смит, Дэвид Юджин, История математики, Vol. 2, «Специальные разделы элементарной математики» (Нью-Йорк: Довер, 1968).
- ^ Оригинальная версия 1202 г. Liber Abaci потерян. Версия 1228 года была позже опубликована на оригинальной латыни в Boncompagni, Baldassarre, Скритти ди Леонардо Пизано, т. 1 (Рим: Типография делле научная математика и физика, 1857 г.); английский перевод того же был опубликован Sigler, Laurence E., Liber Abaci Фибоначчи: перевод на современный английский язык расчетов Леонардо Пизано (Нью-Йорк: Springer Verlag, 2002).
- ^ Свец, Фрэнк Дж., Капитализм и арифметика: новая математика XV века, включая полный текст арифметики Тревизо 1478 года, переведенный Дэвидом Юджином Смитом (La Salle, IL: Open Court, 1987), стр. 205-209.
- ^ Корлу, М.С., Берлбо, Л.М., Капраро, Р.М., Корлу, М.А., и Хан, С. (2010). «Школа Османского дворца Эндерун и Человек с множеством талантов, Матракчи Насух». Журнал Корейского общества математического образования, Серия D: Исследования в области математического образования. 14 (1), стр. 19-31.
- ^ https://tamu.academia.edu/SencerCorlu/Papers/471488/The_Ottoman_Palace_School_Enderun_and_the_Man_with_Multiple_Talents_Matrakci_Nasuh
