Обратная кинематика - Inverse kinematics

Прямая и обратная кинематика

В компьютерная анимация и робототехника, обратная кинематика представляет собой математический процесс расчета переменных параметров соединения, необходимых для размещения конца кинематическая цепь, например, робот-манипулятор или скелет анимационного персонажа, в заданном положении и ориентации относительно начала цепочки. При заданных параметрах соединения положение и ориентация конца цепи, например рука персонажа или робота, как правило, может быть вычислена напрямую с использованием нескольких приложений тригонометрических формул, процесс, известный как передняя кинематика. Однако обратная операция, как правило, намного сложнее.^[1]

Обратная кинематика также используется для восстановления движений объекта в мире из некоторых других данных, таких как фильм этих движений или фильм мира, видимого камерой, которая сама совершает эти движения. Это происходит, например, когда должны быть сняты движения актера-человека. продублирован анимированным персонажем.

Робототехника

В робототехнике обратная кинематика использует кинематика уравнения для определения совместных параметров, которые обеспечивают желаемую конфигурацию (положение и вращение) для каждого из конечные эффекторы.^[2] Определение движения робота таким образом, чтобы его рабочие органы переходили из начальной конфигурации в желаемую, известно как планирование движения. Обратная кинематика превращает план движения в сустав привод траектории для робота. Подобные формулы определяют положение скелета анимированный персонаж то есть движение определенным образом в фильме или в транспортном средстве, таком как автомобиль или лодка, содержащем камеру, которая снимает сцену из фильма. Как только движения транспортного средства известны, их можно использовать для определения постоянно меняющейся точки обзора для компьютерных изображений объектов ландшафта, таких как здания, чтобы эти объекты изменялись в перспектива в то время как они, кажется, не двигаются, когда камера проезжает мимо них.

Движение кинематическая цепь, будь то робот или анимированный персонаж, моделируется уравнениями кинематики цепи. Эти уравнения определяют конфигурацию цепи с точки зрения ее совместных параметров. Прямая кинематика использует параметры соединения для вычисления конфигурации цепи, а обратная кинематика обращает это вычисление, чтобы определить параметры соединения, которые достигают желаемой конфигурации.^[3]^[4]^[5]

Кинематический анализ

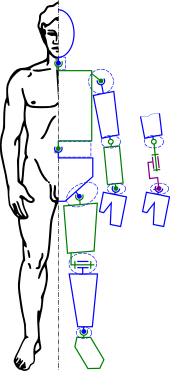
Модель скелета человека в виде кинематической цепи позволяет позиционировать его с помощью обратной кинематики.

Кинематический анализ - один из первых шагов в проектировании большинства промышленных роботов. Кинематический анализ позволяет проектировщику получать информацию о положении каждого компонента в механической системе. Эта информация необходима для последующего динамического анализа вместе с путями управления.

Обратная кинематика - это пример кинематического анализа системы твердых тел со связями, или кинематическая цепь. В кинематические уравнения робота можно использовать для определения петлевых уравнений сложной шарнирной системы. Эти петлевые уравнения являются нелинейными ограничениями на параметры конфигурации системы. Независимые параметры в этих уравнениях известны как степени свободы системы.

Хотя аналитические решения проблемы обратной кинематики существуют для широкого диапазона кинематических цепей, инструменты компьютерного моделирования и анимации часто используют Метод Ньютона для решения уравнений нелинейной кинематики.

Другие применения алгоритмов обратной кинематики включают: интерактивное манипулирование, управление анимацией и избежание столкновения.

Обратная кинематика и 3D-анимация

Обратная кинематика важна для программирование игр и 3D анимация, где он используется для подключения игровые персонажи физически по отношению к миру, например, ноги твердо приземляются на поверхность (см. ^[6] для комплексного исследования Методы обратной кинематики, используемые в компьютерной графике ).

Анимированная фигура моделируется каркасом из жестких сегментов, соединенных суставами, который называется кинематическая цепь. Уравнения кинематики фигуры определяют соотношение между углами сочленения фигуры и ее позой или конфигурацией. В прямая кинематическая анимация Задача использует уравнения кинематики для определения позы с учетом углов суставов. В обратная кинематическая задача вычисляет суставные углы для желаемой позы фигуры.

Компьютерным дизайнерам, художникам и аниматорам часто проще определить пространственную конфигурацию сборки или фигуры с помощью движущихся частей или рук и ног, чем напрямую манипулировать углами суставов. Следовательно, обратная кинематика используется в системах автоматизированного проектирования для анимации сборок, а компьютерные художники и аниматоры - для позиционирования фигур и персонажей.

Сборка моделируется как жесткие связи, соединенные соединениями, которые определены как сопряжения или геометрические ограничения. Движение одного элемента требует вычисления углов сочленения других элементов для сохранения совместные ограничения. Например, обратная кинематика позволяет художнику перемещать руку трехмерной модели человека в желаемое положение и ориентацию и иметь алгоритм, выбирающий правильные углы суставов запястья, локтя и плеча. Успешная реализация компьютера анимация обычно также требует, чтобы фигура двигалась в разумных пределах. антропоморфный пределы.

Метод сравнения прямой и обратной кинематики для анимации персонажа можно определить по преимуществам, присущим каждому из них. Например, блокирующая анимация, в которой используются большие дуги движения, часто более выгодна в прямой кинематике. Однако более тонкая анимация и позиционирование целевого рабочего органа по отношению к другим моделям может быть проще при использовании инвертированной кинематики. Современные пакеты цифрового создания (DCC) предлагают методы для применения к моделям как прямой, так и обратной кинематики.

Аналитические решения обратной кинематики

В некоторых случаях, но не во всех, существуют аналитические решения обратных кинематических задач. Одним из таких примеров является робот с 6 степенями свободы (например, 6 поворотных шарниров), движущийся в трехмерном пространстве (с 3 степенями свободы положения и 3 степенями свободы вращения). Если степени свободы робота превышают степени свободы рабочего органа, например, у робота с 7 степенями свободы и 7 поворотными шарнирами, то существует бесконечно много решений проблемы IK, и аналитического решения не существует. Дальнейшее расширение этого примера позволяет исправить одно соединение и аналитически решить для других соединений, но, возможно, лучшее решение предлагают численные методы (следующий раздел), которые вместо этого могут оптимизировать решение с учетом дополнительных предпочтений (затраты в задаче оптимизации ).

Аналитическое решение обратной кинематической задачи - это выражение в замкнутой форме, которое принимает позу рабочего органа в качестве входных данных и дает положения суставов в качестве выходных данных, ${ Displaystyle д = е (х)}$ . Аналитические решатели обратной кинематики могут быть значительно быстрее, чем численные решатели, и предоставлять более одного решения, но только конечное число решений для данной позы рабочего органа.

В IKFast Программа с открытым исходным кодом может найти полные аналитические решения для наиболее распространенных роботов-манипуляторов и сгенерировать для них код на C ++. Сгенерированные решатели охватывают большинство вырожденных случаев и могут завершиться за микросекунды на современных компьютерах.^{[рекламный язык ]}. Одна проблема с этими решателями заключается в том, что они, как известно, не обязательно дают локально гладкие решения между двумя соседними конфигурациями, что может вызвать нестабильность, если требуются итерационные решения обратной кинематики, например, если IK решается внутри высокоскоростного контура управления. .

Численные решения задач ИК

Существует множество методов моделирования и решения обратных задач кинематики. Наиболее гибкие из этих методов обычно полагаются на итеративная оптимизация найти приближенное решение из-за сложности обращения уравнения прямой кинематики и возможности пустого пространство решений. Основная идея, лежащая в основе некоторых из этих методов, состоит в моделировании уравнения прямой кинематики с использованием Серия Тейлор расширение, которое может быть проще инвертировать и решить, чем исходную систему.

Обратный метод Якоби

В Якобиан Обратный метод - это простой, но эффективный способ реализации обратной кинематики. Пусть будет ${ displaystyle m}$ переменные, которые управляют уравнением прямой кинематики, то есть функцией положения. Эти переменные могут быть углами сочленения, длиной или другими произвольными действительными значениями. Если система IK живет в трехмерном пространстве, функцию положения можно рассматривать как отображение ${ Displaystyle р (х): Re ^ {m} rightarrow Re ^ {3}}$ . Позволять ${ displaystyle p_ {0} = p (x_ {0})}$ дать начальное положение системы, и

{ displaystyle p_ {1} = p (x_ {0} + Delta x)}

быть целевой позицией системы. Обратный метод Якоби итеративно вычисляет оценку ${ displaystyle Delta x}$ что минимизирует ошибку, задаваемую ${ displaystyle || p (x_ {0} + Delta x_ {оценка}) - p_ {1} ||}$ .

Для малых ${ displaystyle Delta x}$ -векторы, разложение функции положения в ряд дает

{ displaystyle p (x_ {1}) приблизительно p (x_ {0}) + J_ {p} (x_ {0}) Delta x}

,

куда ${ displaystyle J_ {p} (x_ {0})}$ это (3 × m) Матрица якобиана функции положения при ${ displaystyle x_ {0}}$ .

Обратите внимание, что (i, k) -й элемент матрицы Якоби можно аппроксимировать численно

{ displaystyle { frac { partial p_ {i}} { partial x_ {k}}} приблизительно { frac {p_ {i} (x_ {0, k} + h) -p_ {i} (x_ {0})} {h}}}

,

куда ${ Displaystyle p_ {я} (х)}$ дает i-й компонент функции позиции, ${ displaystyle x_ {0, k} + h}$ просто ${ displaystyle x_ {0}}$ с небольшой дельтой, добавленной к его k-му компоненту, и ${ displaystyle h}$ - относительно небольшое положительное значение.

Принимая Псевдообратная матрица Мура-Пенроуза якобиана (вычисляемого с помощью разложение по сингулярным числам ) и изменение условий приводит к

{ displaystyle Delta x приблизительно J_ {p} ^ {+} (x_ {0}) Delta p}

,

куда ${ Displaystyle Delta p = p (x_ {0} + Delta x) -p (x_ {0})}$ .

Применение метода обратного якобиана один раз приведет к очень грубой оценке желаемого ${ displaystyle Delta x}$ -вектор. А линейный поиск следует использовать для масштабирования этого ${ displaystyle Delta x}$ до приемлемого значения. Оценка на ${ displaystyle Delta x}$ можно улучшить с помощью следующего алгоритма (известного как Ньютон-Рафсон метод):

{ displaystyle Delta x_ {k + 1} = J_ {p} ^ {+} (x_ {k}) Delta p_ {k}}

Когда-то некоторые ${ displaystyle Delta x}$ -vector привел к тому, что ошибка упала почти до нуля, алгоритм должен завершиться. Существующие методы, основанные на Матрица Гессе системы, как сообщается, сходятся к желаемому ${ displaystyle Delta x}$ значения, используя меньшее количество итераций, хотя в некоторых случаях больше вычислительных ресурсов.

Эвристические методы

Проблема обратной кинематики также может быть аппроксимирована эвристическими методами. Эти методы выполняют простые итерационные операции, постепенно приводящие к приближению решения. Эвристические алгоритмы имеют низкую вычислительную стоимость (очень быстро возвращают окончательную позу) и обычно поддерживают совместные ограничения. Наиболее популярные эвристические алгоритмы: Циклический координатный спуск (CCD),^[7] и Прямая и обратная обратная кинематика (ФАБРИК).^[8]

Смотрите также

внешняя ссылка

Прямая и обратная обратная кинематика (FABRIK)
Робототехника и 3D-анимация в FreeBasic (на испанском)
Аналитический решатель обратной кинематики - Учитывая описание кинематики робота OpenRAVE, генерирует файл C ++, который аналитически решает для полного IK.
Алгоритмы обратной кинематики
Робот Обратное решение для общей геометрии робота
Статья HowStuffWorks.com Как персонажи видеоигр двигаются так плавно? с объяснением обратной кинематики
3D-анимация расчета геометрической обратной кинематики промышленного робота
Кинематика 3D Теории
Белковая обратная кинематика
Пример простой обратной кинематики с исходным кодом с использованием якобиана
Подробное описание якобианов и решений ПЗС для обратной кинематики
Autodesk HumanIK
3D визуализация аналитического решения промышленного робота

[1] Дональд Л. Пайпер, Кинематика манипуляторов под управлением компьютера. Кандидатская диссертация, Стэнфордский университет, факультет машиностроения, 24 октября 1968 г.

[2] Пол, Ричард (1981). Роботы-манипуляторы: математика, программирование и управление: компьютерное управление роботами-манипуляторами. MIT Press, Кембридж, Массачусетс. ISBN 978-0-262-16082-7.

[3] Дж. М. Маккарти, 1990 г., Введение в теоретическую кинематику, MIT Press, Кембридж, Массачусетс.

[Uicker2003-4] Дж. Дж. Уикер, Г. Р. Пеннок и Дж. Э. Шигли, 2003 г., Теория машин и механизмов, Издательство Оксфордского университета, Нью-Йорк.

[McCarthy2010-5] Дж. М. Маккарти и Г. С. Со, 2010 г., Геометрический дизайн связей, Спрингер, Нью-Йорк.

[6] А. Аристиду, Дж. Ласенби, Я. Хрисанту, А. Шамир. Методы обратной кинематики в компьютерной графике: обзор. Форум компьютерной графики, 37 (6): 35-58, 2018.

[7] Д. Г. Люенбергер. 1989. Линейное и нелинейное программирование. Эддисон Уэсли.

[8] А. Аристиду и Дж. Ласенби. 2011 г. FABRIK: быстрое итерационное решение обратной кинематической задачи.. График. Модели 73, 5, 243–260.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]