Бесконечная диэдральная группа - Infinite dihedral group
Эта статья нужны дополнительные цитаты для проверка. (Июль 2011 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
| p1m1, (*∞∞ ) | р2, (22∞) | p2mg, (2 * ∞) |
|---|---|---|
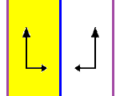 |  |  |
| В 2-х мерном трех фризовые группы p1m1, p2 и p2mg изоморфны Dih∞ группа. У всех есть 2 генератора. Первая имеет две параллельные линии отражения, вторая - два двукратных вращения, а последняя - одно зеркало и одно двукратное вращение. | ||
В математика, то бесконечная диэдральная группа Dih∞ является бесконечная группа со свойствами, аналогичными свойствам конечного диэдральные группы.
В двумерная геометрия, то бесконечная диэдральная группа представляет группа фризов симметрия p1m1, рассматриваемый как бесконечный набор параллельных отражений вдоль оси.
Определение
Каждая группа диэдра порождается вращением р и отражение; если вращение является рациональным кратным полного вращения, то существует некоторое целое число п такой, что рп - единица, и мы имеем конечную группу диэдра порядка 2п. Если вращение нет рациональное кратное полному обороту, то такого п и получившаяся группа бесконечно много элементов и называется Dih∞. Она имеет презентации
и изоморфен полупрямой продукт из Z и Z/ 2, и бесплатный продукт Z/2 * Z/ 2. Это группа автоморфизмов графа, состоящего из пути, бесконечного в обе стороны. Соответственно, это группа изометрии из Z (смотрите также группы симметрии в одном измерении ) группа перестановок α: Z → Z удовлетворение |я - j| = | α (я) - α (j) |, для всех я, j в Z.[2]
Бесконечную группу диэдра также можно определить как голоморф из бесконечная циклическая группа.
Сглаживание

Пример бесконечной двугранной симметрии в сглаживание сигналов с действительным знаком.
При выборке функции на частоте жs (интервалы 1/жs) следующие функции дают идентичные наборы выборок: {sin (2π ( f + Nfs) т + φ), N = 0, ±1, ±2, ±3,...}. Таким образом, обнаруженное значение частоты ж является периодический, что дает элемент перевода р = жs. Функции и их частоты называются псевдонимы друг друга. Отмечая тригонометрическую идентичность:
мы можем записать все частоты псевдонимов как положительные значения:| ж+N fs|. Это дает отражение (ж) элемент, а именно ж ↦ −ж. Например, с ж = 0.6жs иN = −1, f + Nfs = −0.4жs отражает к0.4жs, что дает две крайние левые черные точки на рисунке.[примечание 1] Две другие точки соответствуют N = −2 иN = 1. Как показано на рисунке, имеются симметрии отражения на 0,5жs, жs, 1.5жsи т. д. Формально частное при наложении имен орбифолд [0, 0.5жs], с Z/ 2 действие в конечных точках (точках орбифолда), соответствующее отражению.
Смотрите также
- В ортогональная группа O (2), еще одно бесконечное обобщение конечных групп диэдра
Примечания
- ^ В обработка сигналов симметрия относительно оси жs/2 известен как складывание, и ось известна как частота складывания.
Рекомендации
- ^ Коннолли, Фрэнсис; Дэвис, Джеймс (август 2004 г.). «Группы препятствий к перестройкам бесконечной диэдральной группы». Геометрия и топология. 8 (3): 1043–1078. arXiv:математика / 0306054. Дои:10.2140 / gt.2004.8.1043.
- ^ Минакси Бхаттачарджи, Дугальд Макферсон, Рёгнвальдур Г. Мёллер, Питер М. Нойман. Заметки о бесконечных группах перестановок, выпуск 1689. Springer, 1998. п. 38. ISBN 978-3-540-64965-6



