Теория пластичности течения - Flow plasticity theory

Пластическая деформация тонкого металлического листа.

Пластичность потока это механика твердого тела теория, которая используется для описания пластик поведение материалов.^[1] Теории пластичности течения характеризуются предположением, что правило потока существует, который можно использовать для определения степени пластической деформации материала.

В теориях пластичности течения предполагается, что общая напряжение в теле можно аддитивно (или мультипликативно) разложить на упругую часть и пластическую часть. Упругая часть деформации может быть вычислена из линейная эластичность или же сверхупругий конститутивная модель. Однако для определения пластической части деформации требуется правило потока и модель упрочнения.

Теория малых деформаций

Кривая "напряжение-деформация", показывающая типичное пластическое поведение материалов при одноосном сжатии. Деформация может быть разложена на восстанавливаемую упругую деформацию (${\displaystyle \varepsilon _{e}}$) и неупругой деформации (${\displaystyle \varepsilon _{p}}$). Напряжение при начальной текучести составляет ${\displaystyle \sigma _{0}}$. Для материалов с деформационным упрочнением (как показано на рисунке) предел текучести увеличивается с увеличением пластической деформации до значения ${\displaystyle \sigma _{y}}$.

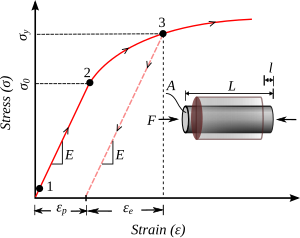
Типичные теории пластичности потока для однонаправленного нагружения (идеальная пластичность при малых деформациях или пластичность при упрочнении) разрабатываются на основе следующих требований:

1. Материал имеет линейный диапазон упругости.
2. Материал имеет предел упругости, определяемый как напряжение, при котором сначала происходит пластическая деформация, т. Е. ${\displaystyle \sigma =\sigma _{0}}$.
3. За пределами упругости напряженное состояние всегда остается на поверхности текучести, т. Е. ${\displaystyle \sigma =\sigma _{y}}$.
4. Нагрузка определяется как ситуация, при которой приращение напряжения больше нуля, т. Е. ${\displaystyle d\sigma >0}$. Если нагружение переводит напряженное состояние в пластическую область, то приращение пластической деформации всегда больше нуля, т.е. ${\displaystyle d\varepsilon _{p}>0}$.
5. Разгрузка определяется как ситуация, при которой приращения напряжения меньше нуля, т. Е. ${\displaystyle d\sigma <0}$. Материал эластичен при разгрузке и не накапливает дополнительную пластическую деформацию.
6. Полная деформация представляет собой линейную комбинацию упругой и пластической частей, т. Е. ${\displaystyle d\varepsilon =d\varepsilon _{e}+d\varepsilon _{p}}$. Пластиковая часть не может быть восстановлена, в то время как эластичная часть полностью восстанавливается.
7. Работа, выполненная в цикле загрузки-разгрузки, положительна или равна нулю, т. Е. ${\displaystyle d\sigma \,d\varepsilon =d\sigma \,(d\varepsilon _{e}+d\varepsilon _{p})\geq 0}$. Это также называется Стабильность Друкера постулирует и исключает возможность смягчения деформации.

Вышеупомянутые требования могут быть выражены в трехмерных состояниях напряжения и разнонаправленной нагрузки следующим образом.

• Эластичность (Закон Гука ). В линейно-упругом режиме напряжения и деформации в материале связаны соотношением

${\displaystyle {\boldsymbol {\sigma }}={\mathsf {D}}:{\boldsymbol {\varepsilon }}}$

где матрица жесткости ${\displaystyle {\mathsf {D}}}$ постоянно.

• Предел упругости (Поверхность выхода ). Предел упругости определяется поверхностью текучести, которая не зависит от пластической деформации и имеет вид

${\displaystyle f({\boldsymbol {\sigma }})=0\,.}$

• За пределом упругости. Для материалов с деформационным упрочнением поверхность текучести развивается с увеличением пластической деформации и изменяется предел упругости. Эволюционирующая поверхность текучести имеет вид

${\displaystyle f({\boldsymbol {\sigma }},{\boldsymbol {\varepsilon }}_{p})=0\,.}$

• Загрузка. Для общих напряженных состояний пластик загрузка отображается, если состояние напряжения находится на поверхности текучести, а приращение напряжения направлено наружу от поверхности текучести; это происходит, если внутреннее произведение приращения напряжения и внешней нормали поверхности текучести положительно, т. е.

${\displaystyle d{\boldsymbol {\sigma }}:{\frac {\partial f}{\partial {\boldsymbol {\sigma }}}}\geq 0\,.}$

Приведенное выше уравнение, когда оно равно нулю, указывает на состояние нейтральная загрузка где напряженное состояние движется по поверхности текучести.

• Разгрузка: Аналогичный аргумент приводится для разгрузки в какой ситуации ${\displaystyle f<0}$, материал находится в упругой области, и

${\displaystyle d{\boldsymbol {\sigma }}:{\frac {\partial f}{\partial {\boldsymbol {\sigma }}}}<0\,.}$

• Разложение штамма: Аддитивное разложение деформации на упругую и пластическую части можно записать как

${\displaystyle d{\boldsymbol {\varepsilon }}=d{\boldsymbol {\varepsilon }}_{e}+d{\boldsymbol {\varepsilon }}_{p}\,.}$

• Постулат стабильности: Постулат стабильности выражается как

${\displaystyle d{\boldsymbol {\sigma }}:d{\boldsymbol {\varepsilon }}\geq 0\,.}$

Правило потока

В случае пластичности металлов предположение о том, что приращение пластической деформации и тензор девиаторных напряжений имеют одинаковые основные направления, заключено в соотношение, называемое соотношением правило потока. Теории пластичности горных пород также используют аналогичную концепцию, за исключением того, что требование зависимости поверхности текучести от давления требует ослабления вышеуказанного предположения. Вместо этого обычно предполагается, что приращение пластической деформации и нормаль к поверхности текучести, зависящей от давления, имеют одинаковое направление, т. Е.

${\displaystyle d{\boldsymbol {\varepsilon }}_{p}=d\lambda \,{\frac {\partial f}{\partial {\boldsymbol {\sigma }}}}}$

куда ${\displaystyle d\lambda >0}$ параметр упрочнения. Эта форма правила потока называется связанное правило потока а предположение о сонаправленности называется условие нормальности. Функция ${\displaystyle f}$ также называется пластический потенциал.

Вышеуказанное правило потока легко оправдывается для идеально пластических деформаций, для которых ${\displaystyle d{\boldsymbol {\sigma }}=0}$ когда ${\displaystyle d{\boldsymbol {\varepsilon }}_{p}>0}$, т.е. поверхность текучести остается постоянной при увеличении пластической деформации. Это означает, что приращение упругой деформации также равно нулю, ${\displaystyle d{\boldsymbol {\varepsilon }}_{e}=0}$, по закону Гука. Следовательно,

${\displaystyle d{\boldsymbol {\sigma }}:{\frac {\partial f}{\partial {\boldsymbol {\sigma }}}}=0\quad {\text{and}}\quad d{\boldsymbol {\sigma }}:d{\boldsymbol {\varepsilon }}_{p}=0\,.}$

Следовательно, и нормаль к поверхности текучести, и тензор пластической деформации перпендикулярны тензору напряжений и должны иметь одинаковое направление.

Для упрочнение материала поверхность текучести может расширяться с увеличением напряжения. Мы принимаем второй постулат устойчивости Друкера, который гласит, что для бесконечно малого цикла напряжений эта пластическая работа положительна, т. Е.

${\displaystyle d{\boldsymbol {\sigma }}:d{\boldsymbol {\varepsilon }}_{p}\geq 0\,.}$

Для чисто упругих циклов указанная величина равна нулю. Изучение работы, выполненной в течение цикла загрузки-разгрузки пластика, может быть использовано для обоснования применимости соответствующего правила потока.^[2]

Условие согласованности

В Условие согласованности Прагера необходимо для замыкания системы определяющих уравнений и исключения неизвестного параметра ${\displaystyle d\lambda }$ из системы уравнений. Условие согласованности гласит, что ${\displaystyle df=0}$ на выходе, потому что ${\displaystyle f({\boldsymbol {\sigma }},{\boldsymbol {\varepsilon }}_{p})=0}$, и поэтому

${\displaystyle df={\frac {\partial f}{\partial {\boldsymbol {\sigma }}}}:d{\boldsymbol {\sigma }}+{\frac {\partial f}{\partial {\boldsymbol {\varepsilon }}_{p}}}:d{\boldsymbol {\varepsilon }}_{p}=0\,.}$

Теория больших деформаций

Теории пластичности при больших деформациях обычно начинаются с одного из следующих предположений:

• в скорость деформации тензор можно аддитивно разложить на упругую часть и пластическую часть, или
• в градиент деформации тензор можно мультипликативно разложить на упругую и пластическую части.

Первое предположение широко использовалось для численного моделирования металлов, но постепенно было вытеснено мультипликативной теорией.

Кинематика мультипликативной пластичности

Концепция мультипликативного разложения градиента деформации на упругую и пластическую части была впервые независимо предложена Б. А. Билби,^[3] Э. Крёнер,^[4] в контексте кристаллическая пластичность и расширен до континуальной пластичности Эразмом Ли.^[5] В разложении предполагается, что полный градиент деформации (F) можно разложить как:

${\displaystyle {\boldsymbol {F}}={\boldsymbol {F}}^{e}\cdot {\boldsymbol {F}}^{p}}$

куда F^е - упругая (восстанавливаемая) часть и F^п пластическая (невосстановимая) часть деформации. В градиент пространственной скорости дан кем-то

${\displaystyle {\begin{aligned}{\boldsymbol {l}}&={\dot {\boldsymbol {F}}}\cdot {\boldsymbol {F}}^{-1}=\left({\dot {\boldsymbol {F}}}^{e}\cdot {\boldsymbol {F}}^{p}+{\boldsymbol {F}}^{e}\cdot {\dot {\boldsymbol {F}}}^{p}\right)\cdot \left[({\boldsymbol {F}}^{p})^{-1}\cdot ({\boldsymbol {F}}^{e})^{-1}\right]\\&={\dot {\boldsymbol {F}}}^{e}\cdot ({\boldsymbol {F}}^{e})^{-1}+{\boldsymbol {F}}^{e}\cdot [{\dot {\boldsymbol {F}}}^{p}\cdot ({\boldsymbol {F}}^{p})^{-1}]\cdot ({\boldsymbol {F}}^{e})^{-1}\,.\end{aligned}}}$

где наложенная точка указывает производную по времени. Мы можем записать это как

${\displaystyle {\boldsymbol {l}}={\boldsymbol {l}}^{e}+{\boldsymbol {F}}^{e}\cdot {\boldsymbol {L}}^{p}\cdot ({\boldsymbol {F}}^{e})^{-1}\,.}$

Количество

${\displaystyle {\boldsymbol {L}}^{p}:={\dot {\boldsymbol {F}}}^{p}\cdot ({\boldsymbol {F}}^{p})^{-1}}$

называется пластический градиент скорости и определяется в промежуточном (несовместимый ) конфигурация без напряжений. Симметричная часть (D^п) из L^п называется пластическая скорость деформации а кососимметричная часть (W^п) называется пластиковый спин:

${\displaystyle {\boldsymbol {D}}^{p}={\tfrac {1}{2}}[{\boldsymbol {L}}^{p}+({\boldsymbol {L}}^{p})^{T}]~,~~{\boldsymbol {W}}^{p}={\tfrac {1}{2}}[{\boldsymbol {L}}^{p}-({\boldsymbol {L}}^{p})^{T}]\,.}$

Обычно пластический спин игнорируется в большинстве описаний конечной пластичности.

Упругий режим

Упругое поведение в режиме конечной деформации обычно описывается сверхупругий материал модель. Упругую деформацию можно измерить с помощью эластичного правого Тензор деформации Коши-Грина определяется как:

${\displaystyle {\boldsymbol {C}}^{e}:=({\boldsymbol {F}}^{e})^{T}\cdot {\boldsymbol {F}}^{e}\,.}$

В логарифмический или же Генки штамм тензор может быть определен как

${\displaystyle {\boldsymbol {E}}^{e}:={\tfrac {1}{2}}\ln {\boldsymbol {C}}^{e}\,.}$

Симметризованный Стресс Манделя тензор является удобной мерой напряжения для конечной пластичности и определяется как

${\displaystyle {\boldsymbol {M}}:={\tfrac {1}{2}}({\boldsymbol {C}}^{e}\cdot {\boldsymbol {S}}+{\boldsymbol {S}}\cdot {\boldsymbol {C}}^{e})}$

куда S это второй стресс Пиолы-Кирхгофа. Возможная гиперупругая модель с точки зрения логарифмической деформации: ^[6]

${\displaystyle {\boldsymbol {M}}={\frac {\partial W}{\partial {\boldsymbol {E}}^{e}}}=J\,{\frac {dU}{dJ}}+2\mu \,{\text{dev}}({\boldsymbol {E}}^{e})}$

куда W - функция плотности энергии деформации, J = det (F), μ представляет собой модуль, а «dev» указывает девиаторную часть тензора.

Правило потока

Применение Неравенство Клаузиуса-Дюгема приводит, в отсутствие пластического спина, к правилу потока конечной деформации

${\displaystyle {\boldsymbol {D}}^{p}={\dot {\lambda }}\,{\frac {\partial f}{\partial {\boldsymbol {M}}}}\,.}$

Условия погрузки-разгрузки

Можно показать, что условия загрузки-разгрузки эквивалентны Условия Каруша-Куна-Такера

${\displaystyle {\dot {\lambda }}\geq 0~,~~f\leq 0~,~~{\dot {\lambda }}\,f=0\,.}$

Условие согласованности

Условие консистенции такое же, как и для случая малой деформации,

${\displaystyle {\dot {\lambda }}\,{\dot {f}}=0\,.}$

Рекомендации

1. Люблинер, Яков (2008), Теория пластичности, Courier Dover Publications.
2. Анандараджа (2010).
3. Bilby, B.A .; Bullough, R .; Смит, Э. (1955), "Непрерывные распределения дислокаций: новое применение методов неримановой геометрии", Труды Королевского общества А, 231 (1185): 263–273, Bibcode:1955RSPSA.231..263B, Дои:10.1098 / rspa.1955.0171
4. Крёнер, Э. (1958), "Kontinuumstheorie der Versetzungen und Eigenspannungen", Эрг. Энгью. Математика., 5: 1–179
5. Ли, Э. Х. (1969), «Упруго-пластическая деформация при конечных деформациях» (PDF), Журнал прикладной механики, 36 (1): 1–6, Bibcode:1969JAM .... 36 .... 1л, Дои:10.1115/1.3564580^{[постоянная мертвая ссылка ]}
6. Ананд, Л. (1979), "О приближенной функции деформации-энергии Х. Хенки для умеренных деформаций", Журнал прикладной механики, 46 (1): 78–82, Bibcode:1979JAM .... 46 ... 78A, Дои:10.1115/1.3424532

Смотрите также

• Пластичность (физика)