Код исправления ошибок - Error correction code

"Interleaver" перенаправляется сюда. Для оптоволоконного устройства см. оптический перемежитель.

В вычисление, телекоммуникации, теория информации, и теория кодирования, код исправления ошибок, иногда код исправления ошибок, (ECC) используется для контроль ошибок в данных из-за ненадежных или зашумленных каналы связи.[1][2] Основная идея заключается в том, что отправитель кодирует сообщение с помощью избыточная информация в виде ECC. Избыточность позволяет получателю обнаруживать ограниченное количество ошибок, которые могут возникать в любом месте сообщения, и часто исправлять эти ошибки без повторной передачи. Американский математик Ричард Хэмминг пионером в этой области в 1940-х годах и изобрел первый исправляющий ошибки код в 1950 году: Код Хэмминга (7,4).[2]

ECC контрастирует с обнаружение ошибок в том, что возникающие ошибки могут быть исправлены, а не просто обнаружены. Преимущество состоит в том, что система, использующая ECC, не требует обратный канал для запроса повторной передачи данных при возникновении ошибки. Обратной стороной является то, что к сообщению добавляются фиксированные накладные расходы, что требует более высокой полосы пропускания прямого канала. Таким образом, ECC применяется в ситуациях, когда повторные передачи являются дорогостоящими или невозможными, например, при односторонних каналах связи и при передаче на несколько приемников в многоадресная передача. Соединения с длительной задержкой также выигрывают; в случае спутника на орбите вокруг Уран, повторная передача из-за ошибок может вызвать задержку в пять часов. Информация ECC обычно добавляется к массовое хранилище устройства для восстановления поврежденных данных, широко используются в модемы, и используется в системах, где основная память Память ECC.

Обработка ECC в приемнике может применяться к цифровому потоку битов или при демодуляции несущей с цифровой модуляцией. Для последних ECC является неотъемлемой частью исходного аналого-цифровое преобразование в приемнике. В Декодер Витерби реализует алгоритм мягкого решения демодулировать цифровые данные из аналогового сигнала, искаженного шумом. Многие кодеры / декодеры ECC также могут генерировать коэффициент битовых ошибок (BER) сигнал, который можно использовать в качестве обратной связи для точной настройки аналоговой принимающей электроники.

Максимальная доля ошибок или пропущенных битов, которые могут быть исправлены, определяется конструкцией кода ECC, поэтому разные коды исправления ошибок подходят для разных условий. Как правило, более сильный код вызывает большую избыточность, которую необходимо передавать с использованием доступной полосы пропускания, что снижает эффективную скорость передачи данных при одновременном улучшении принимаемого эффективного отношения сигнал / шум. В теорема кодирования с шумом из Клод Шеннон отвечает на вопрос о том, сколько полосы пропускания осталось для передачи данных при использовании наиболее эффективного кода, который обращает вероятность ошибки декодирования в ноль. Это устанавливает границы теоретической максимальной скорости передачи информации канала с некоторым заданным базовым уровнем шума. Однако это доказательство неконструктивно и, следовательно, не дает представления о том, как создать код, обеспечивающий производительность. После многих лет исследований некоторые современные системы ECC[когда? ] очень близко подошли к теоретическому максимуму.

Прямое исправление ошибок

В телекоммуникации, теория информации, и теория кодирования, упреждающее исправление ошибок (FEC) или же кодирование каналов[3][4] это техника, используемая для контроль ошибок в передача данных чрезмерно ненадежный или шумный каналы связи. Основная идея заключается в том, что отправитель кодирует сообщение в избыточный Кстати, чаще всего с помощью ECC.

Избыточность позволяет получателю обнаруживать ограниченное количество ошибок, которые могут возникнуть в любом месте сообщения, и часто исправлять эти ошибки без повторной передачи. FEC дает приемнику возможность исправлять ошибки без необходимости обратный канал для запроса повторной передачи данных, но за счет фиксированной более высокой пропускной способности прямого канала. Поэтому FEC применяется в ситуациях, когда повторная передача является дорогостоящей или невозможной, например, при односторонних каналах связи и при передаче на несколько приемников в многоадресная передача. Информация FEC обычно добавляется к массовое хранилище (магнитные, оптические и твердотельные / флэш-устройства) устройства для восстановления поврежденных данных, широко используются в модемы, используется в системах, где основная память Память ECC и в ситуациях широковещательной передачи, когда приемник не имеет возможности запрашивать повторную передачу или это может вызвать значительную задержку. Например, в случае спутника на орбите вокруг Уран повторная передача из-за ошибок декодирования может привести к задержке не менее 5 часов.

Обработка FEC в приемнике может применяться к цифровому битовому потоку или при демодуляции несущей с цифровой модуляцией. Для последнего FEC является неотъемлемой частью исходного аналого-цифровое преобразование в приемнике. В Декодер Витерби реализует алгоритм мягкого решения демодулировать цифровые данные из аналогового сигнала, искаженного шумом. Многие кодеры FEC также могут генерировать коэффициент битовых ошибок (BER) сигнал, который можно использовать в качестве обратной связи для точной настройки аналоговой принимающей электроники.

Максимальная доля ошибок или недостающих битов, которые могут быть исправлены, определяется конструкцией ECC, поэтому для различных условий подходят разные коды прямого исправления ошибок. Как правило, более сильный код вызывает большую избыточность, которую необходимо передавать с использованием доступной полосы пропускания, что снижает эффективную скорость передачи данных при одновременном улучшении принимаемого эффективного отношения сигнал / шум. В теорема кодирования с шумом Клода Шеннона отвечает на вопрос о том, сколько полосы пропускания остается для передачи данных при использовании наиболее эффективного кода, который сводит вероятность ошибки декодирования к нулю. Это устанавливает границы теоретической максимальной скорости передачи информации канала с некоторым заданным базовым уровнем шума. Его доказательство неконструктивно и, следовательно, не дает понимания того, как создать код, обеспечивающий производительность. Однако после многих лет исследований некоторые передовые системы FEC, такие как полярный код[4] достичь пропускной способности канала Шеннона в рамках гипотезы кадра бесконечной длины.

Как это устроено

ECC достигается путем добавления избыточность к передаваемой информации с помощью алгоритма. Избыточный бит может быть сложной функцией многих исходных информационных битов. Исходная информация может появляться или не появляться буквально в закодированном выводе; коды, которые включают неизмененный ввод в вывод, являются систематический, а те, кто этого не делает, несистематический.

Упрощенным примером ECC является передача каждого бита данных 3 раза, что известно как (3,1) код повторения. Через шумный канал приемник может видеть 8 вариантов вывода, см. Таблицу ниже.

Триплет получилИнтерпретируется как
0000 (без ошибок)
0010
0100
1000
1111 (без ошибок)
1101
1011
0111

Это позволяет исправить ошибку в любой из трех выборок «большинством голосов» или «демократическим голосованием». Корректирующая способность этого ECC:

  • Ошибка до 1 бита триплета, или
  • пропущено до 2 битов триплета (случаи не показаны в таблице).

Несмотря на простоту реализации и широкое использование, этот тройное модульное резервирование это относительно неэффективный ECC. Более совершенные коды ECC обычно проверяют несколько последних десятков или даже несколько последних сотен ранее принятых битов, чтобы определить, как декодировать текущую небольшую группу битов (обычно в группах от 2 до 8 бит).

Усреднение шума для уменьшения ошибок

Можно сказать, что ECC работает путем «усреднения шума»; поскольку каждый бит данных влияет на многие передаваемые символы, искажение одних символов шумом обычно позволяет извлекать исходные пользовательские данные из других, неповрежденных принятых символов, которые также зависят от тех же пользовательских данных.

  • Из-за этого эффекта «объединения рисков» цифровые системы связи, использующие ECC, как правило, работают намного выше определенного минимума. соотношение сигнал шум и совсем не ниже.
  • Этот тенденция "все или ничего" - в эффект обрыва - становится более выраженным по мере использования более сильных кодов, более приближенных к теоретическим Предел Шеннона.
  • Перемежение данных, закодированных с помощью ЕСС, может уменьшить свойства "все или ничего" переданных кодов ЕСС, когда ошибки канала имеют тенденцию возникать в пакетах. Однако у этого метода есть ограничения; его лучше всего использовать для узкополосных данных.

Большинство телекоммуникационных систем используют фиксированный код канала разработан, чтобы выдержать ожидаемый худший случай частота ошибок по битам, а затем вообще перестают работать, если частота ошибок по битам становится еще хуже. Однако некоторые системы адаптируются к данным условиям ошибки канала: некоторые экземпляры гибридный автоматический повторный запрос используйте фиксированный метод ECC, если ECC может обрабатывать частоту ошибок, затем переключитесь на ARQ когда частота ошибок становится слишком высокой;адаптивная модуляция и кодирование использует различные скорости ECC, добавляя больше битов исправления ошибок на пакет, когда в канале более высокая частота ошибок, или удаляя их, когда они не нужны.

Типы ECC

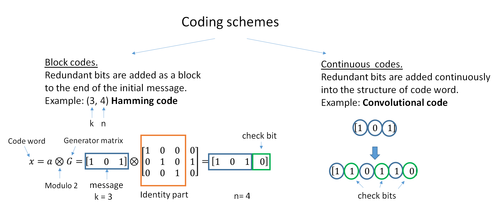
Основные статьи: Код блокировки и Сверточный код
Краткая классификация кодов исправления ошибок.

Две основные категории кодов ECC: блочные коды и сверточные коды.

  • Блочные коды работают с блоками (пакетами) фиксированного размера, состоящими из битов или символов заранее определенного размера. Практические блочные коды обычно могут быть жестко декодированы в полиномиальное время к их длине блока.
  • Сверточные коды работают с битовыми или символьными потоками произвольной длины. Чаще всего они софт-декодируются Алгоритм Витерби, хотя иногда используются и другие алгоритмы. Декодирование Витерби обеспечивает асимптотически оптимальную эффективность декодирования при увеличении длины ограничения сверточного кода, но за счет экспоненциально возрастающая сложность. Завершенный сверточный код также является «блочным кодом» в том смысле, что он кодирует блок входных данных, но размер блока сверточного кода, как правило, произвольный, в то время как блочные коды имеют фиксированный размер, определяемый их алгебраическими характеристиками. Типы завершения для сверточных кодов включают «концевую передачу» и «сброс битов».

Есть много типов блочных кодов; Кодирование Рида-Соломона примечателен своим широким использованием в компакт-диски, DVD, и жесткие диски. Другие примеры классических блочных кодов включают Голай, BCH, Многомерная четность, и Коды Хэмминга.

ECC Хэмминга обычно используется для исправления NAND flash ошибки памяти.[5]Это обеспечивает исправление однобитовых ошибок и обнаружение 2-битных ошибок. Коды Хамминга подходят только для более надежных одноуровневая ячейка (SLC) NAND.Denser многоуровневая ячейка (MLC) NAND может использовать многобитовый корректирующий ECC, такой как BCH или Reed-Solomon.[6][7] NOR Flash обычно не использует исправление ошибок.[6]

Классические блочные коды обычно декодируются с использованием трудное решение алгоритмы,[8] Это означает, что для каждого входного и выходного сигнала принимается жесткое решение, соответствует ли он единице или нулю. Напротив, сверточные коды обычно декодируются с использованием мягкое решение алгоритмы, такие как Витерби, MAP или BCJR алгоритмы, обрабатывающие (дискретизированные) аналоговые сигналы и обеспечивающие гораздо более высокую производительность исправления ошибок, чем декодирование с жестким решением.

Почти все классические блочные коды применяют алгебраические свойства конечные поля. Поэтому классические блочные коды часто называют алгебраическими кодами.

В отличие от классических блочных кодов, которые часто определяют способность к обнаружению или исправлению ошибок, многие современные блочные коды, такие как Коды LDPC таких гарантий нет. Вместо этого современные коды оцениваются с точки зрения их частоты ошибок по битам.

Наиболее упреждающее исправление ошибок коды исправляют только перевороты битов, но не вставки или удаления битов. Расстояние Хэмминга является подходящим способом измерения частота ошибок по битам.Некоторые коды прямого исправления ошибок предназначены для исправления вставки и удаления битов, например коды маркеров и коды водяных знаков. Расстояние Левенштейна - более подходящий способ измерения частоты ошибок по битам при использовании таких кодов.[9]

Кодовая скорость и компромисс между надежностью и скоростью передачи данных

Смотрите также: Битрейт § Скорость передачи информации

Фундаментальный принцип ECC - добавить избыточные биты, чтобы помочь декодеру узнать истинное сообщение, закодированное передатчиком. Кодовая скорость данной системы ЕСС определяется как соотношение между количеством информационных битов и общим количеством битов (то есть информацией плюс биты избыточности) в данном коммуникационном пакете. Кодовая скорость, следовательно, является действительным числом. Низкая кодовая скорость, близкая к нулю, подразумевает сильный код, который использует много избыточных битов для достижения хорошей производительности, тогда как большая кодовая скорость, близкая к 1, подразумевает слабый код.

Избыточные биты, защищающие информацию, должны передаваться с использованием тех же коммуникационных ресурсов, которые они пытаются защитить. Это вызывает фундаментальный компромисс между надежностью и скоростью передачи данных.[10] В одном крайнем случае, сильный код (с низкой кодовой скоростью) может вызвать значительное увеличение SNR приемника (отношения сигнал / шум), уменьшая частоту ошибок по битам, за счет снижения эффективной скорости передачи данных. С другой стороны, без использования какого-либо ECC (то есть кодовой скорости, равной 1) используется полный канал для целей передачи информации за счет того, что биты остаются без какой-либо дополнительной защиты.

Один интересный вопрос заключается в следующем: насколько эффективным с точки зрения передачи информации может быть ECC, который имеет незначительную частоту ошибок декодирования? На этот вопрос ответил Клод Шеннон со своей второй теоремой, которая гласит, что пропускная способность канала - это максимальная скорость передачи данных, достижимая любым ECC, частота ошибок которого стремится к нулю:[11] Его доказательство опирается на гауссовское случайное кодирование, которое не подходит для реальных приложений. Верхняя граница, заданная работой Шеннона, вдохновила на долгий путь к разработке ECC, которые могут приблизиться к пределу конечных характеристик. Различные коды сегодня могут достигать почти предела Шеннона. Однако ECC, обеспечивающие пропускную способность, обычно чрезвычайно сложно реализовать.

Наиболее популярные ECC имеют компромисс между производительностью и вычислительной сложностью. Обычно их параметры дают диапазон возможных кодовых скоростей, которые можно оптимизировать в зависимости от сценария. Обычно эта оптимизация выполняется для достижения низкой вероятности ошибки декодирования при минимальном влиянии на скорость передачи данных. Другим критерием оптимизации кодовой скорости является баланс между низкой частотой ошибок и количеством повторных передач с учетом затрат энергии на связь.[12]

Составные коды ECC для повышения производительности

Основная статья: Составные коды исправления ошибок

Классические (алгебраические) блочные коды и сверточные коды часто комбинируются в соединенный схемы кодирования, в которых сверточный код с короткой ограниченной длиной, декодированный по Витерби, выполняет большую часть работы, а блочный код (обычно Рида-Соломона) с большим размером символа и длиной блока «стирает» любые ошибки, сделанные сверточным декодером. Однопроходное декодирование с использованием этого семейства кодов с исправлением ошибок может дать очень низкий уровень ошибок, но для условий передачи на большие расстояния (например, в глубоком космосе) рекомендуется итеративное декодирование.

Составные коды стали стандартной практикой в ​​спутниковой связи и связи в дальнем космосе с тех пор, как Вояджер 2 впервые применил эту технику во время встречи в 1986 году с Уран. В Галилео craft использовал итеративные сцепленные коды для компенсации условий с очень высокой частотой ошибок, вызванных неисправностью антенны.

Проверка четности с низкой плотностью (LDPC)

Основная статья: Код проверки на четность с низкой плотностью

Проверка четности с низкой плотностью (LDPC) коды - это класс высокоэффективных линейных блочных кодов, состоящих из множества кодов одиночной проверки на четность (SPC). Они могут обеспечить производительность, очень близкую к пропускная способность канала (теоретический максимум) с использованием подхода итеративного декодирования с мягким решением при линейной временной сложности с точки зрения длины их блока. Практические реализации в значительной степени полагаются на параллельное декодирование составляющих кодов SPC.

Коды LDPC были впервые введены Роберт Г. Галлагер защитил кандидатскую диссертацию в 1960 году, но из-за вычислительных затрат на реализацию кодировщика и декодера и внедрения Рид – Соломон коды, они в основном игнорировались до 1990-х годов.

Коды LDPC теперь используются во многих последних стандартах высокоскоростной связи, таких как DVB-S2 (Цифровое видеовещание - спутник - второе поколение), WiMAX (IEEE 802.16e стандарт для микроволновой связи), High-Speed ​​Wireless LAN (IEEE 802.11n ),[13] 10GBase-T Ethernet (802.3an) и G.hn/G.9960 (Стандарт ITU-T для сетей по линиям электропередач, телефонным линиям и коаксиальному кабелю). Другие коды LDPC стандартизированы для стандартов беспроводной связи в пределах 3GPP MBMS (видеть коды фонтанов ).

Турбо коды

Основная статья: Турбо код

Турбо кодирование представляет собой итеративную схему мягкого декодирования, которая объединяет два или более относительно простых сверточных кода и перемежитель для создания блочного кода, который может работать с точностью до доли децибела Предел Шеннона. Хищничество Коды LDPC с точки зрения практического применения теперь они обеспечивают аналогичную производительность.

Одним из первых коммерческих приложений турбо-кодирования было CDMA2000 1x (TIA IS-2000) цифровая сотовая технология, разработанная Qualcomm и продано Verizon Wireless, Спринт, и другие перевозчики. Он также используется для развития CDMA2000 1x специально для доступа в Интернет, 1xEV-DO (TIA IS-856). Как и 1x, EV-DO был разработан Qualcomm, и продается Verizon Wireless, Спринт, и другие операторы (маркетинговое название Verizon для 1xEV-DO - Широкополосный доступ, Потребительские и бизнес-маркетинговые названия Sprint для 1xEV-DO: Power Vision и Мобильного широкополосного доступа, соответственно).

Локальное декодирование и тестирование кодов

Основные статьи: Локально декодируемый код и Локально тестируемый код

Иногда необходимо декодировать только отдельные биты сообщения или проверить, является ли данный сигнал кодовым словом, и сделать это, не глядя на весь сигнал. Это может иметь смысл в настройке потоковой передачи, где кодовые слова слишком велики для того, чтобы их можно было классически декодировать достаточно быстро, и где на данный момент интересны только несколько битов сообщения. Также такие коды стали важным инструментом в теория сложности вычислений, например, для дизайна вероятностно проверяемые доказательства.

Локально декодируемые коды представляют собой коды с исправлением ошибок, для которых отдельные биты сообщения могут быть восстановлены с вероятностью только путем просмотра небольшого (скажем, постоянного) числа позиций кодового слова, даже после того, как кодовое слово было искажено в некоторой постоянной доле позиций. Локально тестируемые коды являются кодами с исправлением ошибок, для которых можно вероятностно проверить, близок ли сигнал к кодовому слову, только посмотрев на небольшое количество позиций сигнала.

Чередование

"Interleaver" перенаправляется сюда. Для оптоволоконного устройства см. оптический перемежитель.
Краткая иллюстрация идеи чередования.

Перемежение часто используется в цифровых системах связи и хранения данных для повышения производительности кодов прямого исправления ошибок. Много каналы связи не без памяти: ошибки обычно возникают в всплески а не самостоятельно. Если количество ошибок в кодовое слово превышает возможности кода исправления ошибок, он не может восстановить исходное кодовое слово. Чередование облегчает эту проблему, перетасовывая исходные символы по нескольким кодовым словам, тем самым создавая более равномерное распределение ошибок.[14] Поэтому перемежение широко используется для пакетное исправление ошибок.

Анализ современных итерационных кодов, таких как турбокоды и Коды LDPC, обычно предполагает независимое распределение ошибок.[15] Поэтому системы, использующие коды LDPC, обычно используют дополнительное перемежение символов в кодовом слове.[16]

Для турбокодов перемежитель является неотъемлемым компонентом, и его правильная конструкция имеет решающее значение для хорошей производительности.[14][17] Алгоритм итеративного декодирования работает лучше всего, когда нет коротких циклов в факторный график что представляет собой декодер; перемежитель выбран, чтобы избежать коротких циклов.

Конструкции перемежителя включают:

  • прямоугольные (или однородные) перемежители (аналогично методу с использованием коэффициентов пропуска, описанному выше)
  • сверточные перемежители
  • случайные перемежители (где перемежитель - известная случайная перестановка)
  • S-случайный перемежитель (где перемежитель - это известная случайная перестановка с ограничением, что никакие входные символы на расстоянии S не появляются на расстоянии S на выходе).[18]
  • бесконфликтный квадратичный перестановочный многочлен (QPP).[19] Пример использования находится в Долгосрочное развитие 3GPP стандарт мобильной связи.[20]

В мульти-перевозчик системы связи, перемежение по несущим может использоваться для обеспечения частоты разнообразие, например, чтобы смягчить частотно-избирательное замирание или узкополосные помехи.[21]

Пример

Передача без чередования:

Сообщение без ошибок: aaaabbbbccccddddeeeeffffggggПередача с ошибкой пакета: aaaabbbbccc____deeeeffffgggg

Здесь каждая группа одинаковых букв представляет 4-битовое однобитовое кодовое слово с исправлением ошибок. Кодовое слово cccc изменяется в один бит и может быть исправлено, но кодовое слово dddd изменяется в трех битах, поэтому либо оно не может быть декодировано вообще, либо может быть декодировано неправильно.

С чередованием:

Безошибочные кодовые слова: aaaabbbbccccddddeeeeffffggggInterleaved: abcdefgabcdefgabcdefgabcdefgПередача с пакетной ошибкой: abcdefgabcd____bcdefgabcdefg Полученные кодовые слова после деинтерлейвингаccccc_dee_defbb

В каждом из кодовых слов «aaaa», «eeee», «ffff» и «gggg» изменяется только один бит, поэтому однобитовый код с исправлением ошибок все декодирует правильно.

Передача без чередования:

Исходное переданное предложение: ThisIsAnExampleOfInterleaving Полученное предложение с ошибкой пакета: ThisIs______pleOfInterleaving

Термин «пример» в большинстве случаев оказывается непонятным и трудным для исправления.

С чередованием:

Переданное предложение: ThisIsAnExampleOfInterleaving ... Безошибочная передача: TIEpfeaghsxlIrv.iAaenli.snmOten.Получено предложение с пакетной ошибкой: TIEpfe ______ Irv.iAaenli.snmOten.Получено предложение после деинтерлейвинга: _T_isI_A

Ни одно слово не потеряно полностью, а недостающие буквы можно восстановить с минимальными догадками.

Недостатки чередования

Использование техники перемежения увеличивает общую задержку. Это связано с тем, что весь перемежаемый блок должен быть принят до того, как пакеты можно будет декодировать.[22] Также перемежители скрывают структуру ошибок; без перемежителя более продвинутые алгоритмы декодирования могут воспользоваться структурой ошибок и обеспечить более надежную связь, чем более простой декодер в сочетании с перемежителем[нужна цитата ]. Пример такого алгоритма основан на нейронная сеть[23] конструкции.

Программное обеспечение для кодов исправления ошибок

Моделирование поведения кодов исправления ошибок (ECC) в программном обеспечении - обычная практика для разработки, проверки и улучшения ECC. Предстоящий стандарт беспроводной связи 5G открывает новый диапазон приложений для программных ECC: Облачные сети радиодоступа (C-RAN) в Программно-определяемое радио (SDR) контекст. Идея состоит в том, чтобы напрямую использовать программные ECC в коммуникациях. Например, в 5G программные ECC могут быть расположены в облаке, а антенны могут быть подключены к этим вычислительным ресурсам: таким образом повышается гибкость сети связи и, в конечном итоге, повышается энергоэффективность системы.

В этом контексте существует различное доступное программное обеспечение с открытым исходным кодом, перечисленное ниже (не является исчерпывающим).

  • AFF3CT (A Fast Forward Error Correction Toolbox): полная коммуникационная цепочка на C ++ (многие поддерживаемые коды, такие как Turbo, LDPC, полярные коды и т. Д.), Очень быстрая и специализированная на канальном кодировании (может использоваться как программа для моделирования или как библиотека для SDR).
  • IT ++: библиотека классов и функций C ++ для линейной алгебры, численной оптимизации, обработки сигналов, связи и статистики.
  • Под открытым небом: реализация (на языке C) спецификаций 3GPP, касающихся Evolved Packet Core Networks.

Список кодов исправления ошибок

РасстояниеКод
2 (обнаружение одиночной ошибки)Паритет
3 (исправление одиночных ошибок)Тройное модульное резервирование
3 (исправление одиночных ошибок)идеальный Хэмминг, такой как Хэмминга (7,4)
4 (ОТДЕЛЕННЫЙ )Расширенный Хэмминга
5 (исправление двойной ошибки)
6 (исправление двойной ошибки / обнаружение тройной ошибки)
7 (исправление трех ошибок)идеально двоичный код Голея
8 (ТЕКФЕД)расширенный двоичный код Голея

Смотрите также

Рекомендации

  1. ^ Гловер, Нил; Дадли, Трент (1990). Практический дизайн коррекции ошибок для инженеров (Редакция 1.1, 2-е изд.). Колорадо, США: Cirrus Logic. ISBN  0-927239-00-0. ISBN  978-0-927239-00-4.
  2. ^ а б Хэмминг, Р. У. (апрель 1950 г.). «Коды обнаружения и исправления ошибок». Технический журнал Bell System. СОЕДИНЕННЫЕ ШТАТЫ АМЕРИКИ: AT&T. 29 (2): 147–160. Дои:10.1002 / j.1538-7305.1950.tb00463.x.
  3. ^ Чарльз Ван; Дин Скляр; Дайана Джонсон (зима 2001–2002 гг.). «Кодирование с прямым исправлением ошибок». Сшивка. Аэрокосмическая корпорация. 3 (1). Архивировано из оригинал 25 февраля 2012 г.. Получено 5 марта 2006. Как работают коды прямого исправления ошибок
  4. ^ а б Маундер, Роберт (2016). «Обзор кодирования каналов».
  5. ^ «Коды Хэмминга для устройств флэш-памяти NAND». EE Times-Asia. Видимо на основе "Техническое примечание Micron TN-29-08: Коды Хэмминга для устройств флэш-памяти NAND". 2005. Оба говорят: «Алгоритм Хэмминга - это признанный в отрасли метод обнаружения и исправления ошибок во многих приложениях на базе флэш-памяти SLC NAND».
  6. ^ а б «Какие типы ECC следует использовать во флэш-памяти?» (Примечание по применению). Размах. 2011 г. Как алгоритм Рида-Соломона, так и алгоритм BCH являются общими вариантами ECC для флэш-памяти MLC NAND. ... Блочные коды на основе Хэмминга являются наиболее часто используемыми ECC для SLC .... и Рида-Соломона, и BCH могут обрабатывать множественные ошибки и широко используются во флэш-памяти MLC.
  7. ^ Джим Кук (август 2007 г.). «Неудобная правда флэш-памяти NAND» (PDF). п. 28. Для SLC достаточно кода с порогом коррекции 1. t = 4 требуется ... для MLC.
  8. ^ Балди, М .; Chiaraluce, F. (2008). «Простая схема для декодирования распространения убеждений кодов BCH и RS в мультимедийных передачах». Международный журнал цифрового мультимедийного вещания. 2008: 1–12. Дои:10.1155/2008/957846.
  9. ^ Шах, Гаурав; Молина, Андрес; Пламя, Мэтт (2006). «Клавиатуры и скрытые каналы». USENIX. Получено 20 декабря 2018.
  10. ^ Це, Давид; Вишванатх, Прамод (2005), Основы беспроводной связи, Издательство Кембриджского университета, ВЕЛИКОБРИТАНИЯ
  11. ^ Шеннон, К. Э. (1948). «Математическая теория коммуникации» (PDF). Технический журнал Bell System. 27 (3–4): 379–423 & 623–656. Дои:10.1002 / j.1538-7305.1948.tb01338.x.
  12. ^ Rosas, F .; Brante, G .; Souza, R.D .; Оберли, К. (2014). «Оптимизация кодовой скорости для достижения энергоэффективной беспроводной связи». Материалы конференции по беспроводной связи и сети IEEE (WCNC).
  13. ^ Стандарт IEEE, раздел 20.3.11.6 «802.11n-2009», IEEE, 29 октября 2009 г., по состоянию на 21 марта 2011 г.
  14. ^ а б Vucetic, B .; Юань, Дж. (2000). Турбокоды: принципы и применение. Springer Verlag. ISBN  978-0-7923-7868-6.
  15. ^ Луби, Майкл; Митценмахер, М .; Shokrollahi, A .; Spielman, D .; Стеманн, В. (1997). «Практические безнадежные коды». Proc. 29-е ежегодное Ассоциация вычислительной техники (ACM) Симпозиум по теории вычислений.
  16. ^ «Цифровое видеовещание (DVB); структура кадра второго поколения, системы кодирования каналов и модуляции для вещания, интерактивных услуг, сбора новостей и других приложений спутниковой широкополосной связи (DVB-S2)». En 302 307. ETSI (V1.2.1). Апрель 2009 г.
  17. ^ Эндрюс, К. С .; Divsalar, D .; Долинар, С .; Hamkins, J .; Jones, C.R .; Поллара, Ф. (ноябрь 2007 г.). «Разработка кодов Turbo и LDPC для приложений дальнего космоса». Труды IEEE. 95 (11): 2142–2156. Дои:10.1109 / JPROC.2007.905132.
  18. ^ Долинар, С .; Дивсалар, Д. (15 августа 1995 г.). «Распределение весов для турбо-кодов с использованием случайных и неслучайных перестановок». Отчет о проделанной работе TDA: 42–122. CiteSeerX  10.1.1.105.6640.
  19. ^ Такешита, Оскар (2006). "Перемежители полиномов с перестановками: алгебро-геометрическая перспектива". IEEE Transactions по теории информации. 53 (6): 2116–2132. arXiv:cs / 0601048. Дои:10.1109 / TIT.2007.896870.
  20. ^ 3GPP TS 36.212, версия 8.8.0, стр. 14
  21. ^ «Цифровое видеовещание (DVB); структура кадра, кодирование каналов и модуляция для системы цифрового наземного телевизионного вещания второго поколения (DVB-T2)». En 302 755. ETSI (V1.1.1). Сентябрь 2009 г.
  22. ^ Techie (3 июня 2010 г.). "Объяснение чередования". Блог W3 Techie. Получено 3 июн 2010.
  23. ^ Крастанов, Стефан; Цзян, Лян (8 сентября 2017 г.). «Вероятностный декодер глубинной нейронной сети для кодов стабилизатора». Научные отчеты. 7 (1): 1–7. Дои:10.1038 / s41598-017-11266-1.
  24. ^ Перри, Джонатан; Балакришнан, Хари; Шах, Деваврат (2011). "Бесчисленные спинномозговые коды". Материалы 10-го семинара ACM по горячим темам в сетях. Дои:10.1145/2070562.2070568. HDL:1721.1/79676.

дальнейшее чтение

внешняя ссылка