Del в цилиндрических и сферических координатах - Del in cylindrical and spherical coordinates

Это список некоторых векторное исчисление формулы для работы с общими криволинейный системы координат.

Примечания

• В этой статье используются стандартные обозначения ISO 80000-2, который заменяет ISO 31-11, за сферические координаты (другие источники могут перевернуть определения θ и φ):
  • Полярный угол обозначается θ: это угол между z-ось и радиальный вектор, соединяющий начало координат с рассматриваемой точкой.
  • Азимутальный угол обозначается как φ: это угол между Икс-оси и проекции радиального вектора на ху-самолет.
• Функция atan2 (у, Икс) можно использовать вместо математической функции арктан (у/Икс) благодаря домен и изображение. Классическая функция arctan имеет образ (−π / 2, + π / 2), тогда как atan2 определяется как изображение (−π, π].

Координатные преобразования

Преобразование декартовых, цилиндрических и сферических координат^[1]

		Из
		Декартово	Цилиндрический	Сферический
К	Декартово	${\displaystyle {\begin{aligned}x&=x\\y&=y\\z&=z\end{aligned}}}$	${\displaystyle {\begin{aligned}x&=\rho \cos \varphi \\y&=\rho \sin \varphi \\z&=z\end{aligned}}}$	${\displaystyle {\begin{aligned}x&=r\sin \theta \cos \varphi \\y&=r\sin \theta \sin \varphi \\z&=r\cos \theta \end{aligned}}}$
	Цилиндрический	${\displaystyle {\begin{aligned}\rho &={\sqrt {x^{2}+y^{2}}}\\\varphi &=\arctan \left({\frac {y}{x}}\right)\\z&=z\end{aligned}}}$	${\displaystyle {\begin{aligned}\rho &=\rho \\\varphi &=\varphi \\z&=z\end{aligned}}}$	${\displaystyle {\begin{aligned}\rho &=r\sin \theta \\\varphi &=\varphi \\z&=r\cos \theta \end{aligned}}}$
	Сферический	${\displaystyle {\begin{aligned}r&={\sqrt {x^{2}+y^{2}+z^{2}}}\\\theta &=\arctan \left({\frac {\sqrt {x^{2}+y^{2}}}{z}}\right)\\\varphi &=\arctan \left({\frac {y}{x}}\right)\end{aligned}}}$	${\displaystyle {\begin{aligned}r&={\sqrt {\rho ^{2}+z^{2}}}\\\theta &=\arctan {\left({\frac {\rho }{z}}\right)}\\\varphi &=\varphi \end{aligned}}}$	${\displaystyle {\begin{aligned}r&=r\\\varphi &=\varphi \\\theta &=\theta \\\end{aligned}}}$

Преобразования единичных векторов

Преобразование единичных векторов в декартовой, цилиндрической и сферической системах координат с точки зрения пункт назначения координаты^[1]

	Декартово	Цилиндрический	Сферический
Декартово	Нет данных	${\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&=\cos \varphi {\hat {\boldsymbol {\rho }}}-\sin \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {y} }}&=\sin \varphi {\hat {\boldsymbol {\rho }}}+\cos \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}}$	${\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&=\sin \theta \cos \varphi {\hat {\mathbf {r} }}+\cos \theta \cos \varphi {\hat {\boldsymbol {\theta }}}-\sin \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {y} }}&=\sin \theta \sin \varphi {\hat {\mathbf {r} }}+\cos \theta \sin \varphi {\hat {\boldsymbol {\theta }}}+\cos \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&=\cos \theta {\hat {\mathbf {r} }}-\sin \theta {\hat {\boldsymbol {\theta }}}\end{aligned}}}$
Цилиндрический	${\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&={\frac {x{\hat {\mathbf {x} }}+y{\hat {\mathbf {y} }}}{\sqrt {x^{2}+y^{2}}}}\\{\hat {\boldsymbol {\varphi }}}&={\frac {-y{\hat {\mathbf {x} }}+x{\hat {\mathbf {y} }}}{\sqrt {x^{2}+y^{2}}}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}}$	Нет данных	${\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&=\sin \theta {\hat {\mathbf {r} }}+\cos \theta {\hat {\boldsymbol {\theta }}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&=\cos \theta {\hat {\mathbf {r} }}-\sin \theta {\hat {\boldsymbol {\theta }}}\end{aligned}}}$
Сферический	${\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&={\frac {x{\hat {\mathbf {x} }}+y{\hat {\mathbf {y} }}+z{\hat {\mathbf {z} }}}{\sqrt {x^{2}+y^{2}+z^{2}}}}\\{\hat {\boldsymbol {\theta }}}&={\frac {\left(x{\hat {\mathbf {x} }}+y{\hat {\mathbf {y} }}\right)z-\left(x^{2}+y^{2}\right){\hat {\mathbf {z} }}}{{\sqrt {x^{2}+y^{2}+z^{2}}}{\sqrt {x^{2}+y^{2}}}}}\\{\hat {\boldsymbol {\varphi }}}&={\frac {-y{\hat {\mathbf {x} }}+x{\hat {\mathbf {y} }}}{\sqrt {x^{2}+y^{2}}}}\end{aligned}}}$	${\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&={\frac {\rho {\hat {\boldsymbol {\rho }}}+z{\hat {\mathbf {z} }}}{\sqrt {\rho ^{2}+z^{2}}}}\\{\hat {\boldsymbol {\theta }}}&={\frac {z{\hat {\boldsymbol {\rho }}}-\rho {\hat {\mathbf {z} }}}{\sqrt {\rho ^{2}+z^{2}}}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\end{aligned}}}$	Нет данных

Преобразование единичных векторов в декартовой, цилиндрической и сферической системах координат с точки зрения источник координаты

	Декартово	Цилиндрический	Сферический
Декартово	Нет данных	${\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&={\frac {x{\hat {\boldsymbol {\rho }}}-y{\hat {\boldsymbol {\varphi }}}}{\sqrt {x^{2}+y^{2}}}}\\{\hat {\mathbf {y} }}&={\frac {y{\hat {\boldsymbol {\rho }}}+x{\hat {\boldsymbol {\varphi }}}}{\sqrt {x^{2}+y^{2}}}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}}$	${\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&={\frac {x\left({\sqrt {x^{2}+y^{2}}}{\hat {\mathbf {r} }}+z{\hat {\boldsymbol {\theta }}}\right)-y{\sqrt {x^{2}+y^{2}+z^{2}}}{\hat {\boldsymbol {\varphi }}}}{{\sqrt {x^{2}+y^{2}}}{\sqrt {x^{2}+y^{2}+z^{2}}}}}\\{\hat {\mathbf {y} }}&={\frac {y\left({\sqrt {x^{2}+y^{2}}}{\hat {\mathbf {r} }}+z{\hat {\boldsymbol {\theta }}}\right)+x{\sqrt {x^{2}+y^{2}+z^{2}}}{\hat {\boldsymbol {\varphi }}}}{{\sqrt {x^{2}+y^{2}}}{\sqrt {x^{2}+y^{2}+z^{2}}}}}\\{\hat {\mathbf {z} }}&={\frac {z{\hat {\mathbf {r} }}-{\sqrt {x^{2}+y^{2}}}{\hat {\boldsymbol {\theta }}}}{\sqrt {x^{2}+y^{2}+z^{2}}}}\end{aligned}}}$
Цилиндрический	${\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&=\cos \varphi {\hat {\mathbf {x} }}+\sin \varphi {\hat {\mathbf {y} }}\\{\hat {\boldsymbol {\varphi }}}&=-\sin \varphi {\hat {\mathbf {x} }}+\cos \varphi {\hat {\mathbf {y} }}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}}$	Нет данных	${\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&={\frac {\rho {\hat {\mathbf {r} }}+z{\hat {\boldsymbol {\theta }}}}{\sqrt {\rho ^{2}+z^{2}}}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&={\frac {z{\hat {\mathbf {r} }}-\rho {\hat {\boldsymbol {\theta }}}}{\sqrt {\rho ^{2}+z^{2}}}}\end{aligned}}}$
Сферический	${\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&=\sin \theta \left(\cos \varphi {\hat {\mathbf {x} }}+\sin \varphi {\hat {\mathbf {y} }}\right)+\cos \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\theta }}}&=\cos \theta \left(\cos \varphi {\hat {\mathbf {x} }}+\sin \varphi {\hat {\mathbf {y} }}\right)-\sin \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\varphi }}}&=-\sin \varphi {\hat {\mathbf {x} }}+\cos \varphi {\hat {\mathbf {y} }}\end{aligned}}}$	${\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&=\sin \theta {\hat {\boldsymbol {\rho }}}+\cos \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\theta }}}&=\cos \theta {\hat {\boldsymbol {\rho }}}-\sin \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\end{aligned}}}$	Нет данных

Формула дель

Таблица с дель оператор в декартовых, цилиндрических и сферических координатах

Операция	Декартовы координаты (Икс, у, z)	Цилиндрические координаты (ρ, φ, z)	Сферические координаты (р, θ, φ), куда φ азимутальный и θ это полярный уголα
Векторное поле А	${\displaystyle A_{x}{\hat {\mathbf {x} }}+A_{y}{\hat {\mathbf {y} }}+A_{z}{\hat {\mathbf {z} }}}$	${\displaystyle A_{\rho }{\hat {\boldsymbol {\rho }}}+A_{\varphi }{\hat {\boldsymbol {\varphi }}}+A_{z}{\hat {\mathbf {z} }}}$	${\displaystyle A_{r}{\hat {\mathbf {r} }}+A_{\theta }{\hat {\boldsymbol {\theta }}}+A_{\varphi }{\hat {\boldsymbol {\varphi }}}}$
Градиент ∇ж[1]	${\displaystyle {\partial f \over \partial x}{\hat {\mathbf {x} }}+{\partial f \over \partial y}{\hat {\mathbf {y} }}+{\partial f \over \partial z}{\hat {\mathbf {z} }}}$	${\displaystyle {\partial f \over \partial \rho }{\hat {\boldsymbol {\rho }}}+{1 \over \rho }{\partial f \over \partial \varphi }{\hat {\boldsymbol {\varphi }}}+{\partial f \over \partial z}{\hat {\mathbf {z} }}}$	${\displaystyle {\partial f \over \partial r}{\hat {\mathbf {r} }}+{1 \over r}{\partial f \over \partial \theta }{\hat {\boldsymbol {\theta }}}+{1 \over r\sin \theta }{\partial f \over \partial \varphi }{\hat {\boldsymbol {\varphi }}}}$
Расхождение ∇ ⋅ А[1]	${\displaystyle {\partial A_{x} \over \partial x}+{\partial A_{y} \over \partial y}+{\partial A_{z} \over \partial z}}$	${\displaystyle {1 \over \rho }{\partial \left(\rho A_{\rho }\right) \over \partial \rho }+{1 \over \rho }{\partial A_{\varphi } \over \partial \varphi }+{\partial A_{z} \over \partial z}}$	${\displaystyle {1 \over r^{2}}{\partial \left(r^{2}A_{r}\right) \over \partial r}+{1 \over r\sin \theta }{\partial \over \partial \theta }\left(A_{\theta }\sin \theta \right)+{1 \over r\sin \theta }{\partial A_{\varphi } \over \partial \varphi }}$
Завиток ∇ × А[1]	${\displaystyle {\begin{aligned}\left({\frac {\partial A_{z}}{\partial y}}-{\frac {\partial A_{y}}{\partial z}}\right)&{\hat {\mathbf {x} }}\\+\left({\frac {\partial A_{x}}{\partial z}}-{\frac {\partial A_{z}}{\partial x}}\right)&{\hat {\mathbf {y} }}\\+\left({\frac {\partial A_{y}}{\partial x}}-{\frac {\partial A_{x}}{\partial y}}\right)&{\hat {\mathbf {z} }}\end{aligned}}}$	${\displaystyle {\begin{aligned}\left({\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \varphi }}-{\frac {\partial A_{\varphi }}{\partial z}}\right)&{\hat {\boldsymbol {\rho }}}\\+\left({\frac {\partial A_{\rho }}{\partial z}}-{\frac {\partial A_{z}}{\partial \rho }}\right)&{\hat {\boldsymbol {\varphi }}}\\{}+{\frac {1}{\rho }}\left({\frac {\partial \left(\rho A_{\varphi }\right)}{\partial \rho }}-{\frac {\partial A_{\rho }}{\partial \varphi }}\right)&{\hat {\mathbf {z} }}\end{aligned}}}$	${\displaystyle {\begin{aligned}{\frac {1}{r\sin \theta }}\left({\frac {\partial }{\partial \theta }}\left(A_{\varphi }\sin \theta \right)-{\frac {\partial A_{\theta }}{\partial \varphi }}\right)&{\hat {\mathbf {r} }}\\{}+{\frac {1}{r}}\left({\frac {1}{\sin \theta }}{\frac {\partial A_{r}}{\partial \varphi }}-{\frac {\partial }{\partial r}}\left(rA_{\varphi }\right)\right)&{\hat {\boldsymbol {\theta }}}\\{}+{\frac {1}{r}}\left({\frac {\partial }{\partial r}}\left(rA_{\theta }\right)-{\frac {\partial A_{r}}{\partial \theta }}\right)&{\hat {\boldsymbol {\varphi }}}\end{aligned}}}$
Оператор Лапласа ∇^2ж ≡ ∆ж[1]	${\displaystyle {\partial ^{2}f \over \partial x^{2}}+{\partial ^{2}f \over \partial y^{2}}+{\partial ^{2}f \over \partial z^{2}}}$	${\displaystyle {1 \over \rho }{\partial \over \partial \rho }\left(\rho {\partial f \over \partial \rho }\right)+{1 \over \rho ^{2}}{\partial ^{2}f \over \partial \varphi ^{2}}+{\partial ^{2}f \over \partial z^{2}}}$	${\displaystyle {1 \over r^{2}}{\partial \over \partial r}\!\left(r^{2}{\partial f \over \partial r}\right)\!+\!{1 \over r^{2}\!\sin \theta }{\partial \over \partial \theta }\!\left(\sin \theta {\partial f \over \partial \theta }\right)\!+\!{1 \over r^{2}\!\sin ^{2}\theta }{\partial ^{2}f \over \partial \varphi ^{2}}}$
Векторный лапласиан ∇^2А ≡ ∆А	${\displaystyle \nabla ^{2}A_{x}{\hat {\mathbf {x} }}+\nabla ^{2}A_{y}{\hat {\mathbf {y} }}+\nabla ^{2}A_{z}{\hat {\mathbf {z} }}}$	- Просмотрите, нажав [показать] - ${\displaystyle {\begin{aligned}{\mathopen {}}\left(\nabla ^{2}A_{\rho }-{\frac {A_{\rho }}{\rho ^{2}}}-{\frac {2}{\rho ^{2}}}{\frac {\partial A_{\varphi }}{\partial \varphi }}\right){\mathclose {}}&{\hat {\boldsymbol {\rho }}}\\+{\mathopen {}}\left(\nabla ^{2}A_{\varphi }-{\frac {A_{\varphi }}{\rho ^{2}}}+{\frac {2}{\rho ^{2}}}{\frac {\partial A_{\rho }}{\partial \varphi }}\right){\mathclose {}}&{\hat {\boldsymbol {\varphi }}}\\{}+\nabla ^{2}A_{z}&{\hat {\mathbf {z} }}\end{aligned}}}$	- Просмотрите, нажав [показать] - ${\displaystyle {\begin{aligned}\left(\nabla ^{2}A_{r}-{\frac {2A_{r}}{r^{2}}}-{\frac {2}{r^{2}\sin \theta }}{\frac {\partial \left(A_{\theta }\sin \theta \right)}{\partial \theta }}-{\frac {2}{r^{2}\sin \theta }}{\frac {\partial A_{\varphi }}{\partial \varphi }}\right)&{\hat {\mathbf {r} }}\\+\left(\nabla ^{2}A_{\theta }-{\frac {A_{\theta }}{r^{2}\sin ^{2}\theta }}+{\frac {2}{r^{2}}}{\frac {\partial A_{r}}{\partial \theta }}-{\frac {2\cos \theta }{r^{2}\sin ^{2}\theta }}{\frac {\partial A_{\varphi }}{\partial \varphi }}\right)&{\hat {\boldsymbol {\theta }}}\\+\left(\nabla ^{2}A_{\varphi }-{\frac {A_{\varphi }}{r^{2}\sin ^{2}\theta }}+{\frac {2}{r^{2}\sin \theta }}{\frac {\partial A_{r}}{\partial \varphi }}+{\frac {2\cos \theta }{r^{2}\sin ^{2}\theta }}{\frac {\partial A_{\theta }}{\partial \varphi }}\right)&{\hat {\boldsymbol {\varphi }}}\end{aligned}}}$
Существенная производнаяα[2] (А ⋅ ∇)B	${\displaystyle \mathbf {A} \cdot \nabla B_{x}{\hat {\mathbf {x} }}+\mathbf {A} \cdot \nabla B_{y}{\hat {\mathbf {y} }}+\mathbf {A} \cdot \nabla B_{z}{\hat {\mathbf {z} }}}$	${\displaystyle {\begin{aligned}\left(A_{\rho }{\frac {\partial B_{\rho }}{\partial \rho }}+{\frac {A_{\varphi }}{\rho }}{\frac {\partial B_{\rho }}{\partial \varphi }}+A_{z}{\frac {\partial B_{\rho }}{\partial z}}-{\frac {A_{\varphi }B_{\varphi }}{\rho }}\right)&{\hat {\boldsymbol {\rho }}}\\+\left(A_{\rho }{\frac {\partial B_{\varphi }}{\partial \rho }}+{\frac {A_{\varphi }}{\rho }}{\frac {\partial B_{\varphi }}{\partial \varphi }}+A_{z}{\frac {\partial B_{\varphi }}{\partial z}}+{\frac {A_{\varphi }B_{\rho }}{\rho }}\right)&{\hat {\boldsymbol {\varphi }}}\\+\left(A_{\rho }{\frac {\partial B_{z}}{\partial \rho }}+{\frac {A_{\varphi }}{\rho }}{\frac {\partial B_{z}}{\partial \varphi }}+A_{z}{\frac {\partial B_{z}}{\partial z}}\right)&{\hat {\mathbf {z} }}\end{aligned}}}$	- Просмотрите, нажав [показать] - ${\displaystyle {\begin{aligned}\left(A_{r}{\frac {\partial B_{r}}{\partial r}}+{\frac {A_{\theta }}{r}}{\frac {\partial B_{r}}{\partial \theta }}+{\frac {A_{\varphi }}{r\sin \theta }}{\frac {\partial B_{r}}{\partial \varphi }}-{\frac {A_{\theta }B_{\theta }+A_{\varphi }B_{\varphi }}{r}}\right)&{\hat {\mathbf {r} }}\\+\left(A_{r}{\frac {\partial B_{\theta }}{\partial r}}+{\frac {A_{\theta }}{r}}{\frac {\partial B_{\theta }}{\partial \theta }}+{\frac {A_{\varphi }}{r\sin \theta }}{\frac {\partial B_{\theta }}{\partial \varphi }}+{\frac {A_{\theta }B_{r}}{r}}-{\frac {A_{\varphi }B_{\varphi }\cot \theta }{r}}\right)&{\hat {\boldsymbol {\theta }}}\\+\left(A_{r}{\frac {\partial B_{\varphi }}{\partial r}}+{\frac {A_{\theta }}{r}}{\frac {\partial B_{\varphi }}{\partial \theta }}+{\frac {A_{\varphi }}{r\sin \theta }}{\frac {\partial B_{\varphi }}{\partial \varphi }}+{\frac {A_{\varphi }B_{r}}{r}}+{\frac {A_{\varphi }B_{\theta }\cot \theta }{r}}\right)&{\hat {\boldsymbol {\varphi }}}\end{aligned}}}$
Тензор ∇ ⋅ Т (не путать с Тензорная дивергенция 2-го порядка )	- Просмотрите, нажав [показать] - ${\displaystyle {\begin{aligned}\left({\frac {\partial T_{xx}}{\partial x}}+{\frac {\partial T_{yx}}{\partial y}}+{\frac {\partial T_{zx}}{\partial z}}\right)&{\hat {\mathbf {x} }}\\+\left({\frac {\partial T_{xy}}{\partial x}}+{\frac {\partial T_{yy}}{\partial y}}+{\frac {\partial T_{zy}}{\partial z}}\right)&{\hat {\mathbf {y} }}\\+\left({\frac {\partial T_{xz}}{\partial x}}+{\frac {\partial T_{yz}}{\partial y}}+{\frac {\partial T_{zz}}{\partial z}}\right)&{\hat {\mathbf {z} }}\end{aligned}}}$	- Просмотрите, нажав [показать] - ${\displaystyle {\begin{aligned}\left[{\frac {\partial T_{\rho \rho }}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi \rho }}{\partial \varphi }}+{\frac {\partial T_{z\rho }}{\partial z}}+{\frac {1}{\rho }}(T_{\rho \rho }-T_{\varphi \varphi })\right]&{\hat {\boldsymbol {\rho }}}\\+\left[{\frac {\partial T_{\rho \varphi }}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi \varphi }}{\partial \varphi }}+{\frac {\partial T_{z\varphi }}{\partial z}}+{\frac {1}{\rho }}(T_{\rho \varphi }+T_{\varphi \rho })\right]&{\hat {\boldsymbol {\varphi }}}\\+\left[{\frac {\partial T_{\rho z}}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi z}}{\partial \varphi }}+{\frac {\partial T_{zz}}{\partial z}}+{\frac {T_{\rho z}}{\rho }}\right]&{\hat {\mathbf {z} }}\end{aligned}}}$	- Просмотрите, нажав [показать] - ${\displaystyle {\begin{aligned}\left[{\frac {\partial T_{rr}}{\partial r}}+2{\frac {T_{rr}}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta r}}{\partial \theta }}+{\frac {\cot \theta }{r}}T_{\theta r}+{\frac {1}{r\sin \theta }}{\frac {\partial T_{\varphi r}}{\partial \varphi }}-{\frac {1}{r}}(T_{\theta \theta }+T_{\varphi \varphi })\right]&{\hat {\mathbf {r} }}\\+\left[{\frac {\partial T_{r\theta }}{\partial r}}+2{\frac {T_{r\theta }}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta \theta }}{\partial \theta }}+{\frac {\cot \theta }{r}}T_{\theta \theta }+{\frac {1}{r\sin \theta }}{\frac {\partial T_{\varphi \theta }}{\partial \varphi }}+{\frac {T_{\theta r}}{r}}-{\frac {\cot \theta }{r}}T_{\varphi \varphi }\right]&{\hat {\boldsymbol {\theta }}}\\+\left[{\frac {\partial T_{r\varphi }}{\partial r}}+2{\frac {T_{r\varphi }}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta \varphi }}{\partial \theta }}+{\frac {1}{r\sin \theta }}{\frac {\partial T_{\varphi \varphi }}{\partial \varphi }}+{\frac {T_{\varphi r}}{r}}+{\frac {\cot \theta }{r}}(T_{\theta \varphi }+T_{\varphi \theta })\right]&{\hat {\boldsymbol {\varphi }}}\end{aligned}}}$
Дифференциальное смещение dℓ[1]	${\displaystyle dx\,{\hat {\mathbf {x} }}+dy\,{\hat {\mathbf {y} }}+dz\,{\hat {\mathbf {z} }}}$	${\displaystyle d\rho \,{\hat {\boldsymbol {\rho }}}+\rho \,d\varphi \,{\hat {\boldsymbol {\varphi }}}+dz\,{\hat {\mathbf {z} }}}$	${\displaystyle dr\,{\hat {\mathbf {r} }}+r\,d\theta \,{\hat {\boldsymbol {\theta }}}+r\,\sin \theta \,d\varphi \,{\hat {\boldsymbol {\varphi }}}}$
Дифференциальная нормальная площадь dS	${\displaystyle {\begin{aligned}dy\,dz&\,{\hat {\mathbf {x} }}\\{}+dx\,dz&\,{\hat {\mathbf {y} }}\\{}+dx\,dy&\,{\hat {\mathbf {z} }}\end{aligned}}}$	${\displaystyle {\begin{aligned}\rho \,d\varphi \,dz&\,{\hat {\boldsymbol {\rho }}}\\{}+d\rho \,dz&\,{\hat {\boldsymbol {\varphi }}}\\{}+\rho \,d\rho \,d\varphi &\,{\hat {\mathbf {z} }}\end{aligned}}}$	${\displaystyle {\begin{aligned}r^{2}\sin \theta \,d\theta \,d\varphi &\,{\hat {\mathbf {r} }}\\{}+r\sin \theta \,dr\,d\varphi &\,{\hat {\boldsymbol {\theta }}}\\{}+r\,dr\,d\theta &\,{\hat {\boldsymbol {\varphi }}}\end{aligned}}}$
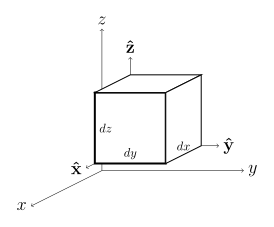
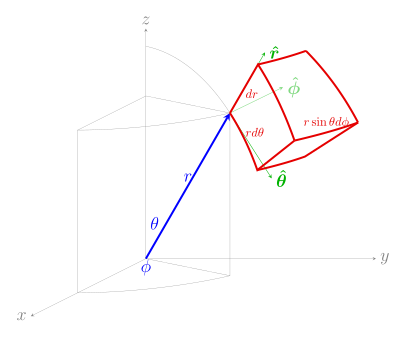
Дифференциальный объем dV[1]	${\displaystyle dx\,dy\,dz}$	${\displaystyle \rho \,d\rho \,d\varphi \,dz}$	${\displaystyle r^{2}\sin \theta \,dr\,d\theta \,d\varphi }$

^ α Эта страница использует ${\displaystyle \theta }$ для полярного угла и ${\displaystyle \varphi }$ для азимутального угла, который является общепринятым обозначением в физике. Источник, который используется для этих формул, использует ${\displaystyle \theta }$ для азимутального угла и ${\displaystyle \varphi }$ для полярного угла, который является общепринятым математическим обозначением. Чтобы получить математические формулы, переключите ${\displaystyle \theta }$ и ${\displaystyle \varphi }$ в формулах, приведенных в таблице выше.

Нетривиальные правила расчета

1. ${\displaystyle \operatorname {div} \,\operatorname {grad} f\equiv \nabla \cdot \nabla f\equiv \nabla ^{2}f}$
2. ${\displaystyle \operatorname {curl} \,\operatorname {grad} f\equiv \nabla \times \nabla f=\mathbf {0} }$
3. ${\displaystyle \operatorname {div} \,\operatorname {curl} \mathbf {A} \equiv \nabla \cdot (\nabla \times \mathbf {A} )=0}$
4. ${\displaystyle \operatorname {curl} \,\operatorname {curl} \mathbf {A} \equiv \nabla \times (\nabla \times \mathbf {A} )=\nabla (\nabla \cdot \mathbf {A} )-\nabla ^{2}\mathbf {A} }$ (Формула Лагранжа для del)
5. ${\displaystyle \nabla ^{2}(fg)=f\nabla ^{2}g+2\nabla f\cdot \nabla g+g\nabla ^{2}f}$

Декартово происхождение

${\displaystyle {\begin{aligned}\operatorname {div} \mathbf {A} =\lim _{V\to 0}{\frac {\iint _{\partial V}\mathbf {A} \cdot d\mathbf {S} }{\iiint _{V}dV}}&={\frac {A_{x}(x+dx)dydz-A_{x}(x)dydz+A_{y}(y+dy)dxdz-A_{y}(y)dxdz+A_{z}(z+dz)dxdy-A_{z}(z)dxdy}{dxdydz}}\\&={\frac {\partial A_{x}}{\partial x}}+{\frac {\partial A_{y}}{\partial y}}+{\frac {\partial A_{z}}{\partial z}}\end{aligned}}}$

${\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{x}=\lim _{S^{\perp \mathbf {\hat {x}} }\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}&={\frac {A_{z}(y+dy)dz-A_{z}(y)dz+A_{y}(z)dy-A_{y}(z+dz)dy}{dydz}}\\&={\frac {\partial A_{z}}{\partial y}}-{\frac {\partial A_{y}}{\partial z}}\end{aligned}}}$

Выражения для ${\displaystyle (\operatorname {curl} \mathbf {A} )_{y}}$ и ${\displaystyle (\operatorname {curl} \mathbf {A} )_{z}}$ находятся таким же образом.

Цилиндрическое происхождение

${\displaystyle {\begin{aligned}\operatorname {div} \mathbf {A} &=\lim _{V\to 0}{\frac {\iint _{\partial V}\mathbf {A} \cdot d\mathbf {S} }{\iiint _{V}dV}}\\&={\frac {A_{\rho }(\rho +d\rho )(\rho +d\rho )d\phi dz-A_{\rho }(\rho )\rho d\phi dz+A_{\phi }(\phi +d\phi )d\rho dz-A_{\phi }(\phi )d\rho dz+A_{z}(z+dz)d\rho (\rho +d\rho /2)d\phi -A_{z}(z)d\rho (\rho +d\rho /2)d\phi }{\rho d\phi d\rho dz}}\\&={\frac {1}{\rho }}{\frac {\partial (\rho A_{\rho })}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial A_{\phi }}{\partial \phi }}+{\frac {\partial A_{z}}{\partial z}}\end{aligned}}}$

${\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\rho }&=\lim _{S^{\perp {\boldsymbol {\hat {\rho }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}\\&={\frac {A_{\phi }(z)(\rho +d\rho )d\phi -A_{\phi }(z+dz)(\rho +d\rho )d\phi +A_{z}(\phi +d\phi )dz-A_{z}(\phi )dz}{(\rho +d\rho )d\phi dz}}\\&=-{\frac {\partial A_{\phi }}{\partial z}}+{\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \phi }}\end{aligned}}}$

${\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\phi }&=\lim _{S^{\perp {\boldsymbol {\hat {\phi }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}\\&={\frac {A_{z}(\rho )dz-A_{z}(\rho +d\rho )dz+A_{\rho }(z+dz)d\rho -A_{\rho }(z)d\rho }{d\rho dz}}\\&=-{\frac {\partial A_{z}}{\partial \rho }}+{\frac {\partial A_{\rho }}{\partial z}}\end{aligned}}}$

${\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{z}&=\lim _{S^{\perp {\boldsymbol {\hat {z}}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}\\&={\frac {A_{\rho }(\phi )d\rho -A_{\rho }(\phi +d\phi )d\rho +A_{\phi }(\rho +d\rho )(\rho +d\rho )d\phi -A_{\phi }(\rho )\rho d\phi }{\rho d\rho d\phi }}\\&=-{\frac {1}{\rho }}{\frac {\partial A_{\rho }}{\partial \phi }}+{\frac {1}{\rho }}{\frac {\partial (\rho A_{\phi })}{\partial \rho }}\end{aligned}}}$

${\displaystyle {\begin{aligned}\operatorname {curl} \mathbf {A} &=(\operatorname {curl} \mathbf {A} )_{\rho }{\hat {\boldsymbol {\rho }}}+(\operatorname {curl} \mathbf {A} )_{\phi }{\hat {\boldsymbol {\phi }}}+(\operatorname {curl} \mathbf {A} )_{z}{\hat {\boldsymbol {z}}}\\&=\left({\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \phi }}-{\frac {\partial A_{\phi }}{\partial z}}\right){\hat {\boldsymbol {\rho }}}+\left({\frac {\partial A_{\rho }}{\partial z}}-{\frac {\partial A_{z}}{\partial \rho }}\right){\hat {\boldsymbol {\phi }}}+{\frac {1}{\rho }}\left({\frac {\partial (\rho A_{\phi })}{\partial \rho }}-{\frac {\partial A_{\rho }}{\partial \phi }}\right){\hat {\boldsymbol {z}}}\end{aligned}}}$

Сферическое происхождение

${\displaystyle {\begin{aligned}\operatorname {div} \mathbf {A} &=\lim _{V\to 0}{\frac {\iint _{\partial V}\mathbf {A} \cdot d\mathbf {S} }{\iiint _{V}dV}}\\&={\frac {A_{r}(r+dr)(r+dr)d\theta \,(r+dr)\sin \theta d\phi -A_{r}(r)rd\theta \,r\sin \theta d\phi +A_{\theta }(\theta +d\theta )\sin(\theta +d\theta )\,rdrd\phi -A_{\theta }(\theta )\sin(\theta )\,rdrd\phi +A_{\phi }(\phi +d\phi )rdrd\theta -A_{\phi }(\phi )rdrd\theta }{dr\,rd\theta \,r\sin \theta d\phi }}\\&={\frac {1}{r^{2}}}{\frac {\partial (r^{2}A_{r})}{\partial r}}+{\frac {1}{r\sin \theta }}{\frac {\partial (A_{\theta }\sin \theta )}{\partial \theta }}+{\frac {1}{r\sin \theta }}{\frac {\partial A_{\phi }}{\partial \phi }}\end{aligned}}}$

${\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{r}=\lim _{S^{\perp {\boldsymbol {\hat {r}}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}&={\frac {A_{\theta }(\phi )\,rd\theta +A_{\phi }(\theta +d\theta )\,r\sin(\theta +d\theta )d\phi -A_{\theta }(\phi +d\phi )\,rd\theta -A_{\phi }(\theta )\,r\sin(\theta )d\phi }{rd\theta \,r\sin \theta d\phi }}\\&={\frac {1}{r\sin \theta }}{\frac {\partial (A_{\phi }\sin \theta )}{\partial \theta }}-{\frac {1}{r\sin \theta }}{\frac {\partial A_{\theta }}{\partial \phi }}\end{aligned}}}$

${\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\theta }=\lim _{S^{\perp {\boldsymbol {\hat {\theta }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}&={\frac {A_{\phi }(r)\,r\sin \theta d\phi +A_{r}(\phi +d\phi )dr-A_{\phi }(r+dr)(r+dr)\sin \theta d\phi -A_{r}(\phi )dr}{dr\,r\sin \theta d\phi }}\\&={\frac {1}{r\sin \theta }}{\frac {\partial A_{r}}{\partial \phi }}-{\frac {1}{r}}{\frac {\partial (rA_{\phi })}{\partial r}}\end{aligned}}}$

${\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\phi }=\lim _{S^{\perp {\boldsymbol {\hat {\phi }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}&={\frac {A_{r}(\theta )dr+A_{\theta }(r+dr)(r+dr)d\theta -A_{r}(\theta +d\theta )dr-A_{\theta }(r)\,rd\theta }{(r)drd\theta }}\\&={\frac {1}{r}}{\frac {\partial (rA_{\theta })}{\partial r}}-{\frac {1}{r}}{\frac {\partial A_{r}}{\partial \theta }}\end{aligned}}}$

${\displaystyle \operatorname {curl} \mathbf {A} =(\operatorname {curl} \mathbf {A} )_{r}\,{\hat {\boldsymbol {r}}}+(\operatorname {curl} \mathbf {A} )_{\theta }\,{\hat {\boldsymbol {\theta }}}+(\operatorname {curl} \mathbf {A} )_{\phi }\,{\hat {\boldsymbol {\phi }}}={\frac {1}{r\sin \theta }}\left({\frac {\partial (A_{\phi }\sin \theta )}{\partial \theta }}-{\frac {\partial A_{\theta }}{\partial \phi }}\right){\hat {\boldsymbol {r}}}+{\frac {1}{r}}\left({\frac {1}{\sin \theta }}{\frac {\partial A_{r}}{\partial \phi }}-{\frac {\partial (rA_{\phi })}{\partial r}}\right){\hat {\boldsymbol {\theta }}}+{\frac {1}{r}}\left({\frac {\partial (rA_{\theta })}{\partial r}}-{\frac {\partial A_{r}}{\partial \theta }}\right){\hat {\boldsymbol {\phi }}}}$

Формула преобразования единичного вектора

Единичный вектор координатного параметра ты определяется таким образом, что небольшое положительное изменение ты вызывает вектор положения ${\displaystyle {\boldsymbol {\vec {r}}}}$ изменить в ${\displaystyle {\boldsymbol {\hat {u}}}}$ направление.

Следовательно,

${\displaystyle {\partial {\boldsymbol {\vec {r}}} \over \partial u}={\partial {s} \over \partial u}{\boldsymbol {\hat {u}}}}$

куда s - параметр длины дуги.

Для двух наборов систем координат ${\displaystyle u_{i}}$ и ${\displaystyle v_{j}}$, в соответствии с Правило цепи,

${\displaystyle d{\boldsymbol {\vec {r}}}=\sum _{i}{\partial {\boldsymbol {\vec {r}}} \over \partial u_{i}}du_{i}=\sum _{i}{\partial {s} \over \partial u_{i}}{\boldsymbol {\hat {u_{i}}}}du_{i}=\sum _{j}{\partial {s} \over \partial v_{j}}{\boldsymbol {\hat {v_{j}}}}dv_{j}=\sum _{j}{\partial {s} \over \partial v_{j}}{\boldsymbol {\hat {v_{j}}}}\sum _{i}{\partial {v_{j}} \over \partial u_{i}}du_{i}=\sum _{i}\sum _{j}{\partial {s} \over \partial v_{j}}{\partial {v_{j}} \over \partial u_{i}}{\boldsymbol {\hat {v_{j}}}}du_{i}}$

Теперь мы изолируем ${\displaystyle i^{th}}$ компонент. За ${\displaystyle i{\neq }k}$, позволять ${\displaystyle du_{k}=0}$. Затем разделите с обеих сторон на ${\displaystyle du_{i}}$ получить:

${\displaystyle {\partial {s} \over \partial u_{i}}{\boldsymbol {\hat {u_{i}}}}=\sum _{j}{\partial {s} \over \partial v_{j}}{\partial {v_{j}} \over \partial u_{i}}{\boldsymbol {\hat {v_{j}}}}}$

Смотрите также

• Del
• Ортогональные координаты
• Криволинейные координаты
• Векторные поля в цилиндрических и сферических координатах

Рекомендации

1. Гриффитс, Дэвид Дж. (2012). Введение в электродинамику. Пирсон. ISBN  978-0-321-85656-2.
2. Вайсштейн, Эрик В. «Конвективный оператор». Mathworld. Получено 23 марта 2011.

внешняя ссылка

• Скрипты системы компьютерной алгебры Maxima для генерации некоторых из этих операторов в цилиндрических и сферических координатах.