Граничные условия в гидродинамике - Boundary conditions in fluid dynamics

Дальнейшая информация: Граничные условия в вычислительной гидродинамике

Граничные условия в гидродинамике набор ограничений для краевые задачи в вычислительная гидродинамика. Эти граничные условия включают в себя граничные условия на входе, граничные условия на выходе, граничные условия на стенке, граничные условия постоянного давления, осесимметричные граничные условия, симметричные граничные условия и периодические или циклические граничные условия.

Переходный Задачи требуют еще одного - начальных условий, в которых начальные значения переменных потока задаются в узлах области потока.^[1] Различные типы граничных условий используются в CFD для различных условий и целей и обсуждаются ниже.

Входные граничные условия

Отображение скорости потока на входе в трубу

В вход граничные условия, распределение всего потока переменные необходимо указывать в основном на входных границах скорость потока.^[1] Этот тип граничных условий является обычным и задается в основном там, где скорость потока на входе известна.

Граничное условие на выходе

Отображение скорости потока на выходе в трубе

В граничных условиях на выходе распределение всего потока переменные необходимо указать, в основном скорость потока. Это можно рассматривать как соединение с граничным условием на входе. Этот тип граничных условий является обычным и задается в основном там, где известна выходная скорость.^[1] Поток достигает полностью развитое государство где не происходит изменения направления потока, когда выходное отверстие выбрано вдали от геометрических возмущений. В таком регионе можно было бы выделить торговую точку и градиент всех переменных можно приравнять к нулю в направлении потока, кроме давление.

Граничное условие прилипания

Отображение граничного условия стены

Наиболее частая граница, которая встречается в ограниченный поток жидкости проблемы - это стена водовода. Соответствующее требование называется граничное условие прилипания, в котором нормальная составляющая скорости зафиксирована на нуле, а тангенциальная составляющая установлена ​​равной скорости стенки.^[1] Это может противоречить интуиции, но условие отсутствия скольжения было твердо установлено как в эксперименте, так и в теории, хотя и только после десятилетий споров и дебатов.^[2]

${\displaystyle V_{\textrm {normal}}=0}$
${\displaystyle V_{\textrm {tangential}}=V_{\textrm {wall}}}$

Теплопередача через стену можно указать или если стены считаются адиабатический, то теплопередача через стена установлен на ноль.

${\displaystyle Q_{\textrm {AdiabaticWalls}}=0}$

Граничные условия постоянного давления

Отображение граничного условия постоянного давления

Этот тип граничных условий используется, когда граничные значения давление известны, и точные детали распределения потока неизвестны. Это в основном включает условия давления на входе и выходе. Типичные примеры, в которых используется это граничное условие, включают потоки, управляемые плавучестью, внутренние потоки с несколькими выходами, потоки со свободной поверхностью и внешние потоки вокруг предметов.^[1] Пример - выход потока в атмосфера куда давление атмосферный.

Осесимметричные граничные условия

Отображение осесимметричного граничного условия

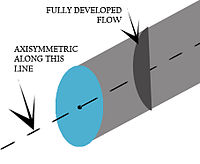
В этом граничном условии модель имеет вид осесимметричный по отношению к главной оси так, чтобы в конкретном р = р, все θs и каждый z = Z-слой, каждая переменная потока имеет одно и то же значение.^[3] Хорошим примером является поток в круглой трубе, где оси потока и трубы совпадают.

${\displaystyle V_{r}(R,\theta ,Z)=Constant}$${\displaystyle (r=R,\theta ,Z)}$

Симметричное граничное условие

Отображение симметричного граничного условия

В этом граничном условии предполагается, что по обе стороны границы существуют одинаковые физические процессы.^[4] Все переменные имеют одинаковое значение и градиенты на одинаковом расстоянии от границы. Он действует как зеркало который отражает все распределение потока на другую сторону.^[5]Условия на симметричной границе отсутствуют. поток через границу и без скаляра поток через границу.

Хороший пример - поток в трубе с симметричный препятствие в потоке. Препятствие разделяет верхний поток и нижний поток как зеркальный поток.

Периодическое или циклическое граничное условие

Четверть, показывающая циклическое граничное условие

А периодический или же циклический граничное условие возникает из другого типа симметрия в проблеме. Если компонент имеет повторяющуюся картину распределения потока более двух раз, что нарушает требования к зеркальному отображению, необходимые для симметричного граничного условия. Хорошим примером может служить лопастной насос (рис.),^[6] где отмеченная область повторяется четыре раза в координатах r-тета. Циклически-симметричные области должны иметь одинаковые переменные потока и распределение и должны удовлетворять этим требованиям в каждом Z-слое.^[1]

Смотрите также

• Кондиционирование потока
• Проблема начального значения

Примечания

1. Хенк Карле Верстеег; Weeratunge Malalasekera (1995). Введение в вычислительную гидродинамику: метод конечных объемов. Longman Scientific & Technical. С. 192–206. ISBN  0-582-21884-5.
2. Прабхакара, Сандип; Дешпанде, М. Д. (2004-04-01). «Граничное условие прилипания в механике жидкости». Резонанс. 9 (4): 50–60. Дои:10.1007 / BF02834856. ISSN  0973-712X. S2CID  124269972.
3. "циклические симметричные БК". Получено 2015-08-09.
4. "циклические симметричные БК". Получено 2013-10-10.
5. «Симметричное граничное условие».
6. "циклические симметричные БК". Получено 2013-10-10.

Рекомендации

• Верстег (1995). «Глава 9». Введение в вычислительную гидродинамику Метод конечных объемов, 2 / e. Longman Scientific & Technical. С. 192–206. ISBN  0-582-21884-5.
• «Симметричное граничное условие».
• "циклические симметричные БК". Получено 2013-10-10.