Blanuša Snarks - Blanuša snarks

Blanuša Snarks
Первый снарк Blanuša
Названный в честь	Данило Блануша
Вершины	18 (оба)
Края	27 (оба)
Радиус	4 (оба)
Диаметр	4 (оба)
Обхват	5 (оба)
Автоморфизмы	8, D4 (1-й) 4, Кляйн группа (2-й)
Хроматическое число	3 (оба)
Хроматический индекс	4 (оба)
Толщина книги	3 (оба)
Номер очереди	2 (оба)
Характеристики	Снарк (обе) Гипогамильтониан (обе) Кубический (обе) Тороидальный (только один)[1]
Таблица графиков и параметров

в математический поле теория графов, то Blanuša Snarks два 3-регулярные графики с 18 вершинами и 27 ребрами.^[2] Они были обнаружены Югославский математик Данило Блануша в 1946 году и названы его именем.^[3] При обнаружении был известен только один снарк - Граф Петерсена.

В качестве язвы, Снарки Блануши связаны, без мостов кубические графы с хроматический индекс равно 4. У обоих есть хроматическое число 3, диаметр 4 и обхват 5. Они негамильтониан но есть гипогамильтониан.^[4] Как есть толщина книги 3 и номер очереди 2.^[5]

Алгебраические свойства

В группа автоморфизмов первого снарка Blanuša имеет порядок 8 и изоморфный к Группа диэдра D₄, группа симметрий квадрата.

Группа автоморфизмов второго снарка Блануши является абелева группа порядка 4, изоморфного Кляйн четыре группы, то прямой продукт из Циклическая группа Z/2Z с собой.

В характеристический многочлен первого и второго снарка Blanuša соответственно:

${\displaystyle (x-3)(x-1)^{3}(x+1)(x+2)(x^{4}+x^{3}-7x^{2}-5x+6)(x^{4}+x^{3}-5x^{2}-3x+4)^{2}\ }$

${\displaystyle (x-3)(x-1)^{3}(x^{3}+2x^{2}-3x-5)(x^{3}+2x^{2}-x-1)(x^{4}+x^{3}-7x^{2}-6x+7)(x^{4}+x^{3}-5x^{2}-4x+3).\ }$

Обобщенные снарки Блануши

Существует обобщение первого и второго снарков Блануши на два бесконечных семейства снарков 8-го порядка.п+10 обозначено ${\displaystyle B_{n}^{1}}$ и ${\displaystyle B_{n}^{2}}$. Снарки Блануши - самые маленькие члены этих двух бесконечных семейств.^[6]

В 2007 г. Я. Мазак доказал, что круговой хроматический индекс 1-го типа обобщает снарки Блануши. ${\displaystyle B_{n}^{1}}$ равно ${\displaystyle 3+{\frac {2}{n}}}$.^[7]

В 2008 г. М. Гебле доказал, что круговой хроматический индекс 2-го типа обобщает снарки Блануши. ${\displaystyle B_{n}^{2}}$ равно ${\displaystyle 3+{\frac {1}{\lfloor 1+3n/2\rfloor }}}$.^[8]

Галерея

• 

  В хроматическое число первого снарка Blanuša - 3.

• 

  В хроматический индекс первого снарка Blanuša - 4.

• 

  В хроматическое число второго снарка Blanuša - 3.

• 

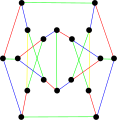
  В хроматический индекс второго снарка Blanuša - 4.

Рекомендации

1. Орбанич, Ален; Писанский, Томаж; Рандич, Милан; Серватиус, Бриджит (2004). "Блануша дабл". Математика. Commun. 9 (1): 91–103.
2. Вайсштейн, Эрик В. "Блануша снаркс". MathWorld.
3. Блануша, Д., "Проблема cetiriju boja." Гласник Мат. Физ. Astr. Сер. II. 1, 31-42, 1946.
4. Экхард Стин, «О бикритических снарках», Math. Словака, 1997.
5. Вольц, Джессика; Инженерные линейные схемы с SAT. Магистерская работа, Тюбингенский университет, 2018 г.
6. Рид Р. К. и Уилсон Р. Дж. Атлас графиков. Оксфорд, Англия: Издательство Оксфордского университета, стр. 276 и 280, 1998.
7. Й. Мазак, Круговой хроматический индекс снарков, магистерская диссертация, Университет Коменского в Братиславе, 2007.
8. М. Гебле, Круговой хроматический индекс обобщенных снарков Блануши, Электронный журнал комбинаторики, том 15, 2008.