Многогранник Силасси - Szilassi polyhedron
| Многогранник Силасси | |
|---|---|
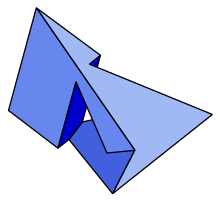 | |
| Тип | Тороидальный многогранник |
| Лица | 7 шестиугольники |
| Края | 21 |
| Вершины | 14 |
| χ | 0 (род 1) |
| Конфигурация вершины | 6.6.6 |
| Группа симметрии | C1, [ ]+, (11) |
| Двойной многогранник | Многогранник Часара |
| Характеристики | Невыпуклый |
В Многогранник Силасси невыпуклый многогранник, топологически a тор, с семью шестиугольник лица.

Расцветка и симметрия
Каждая грань этого многогранника имеет одно ребро друг с другом. В результате для окраски всех смежных граней требуется семь цветов, что обеспечивает нижнюю границу для теорема семи цветов. Имеет ось симметрии 180 градусов; три пары граней конгруэнтны, оставляя один непарный шестиугольник, который имеет ту же симметрию вращения, что и многогранник. 14 вершин и 21 ребро многогранника Силасси образуют вложение График Хивуда на поверхность тора.
Полное прилегание лица

В тетраэдр и многогранник Силасси - единственные два известных многогранника, в которых каждая грань имеет общее ребро с другой гранью.
Если многогранник с ж грани встроены в поверхность с час отверстия таким образом, что каждая грань имеет общий край с другой гранью, это следует путем некоторой манипуляции с Эйлерова характеристика который
Это уравнение выполняется для тетраэдра с час = 0 и ж = 4, а для многогранника Силасси с час = 1 и ж = 7.
Следующее возможное решение, час = 6 и ж = 12, соответствует многограннику с 44 вершинами и 66 ребрами. Однако неизвестно, может ли такой многогранник быть реализован геометрически (а не в виде абстрактный многогранник ). В более общем смысле это уравнение может быть удовлетворено именно тогда, когда ж сравнимо с 0, 3, 4 или 7 по модулю 12.
История
Многогранник Силасси назван в честь венгерского математика. Лайош Сзиласси, который открыл его в 1977 году. двойной многограннику Силасси Многогранник Часара, ранее был обнаружен Акос Часар (1949 ); у него семь вершин, 21 ребро, соединяющее каждую пару вершин, и 14 треугольных граней. Как и многогранник Силасси, многогранник Часара имеет топологию тора.
| Нерешенная проблема в математике: Существует ли невыпуклый многогранник с более чем семью гранями, каждая из которых имеет ребро друг с другом? (больше нерешенных задач по математике) |
Рекомендации
- Часар, Акош (1949), «Многогранник без диагоналей», Acta Sci. Математика. Сегед, 13: 140–142.
- Гарднер, Мартин (1978), «В которой математическая эстетика применяется к современному минимальному искусству», «Математические игры», Scientific American, 239 (5): 22–32, Дои:10.1038 / Scientificamerican1178-22.
- Юнгерман, М .; Рингель, Герхард (1980), "Минимальные триангуляции на ориентируемых поверхностях", Acta Mathematica, 145 (1–2): 121–154, Дои:10.1007 / BF02414187.
- Петерсон, Иварс (2007), «Многогранник с дырой», MathTrek, Математическая ассоциация Америки.[мертвая ссылка ]
- Силасси, Лайош (1986), «Штатные тороиды» (PDF), Структурная топология, 13: 69–80
- ^ Бранко Грюнбаум, Лайош Силасси, Геометрические реализации специальных тороидальных комплексов.[мертвая ссылка ], Вклад в дискретную математику, Том 4, номер 1, страницы 21-39, ISSN 1715-0868
внешняя ссылка
- Эйс, Том, Многогранник Силасси.
- Вайсштейн, Эрик В. "Многогранник Силасси". MathWorld.
- Многогранник Силасси - Модель Papercraft в CutOutFoldUp.com

