Нить опоясывающая Землю - String girdling Earth

Визуализация, показывающая, что длина, добавленная к окружности (синий), зависит только от дополнительного радиуса (красный), а не от исходной окружности (серый)

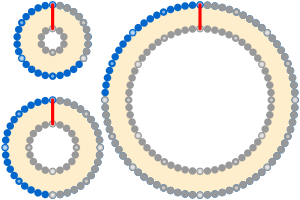
Нити опоясывающие землю математическая головоломка с нелогичный решение. В обычной версии этой головоломки веревка оборачивается вокруг экватора идеально сферической Земли. Эта струна разрезается и добавляется кусок длиной 1 метр (3 фута 3 дюйма). Теперь струна переставлена ​​так, чтобы она находилась на одинаковой высоте над экватором. Тогда возникает вопрос, позволит ли промежуток между струной и Землей проехать машине, кошке или тонкому лезвию ножа.

Решение

Учитывая, что 1 метр (3 фута 3 дюйма) почти ничтожен по сравнению с окружностью 40000 км (25000 миль), первым ответом будет то, что новое положение струны не будет отличаться от исходного положения прилегания к поверхности. Удивительно, но ответ таков: кошка легко пройдет через щель, размер которой будет 1/2π метров или около 16 см (6,3 дюйма). Еще более удивительно то, что размер сферы или круга, вокруг которого натянута струна, не имеет значения и может быть любым, от размера атома до размера Млечный Путь - результат останется около 16 см (6,3 дюйма).^[1]

Фотография, показывающая смещение между стартовыми линиями легкой атлетики

Позволять C быть окружностью Земли, р быть его радиусом, c быть добавленной длиной строки и р быть добавленным радиусом. Как круг радиуса р  имеет окружность 2πр ,

${\displaystyle {\begin{aligned}\\C+c&=2\pi (R+r)\\2\pi R+c&=2\pi R+2\pi r\\c&=2\pi r\\\therefore \;r&={\frac {c}{2\pi }}\end{aligned}}}$

независимо от стоимости C .

Следствием этого является то, что для того, чтобы поднять исходную струну на 16 см (6,3 дюйма) от земли на всем протяжении вокруг экватора, нужно добавить всего около 1 метра (3 фута 3 дюйма).

Это также означает, что на легкой атлетике смещение между стартовыми линиями на каждой дорожке одинаковое, равное 2.π умноженной на ширину полосы движения, независимо от того, составляет ли окружность стадиона стандартные 400 м (1300 футов) или размер Млечного Пути.

Смотрите также

• Визуальный расчет, интуитивно понятный способ решения проблемы этого типа, первоначально применяемый для поиска области кольцо, учитывая только его аккорд длина
• Проблема с кольцом для салфеток, еще одна проблема, когда радиус сферы не имеет значения, как это ни парадоксально.

Рекомендации

1. Ньюман, Джеймс Рой (2000). Мир математики, Том 4. Courier Dover Publications. п. 2436. ISBN  0-486-41152-4., п. 2436