Баланс оболочки - Shell balance

В механика жидкости, а баланс оболочки можно использовать для определения степени текучести скорость изменения по потоку.

Оболочка - это дифференциальный элемент потока. Глядя на импульс и силы на одной небольшой части, можно интегрировать по потоку, чтобы увидеть большую картину потока в целом. Баланс определяет, что входит в скорлупу и выходит из нее. Импульс создается внутри оболочки за счет поступления и выхода жидкости из оболочки, а также напряжение сдвига. Кроме того, есть давление и гравитационный силы на оболочке. Целью баланса оболочки является определение профиля скорости потока. Профиль скорости - это уравнение для расчета скорости на основе определенного места в потоке. Отсюда можно найти скорость для любой точки потока.

Приложения

Весы Shell можно использовать во многих ситуациях. Например, поток в трубе, поток нескольких жидкостей друг вокруг друга или поток из-за разницы давлений. Хотя условия баланса оболочки и граничные условия изменятся, базовая установка и процесс останутся прежними.

Требования к расчетам баланса Shell

В жидкости должны присутствовать:

• Ламинарный поток
• Никаких изгибов или кривых
• Устойчивое состояние
• Два граничных условия

Граничные условия используются для нахождения постоянных интегрирования.

• Жидкость - Твердый Граница: Условие без скольжения, скорость жидкости в твердом теле равна скорости твердого тела.
• Жидкость - Газ Граница: Напряжение сдвига = 0.
• Жидкость - Граница жидкости: равно скорость и напряжение сдвига на обеих жидкостях.

Выполнение балансировки оболочки

Жидкость течет между двумя горизонтальными поверхностями контактной площадки A и контактирует с ними. Используется дифференциальная оболочка высотой Δy (см. Диаграмму ниже).

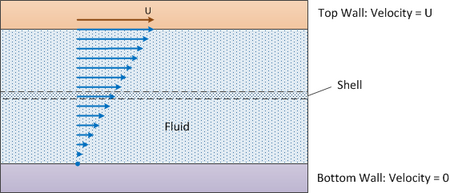
Верхняя поверхность движется со скоростью U, а нижняя поверхность неподвижна.

• Плотность жидкости = ρ
• Вязкость жидкости = μ
• Скорость в направлении x = ${\displaystyle V_{x}}$, показанный диагональной линией выше. Это то, для чего нужен баланс оболочки.

Сохранение импульса ключ к балансу Shell

• (Скорость импульс in) - (скорость выхода) + (сумма всех сил) = 0

Чтобы выполнить балансировку скорлупы, выполните следующие основные шаги:

1. Найдите импульс от напряжения сдвига (момент от напряжения сдвига в системе) - (импульс от напряжения сдвига вне системы). Импульс от напряжения сдвига входит в оболочку при у и покидает систему в у + Δу. Напряжение сдвига = τ_yx, площадь = А, импульс = τ_yxА.
2. Найдите импульс потока. Импульс вливается в систему при Икс = 0 и на Икс = L. Поток установившийся. Следовательно, поток импульса при Икс = 0 равен моменту потока при Икс = L. Следовательно, они отменяются.
3. Находить сила тяжести сила на оболочке.
4. Находить давление силы.
5. Включите режим сохранения импульса и решите τ_yx.
6. Примените закон вязкости Ньютона для Ньютоновская жидкостьτ_yx = -μ(dV_Икс/dy).
7. Выполните интеграцию, чтобы найти уравнение для скорости, и используйте граничные условия, чтобы найти константы интегрирования.

Граница 1: верхняя поверхность: y = 0 и V_Икс = U

Граница 2: Нижняя поверхность: y = D и V_Икс = 0

Примеры выполнения балансировки оболочки можно найти на перечисленных ниже ресурсах.

Ресурсы

• «Решение проблем в явлениях переноса: проблемы механики жидкости». Получено 2007-10-06.

• Харриотт, Питер; У. МакКейб; Дж. Смит (2004). Единичные операции химического машиностроения: седьмое издание. McGraw-Hill Professional. С. 68–132. ISBN  9780072848236.