Вращательно-колебательная связь - Rotational–vibrational coupling
| Связь в науке |
|---|
| Классическая муфта |
| Квантовая связь |

Вращательно-колебательная связь происходит, когда вращение частота объекта близка к естественной внутренней частоте вибрации или идентична ей. Анимация справа показывает простой пример. Движение, изображенное на анимации, предназначено для идеализированной ситуации, когда сила, проявляемая весна линейно увеличивается с расстоянием до центра вращения. Также анимация показывает, что произошло бы, если бы не было никаких трение.
При вращательно-колебательной связи возникает колебание угловая скорость. При притяжении вращающихся масс ближе к центру вращения сила пружины (a центростремительная сила ) делается работай, преобразование сохраненных энергия деформации весной в кинетическая энергия масс. Вследствие этого увеличивается угловая скорость. Сила пружины не может тянуть вращающиеся массы полностью к центру, поскольку по мере того, как вращающиеся массы перемещаются ближе к центру вращения, сила пружины ослабевает, а скорость постоянно увеличивается. В какой-то момент скорость возросла настолько, что объект снова начал раскачиваться, снова вступая в фазу накопления энергии деформации.
В вертолет должны быть предусмотрены конструкции демпфирующих устройств, потому что при определенных угловых скоростях колебания лопастей ротора могут усиливаться вращательно-колебательной связью и нарастать катастрофически. Без демпфирования колебания будут вызывать вырывание лопастей винта.
Преобразование энергии


Анимация справа дает более четкое представление о колебаниях угловой скорости. Есть близкая аналогия с гармоническое колебание.
Когда гармоническое колебание находится в своей средней точке, вся энергия системы равна кинетическая энергия. Когда гармоническое колебание происходит в точках, наиболее удаленных от средней точки, вся энергия системы равна потенциальная энергия. Энергия системы колеблется между кинетической и потенциальной энергией.
В анимации с двумя кружащимися массами есть колебания кинетической и потенциальной энергии вперед и назад. Когда пружина находится в максимальном растяжении, тогда потенциальная энергия максимальна, когда угловая скорость максимальна, кинетическая энергия максимальна.
Настоящая пружина связана с трением. С настоящей пружиной вибрация будет гашена, и в конечном итоге массы будут вращаться друг вокруг друга на постоянном расстоянии с постоянным натяжением пружины.
Математический вывод
В этом обсуждении используются следующие упрощения: сама пружина считается невесомой, а пружина считается совершенной пружиной; возвращающая сила увеличивается линейно по мере растяжения пружины. То есть возвращающая сила точно пропорциональна расстоянию до центра вращения. Возвратная сила с этой характеристикой называется гармоническая сила.
Следующее параметрическое уравнение положения как функции времени описывает движение вращающихся масс:
- (1)
- (2)
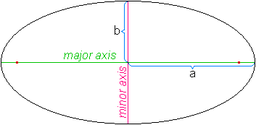
- Обозначение:
- составляет половину длины большой оси
- составляет половину длины малой оси
- составляет 360 °, разделенное на продолжительность одного оборота
Движение как функцию времени также можно рассматривать как комбинацию векторов двух равномерных круговых движений. Параметрические уравнения (1) и (2) можно переписать как:

Преобразование в систему координат, которая вычитает общее круговое движение, оставляет эксцентриситет эллиптической траектории. центр эксцентриситета находится на расстоянии от главного центра:
Фактически это то, что видно во второй анимации, в которой движение отображается в систему координат, которая вращается с постоянной угловой скоростью. Угловая скорость движения относительно вращающейся системы координат равна 2ω, что в два раза больше угловой скорости всего движения. Пружина непрерывно работает. Точнее, пружина колеблется между выполнением положительной работы (увеличение кинетической энергии груза) и выполнением отрицательной работы (уменьшение кинетической энергии груза).
Обсуждение с использованием векторной записи
Центростремительная сила - это гармоническая сила.
Множество всех решений приведенного выше уравнения движения состоит как из круговых траекторий, так и из траекторий эллиптической формы. Все решения имеют одинаковый период обращения. Это отличительная особенность движения под действием гармонической силы; для всех траекторий требуется одинаковое количество времени, чтобы совершить оборот.
Когда используется вращающаяся система координат, к уравнению движения добавляются центробежный член и член Кориолиса. Следующее уравнение дает ускорение относительно вращающейся системы объекта, движущегося по инерции.
Здесь, Ω - угловая скорость вращающейся системы координат относительно инерциальной системы координат. v - скорость движущегося объекта относительно вращающейся системы координат. Важно отметить, что центробежный член определяется угловой скоростью вращающейся системы координат; термин центробежный не имеет отношения к движению объекта.
В целом, это дает следующие три члена в уравнении движения для движения относительно системы координат, вращающейся с угловой скоростью Ω.
И центростремительная сила, и центробежный член в уравнении движения пропорциональны р. Угловая скорость вращающейся системы координат регулируется так, чтобы иметь тот же период вращения, что и объект, движущийся по траектории в форме эллипса. Следовательно, вектор центростремительной силы и вектор центробежного члена на каждом расстоянии от центра равны друг другу по величине и противоположны по направлению, поэтому эти два члена падают друг против друга.
Только в очень особых обстоятельствах вектор центростремительной силы и центробежный член падают друг против друга на каждом расстоянии до центра вращения. Это так, если и только если центростремительная сила является гармонической силой.
В этом случае в уравнении движения остается только член Кориолиса.
Поскольку вектор члена Кориолиса всегда направлен перпендикулярно скорости относительно вращающейся системы координат, из этого следует, что в случае возвращающей силы, которая является гармонической силой, эксцентриситет траектории будет проявляться как небольшое круговое движение относительно вращающейся системы координат. Коэффициент 2 члена Кориолиса соответствует периоду вращения, который составляет половину периода общего движения.
Как и ожидалось, анализ с использованием векторной записи приводит к прямому подтверждению предыдущего анализа:
Пружина непрерывно работает. Точнее, пружина колеблется между выполнением положительной работы (увеличение кинетической энергии гири) и выполнением отрицательной работы (уменьшение кинетической энергии гири).
Сохранение углового момента
В разделе «Преобразования энергии при вращательно-колебательном взаимодействии» за динамикой следует отслеживание преобразований энергии. В учебниках часто указывается, что увеличение угловой скорости при сжатии происходит в соответствии с принципом сохранение углового момента. Поскольку нет крутящий момент действуя на вращающиеся грузы, угловой момент сохраняется. Однако при этом не учитывается причинный механизм, которым является сила растянутой пружины, и работа, выполняемая во время ее сжатия и растяжения. Аналогично, когда пушка стреляет, снаряд вылетает из ствола в сторону цели, а ствол будет отдаляться, в соответствии с принципом сохранения импульс. Это не значит, что снаряд покидает ствол с большой скоростью. потому что ствол отдаляется. При этом должна происходить отдача ствола, как описано Третий закон Ньютона, это не причинный агент.
Причинный механизм заключается в преобразовании энергии: взрыв пороха преобразует потенциальную химическую энергию в потенциальную энергию сильно сжатого газа. Когда газ расширяется, его высокое давление оказывает давление как на снаряд, так и на внутреннюю часть ствола. Именно под действием этой силы потенциальная энергия преобразуется в кинетическую энергию снаряда и ствола.
В случае вращательно-колебательного сцепления причиной является сила, действующая со стороны пружины. Пружина колеблется между работой и отрицательной работой. (Работа считается отрицательной, если направление силы противоположно направлению движения.)
Смотрите также
Вращательно-колебательная спектроскопия
Рекомендации
Эта статья не цитировать любой источники. (Май 2008 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |














