Приоритетная очередь - Priority queue

В Информатика, а приоритетная очередь является абстрактный тип данных похож на обычный очередь или же куча структура данных, в которой каждый элемент дополнительно имеет связанный с ним "приоритет". В очереди с приоритетом элемент с высоким приоритетом обслуживается перед элементом с низким приоритетом. В некоторых реализациях, если два элемента имеют одинаковый приоритет, они обслуживаются в соответствии с порядком, в котором они были поставлены в очередь, тогда как в других реализациях порядок элементов с одинаковым приоритетом не определен.

Хотя приоритетные очереди часто реализуются с кучи, они концептуально отличаются от куч. Очередь с приоритетом - это такое понятие, как "a список "или" карта "; так же, как список может быть реализован с связанный список или множество, очередь приоритетов может быть реализована с помощью кучи или множества других методов, таких как неупорядоченный массив.

Операции

Очередь с приоритетом должна как минимум поддерживать следующие операции:

  • пусто: проверить, нет ли в очереди элементов.
  • insert_with_priority: добавить элемент к очередь со связанным приоритетом.
  • pull_highest_priority_element: удалить элемент из очереди, имеющий высший приоритет, и верните его.
    Это также известно как "pop_element (Выкл.)", "get_maximum_element" или же "get_front (большинство) _element".
    Некоторые соглашения меняют порядок приоритетов, считая более низкие значения более высоким приоритетом, поэтому это также может быть известно как "get_minimum_element", и часто упоминается как"получить-мин" в литературе.
    Вместо этого это может быть указано как отдельный "peek_at_highest_priority_element" и "delete_element«функции, которые можно комбинировать для производства»pull_highest_priority_element".

Кроме того, заглядывать (в этом контексте часто называют find-max или же find-min), который возвращает элемент с наивысшим приоритетом, но не изменяет очередь, очень часто реализуется и почти всегда выполняется в О(1) время. Эта операция и ее О(1) производительность имеет решающее значение для многих приложений с приоритетными очередями.

Более продвинутые реализации могут поддерживать более сложные операции, такие как pull_lowest_priority_element, проверка первых нескольких элементов с наивысшим или самым низким приоритетом, очистка очереди, очистка подмножеств очереди, выполнение пакетной вставки, объединение двух или более очередей в одну, увеличение приоритета любого элемента и т. д.

Можно представить приоритетную очередь как модифицированную очередь, но когда следующий элемент будет удален из очереди, первым будет извлечен элемент с наивысшим приоритетом.

Стеки и очереди могут быть смоделированы как отдельные виды приоритетных очередей. Напоминаем, что вот как ведут себя стеки и очереди:

В стеке приоритет каждого вставленного элемента монотонно увеличивается; таким образом, последний вставленный элемент всегда извлекается первым. В очереди приоритет каждого вставленного элемента монотонно уменьшается; таким образом, первый вставленный элемент всегда извлекается первым.

Выполнение

Наивные реализации

Существует множество простых, обычно неэффективных способов реализации очереди с приоритетами. Они предоставляют аналогию, чтобы помочь понять, что такое приоритетная очередь.

Например, можно сохранить все элементы в несортированном списке ( О(1) время вставки). Всякий раз, когда запрашивается элемент с наивысшим приоритетом, ищите среди всех элементов элемент с наивысшим приоритетом. (О(п) время тянуть),

вставлять(узел) {list.append (узел)}
тянуть() {каждый узел в списке {если высший.приоритет <узел.приорити {высший = узел}} list.remove (высший) возвращает наивысший}

В другом случае можно оставить все элементы в списке сортировки по приоритету (О(n) время сортировки вставки), всякий раз, когда запрашивается элемент с наивысшим приоритетом, может быть возвращен первый элемент в списке. ( О(1) время вытягивания)

вставлять(узел) {foreach (индекс, элемент) в списке {if node.priority 
тянуть() {высший = list.get_at_index (list.length-1) list.remove (высший) возврат наибольший}
Обычная реализация
Для повышения производительности приоритетные очереди обычно используют куча как их основу, давая О(бревно п) производительность для вставок и удалений, и О(п) для первоначальной сборки из набора п элементы. Варианты базовой структуры данных кучи, такие как спаривание кучи или же Куча Фибоначчи может дать лучшие оценки для некоторых операций.[1]
В качестве альтернативы, когда самобалансирующееся двоичное дерево поиска используется, вставка и удаление также занимают О(бревно п) времени, хотя построение деревьев из существующих последовательностей элементов занимает О(п бревно п) время; это типично, когда у кого-то уже может быть доступ к этим структурам данных, например, со сторонними или стандартными библиотеками.
С точки зрения вычислительной сложности очереди с приоритетами соответствуют алгоритмам сортировки. Раздел о эквивалентность приоритетных очередей и алгоритмов сортировки Ниже описывается, как эффективные алгоритмы сортировки могут создавать эффективные очереди с приоритетами.
Специализированные отвалы
Есть несколько специализированных куча структуры данных которые либо предоставляют дополнительные операции, либо превосходят реализации на основе кучи для определенных типов ключей, в частности, для целочисленных ключей. Предположим, что набор возможных ключей равен {1, 2, ..., C}.
  • Когда только вставлять, find-min и экстракт мин необходимы, а в случае целочисленных приоритетов очередь ведра может быть построен как массив C связанные списки плюс указатель верх, первоначально C. Вставка предмета с ключом k добавляет элемент в k'th, и обновления вверх ← min (вверху, k), как в постоянное время. Экстракт мин удаляет и возвращает один элемент из списка с индексом верх, затем увеличивает верх при необходимости, пока он снова не укажет на непустой список; это занимает О(C) время в худшем случае. Эти очереди полезны для сортировки вершин графа по их степени.[2]:374
  • А дерево ван Эмде Боас поддерживает минимум, максимум, вставлять, Удалить, поиск, экстракт мин, экстракт-макс, предшественник и преемник операции в О(журнал журнала C) времени, но занимает место для небольших очередей около О(2м/2), куда м - количество бит в значении приоритета.[3] Пространство можно значительно уменьшить с помощью хеширования.
  • В Дерево слияния к Фредман и Уиллард реализует минимум операция в О(1) время и вставлять и экстракт мин операции в время. Однако автор заявляет, что «Наши алгоритмы представляют только теоретический интерес; постоянные факторы, влияющие на время выполнения, исключают практичность».[4]
Для приложений, которые делают много "заглядывать "операций для каждой операции" extract-min ", временная сложность действий просмотра может быть уменьшена до О(1) во всех реализациях дерева и кучи путем кэширования элемента с наивысшим приоритетом после каждой вставки и удаления. Для вставки это добавляет максимум постоянную стоимость, поскольку вновь вставленный элемент сравнивается только с ранее кэшированным минимальным элементом. Для удаления это не более чем добавляет дополнительные затраты на «просмотр», которые обычно дешевле, чем затраты на удаление, поэтому общая временная сложность существенно не изменяется.
Очереди с монотонным приоритетом представляют собой специализированные очереди, оптимизированные для случая, когда никогда не вставляется элемент с более низким приоритетом (в случае min-heap), чем любой ранее извлеченный элемент. Это ограничение встречается в нескольких практических приложениях приоритетных очередей.
Сводка времени работы
Вот временные сложности[5] различных структур данных кучи. Имена функций предполагают минимальную кучу. Для значения "О(ж)" и "Θ(ж)" видеть Обозначение Big O.
Операцияfind-mindelete-minвставлятьклавиша уменьшенияобъединить
Двоичный[5]Θ(1)Θ(бревноп)О(бревноп)О(бревноп)Θ(п)
ЛевыйΘ(1)Θ(бревно п)Θ(бревно п)О(бревно п)Θ(бревно п)
Биномиальный[5][6]Θ(1)Θ(бревно п)Θ(1)[а]Θ(бревно п)О(бревноп)[b]
Фибоначчи[5][7]Θ(1)О(бревноп)[а]Θ(1)Θ(1)[а]Θ(1)
Сопряжение[8]Θ(1)О(бревно п)[а]Θ(1)о(бревноп)[а][c]Θ(1)
Brodal[11][d]Θ(1)О(бревноп)Θ(1)Θ(1)Θ(1)
Ранговые пары[13]Θ(1)О(бревно п)[а]Θ(1)Θ(1)[а]Θ(1)
Строгий Фибоначчи[14]Θ(1)О(бревно п)Θ(1)Θ(1)Θ(1)
2–3 кучи[15]О(бревно п)О(бревно п)[а]О(бревно п)[а]Θ(1)?
  1. ^ а б c d е ж грамм час я Амортизированное время.
  2. ^ п размер большей кучи.
  3. ^ Нижняя граница [9] верхняя граница [10]
  4. ^ Бродал и Окасаки позже описывают настойчивый вариант с теми же границами, за исключением клавиши уменьшения, которая не поддерживается. п элементы могут быть построены снизу вверх в О(п).[12]
Эквивалентность приоритетных очередей и алгоритмов сортировки












Использование очереди приоритетов для сортировки
В семантика о приоритетных очередях естественно предлагают метод сортировки: вставить все элементы для сортировки в приоритетную очередь и последовательно удалить их; они появятся в отсортированном порядке. На самом деле это процедура, используемая несколькими алгоритмы сортировки, однажды слой абстракция предоставленная приоритетной очередью удаляется. Этот метод сортировки эквивалентен следующим алгоритмам сортировки:
ИмяРеализация приоритетной очередиЛучшийСреднийНаихудший
HeapsortКуча
SmoothsortЛеонардо Хип
Выборочная сортировкаНеупорядоченный Множество
Вставка сортировкиУпорядоченный Множество
Сортировка дереваСамобалансирующееся двоичное дерево поиска
Использование алгоритма сортировки для создания очереди с приоритетом
Алгоритм сортировки также может использоваться для реализации очереди приоритетов. В частности, Торуп говорит:[16]
Мы представляем общее детерминированное линейное сокращение пространства от приоритетных очередей до сортировки, подразумевая, что если мы можем отсортировать до п ключи в S(п) времени на ключ, то есть очередь с приоритетом, поддерживающая Удалить и вставлять в О(S(п)) время и find-min в постоянное время.
То есть, если есть алгоритм сортировки, который может сортировать в О(S) время на ключ, где S какая-то функция п и размер слова,[17] тогда можно использовать данную процедуру для создания очереди с приоритетом, в которой вытягивание элемента с наивысшим приоритетом О(1) время, и вставка новых элементов (и удаление элементов) выполняется О(S) время. Например, если у кого-то есть О(п бревноп) алгоритм сортировки, можно создать приоритетную очередь с О(1) вытягивание и О(n журналп) вставка.
Библиотеки












Очередь с приоритетом часто считается "структура данных контейнера ".
В Стандартная библиотека шаблонов (STL), а C ++ Стандарт 1998 г., определяет priority_queue как один из STL контейнер адаптер шаблоны классов. Однако он не указывает, как должны обслуживаться два элемента с одинаковым приоритетом, и действительно, общие реализации не будут возвращать их в соответствии с их порядком в очереди. Он реализует очередь с максимальным приоритетом и имеет три параметра: объект сравнения для сортировки, такой как объект функции (по умолчанию less , если не указано), базовый контейнер для хранения структур данных (по умолчанию std :: vector ), и два итератора в начало и конец последовательности. В отличие от реальных контейнеров STL, он не позволяет итерация своих элементов (он строго придерживается своего абстрактного определения типа данных). В STL также есть служебные функции для управления другим контейнером с произвольным доступом в виде двоичной максимальной кучи. В Библиотеки Boost также есть реализация в куче библиотеки.
Python heapq модуль реализует двоичную минимальную кучу поверх списка.
Ява библиотека содержит PriorityQueue класс, который реализует очередь с минимальным приоритетом.
Scala библиотека содержит PriorityQueue класс, который реализует очередь с максимальным приоритетом.
Идти библиотека содержит контейнер / куча модуль, который реализует минимальную кучу поверх любой совместимой структуры данных.
В Стандартная библиотека PHP extension содержит класс SplPriorityQueue.
Apple Основной фундамент рамки содержат CFBinaryHeap структура, реализующая min-heap.
Приложения












Управление пропускной способностью
Очередь с приоритетом может использоваться для управления ограниченными ресурсами, такими как пропускная способность на линии передачи от сеть маршрутизатор. В случае исходящего трафик постановка в очередь из-за недостаточной пропускной способности, все другие очереди могут быть остановлены для отправки трафика из очереди с наивысшим приоритетом по прибытии. Это гарантирует, что приоритетный трафик (например, трафик в реальном времени, например, RTP поток VoIP connection) пересылается с наименьшей задержкой и наименьшей вероятностью отклонения из-за того, что очередь достигает максимальной емкости. Весь другой трафик можно обрабатывать, когда очередь с наивысшим приоритетом пуста. Другой используемый подход - отправка непропорционально большего объема трафика из очередей с более высоким приоритетом.
Многие современные протоколы для локальные сети также включить концепцию приоритетных очередей в контроль доступа к медиа (MAC) подуровень, чтобы гарантировать, что высокоприоритетные приложения (такие как VoIP или же IPTV ) имеют меньшую задержку, чем другие приложения, которые могут обслуживаться лучшее усилие служба. Примеры включают IEEE 802.11e (поправка к IEEE 802.11 который обеспечивает качество обслуживания ) и ITU-T G.hn (стандарт высокоскоростной локальная сеть с использованием существующей домашней электропроводки (линии электропередач, телефонные линии и коаксиальные кабели ).
Обычно устанавливается ограничение (ограничитель), чтобы ограничить полосу пропускания, которую может принимать трафик из очереди с наивысшим приоритетом, чтобы пакеты с высоким приоритетом не заглушали весь остальной трафик. Этот предел обычно никогда не достигается из-за экземпляров управления высокого уровня, таких как Cisco Callmanager, который может быть запрограммирован на запрет вызовов, превышающих запрограммированный предел пропускной способности.
Дискретное моделирование событий
Еще одно применение очереди с приоритетами - управление событиями в дискретное моделирование событий. События добавляются в очередь, и время их моделирования используется в качестве приоритета. Выполнение симуляции продолжается путем многократного вытягивания вершины очереди и выполнения на ней события.
Смотрите также: Планирование (вычисление), теория массового обслуживания
Алгоритм Дейкстры
Когда график хранится в виде список смежности или матрица, приоритетная очередь может использоваться для эффективного извлечения минимума при реализации Алгоритм Дейкстры, хотя также необходима возможность эффективного изменения приоритета конкретной вершины в очереди приоритетов.
Кодирование Хаффмана
Кодирование Хаффмана требует многократного получения двух самых низкочастотных деревьев. Очередь с приоритетом один из способов сделать это.
Алгоритмы поиска лучшего первого
Поиск лучшего первого алгоритмы, такие как Алгоритм поиска A *, найдите кратчайший путь между двумя вершины или же узлы из взвешенный график, пробуя в первую очередь наиболее перспективные маршруты. Приоритетная очередь (также известная как челка) используется для отслеживания неизведанных маршрутов; тот, для которого оценка (нижняя граница в случае A *) общей длины пути является наименьшей, получает высший приоритет. Если из-за нехватки памяти поиск лучшего в первую очередь невозможен, варианты, такие как SMA * вместо этого можно использовать алгоритм с двусторонняя приоритетная очередь чтобы разрешить удаление элементов с низким приоритетом.
Алгоритм триангуляции ROAM
Оптимально адаптирующиеся сетки в реальном времени (ROAM ) алгоритм вычисляет динамически изменяющуюся триангуляцию местности. Он работает, разделяя треугольники там, где требуется больше деталей, и объединяя их там, где требуется меньше деталей. Алгоритм присваивает каждому треугольнику на местности приоритет, обычно связанный с уменьшением ошибки, если этот треугольник будет разделен. Алгоритм использует две очереди приоритета: одну для треугольников, которые можно разделить, а другую для треугольников, которые можно объединить. На каждом шаге треугольник из очереди разделения с наивысшим приоритетом разделяется, или треугольник из очереди слияния с самым низким приоритетом объединяется со своими соседями.
Алгоритм Прима для минимального остовного дерева
С помощью очередь с приоритетом минимальной кучи в Алгоритм Прима найти минимальное остовное дерево из связаны и неориентированный граф, можно добиться хорошего времени работы. Эта очередь с минимальным приоритетом кучи использует структуру данных минимальной кучи, которая поддерживает такие операции, как вставлять, минимум, экстракт мин, клавиша уменьшения.[18] В этой реализации масса ребер используется для определения приоритета вершины. Чем меньше вес, тем выше приоритет и выше вес, тем ниже приоритет.[19]
Очередь с параллельным приоритетом












Распараллеливание может использоваться для ускорения очередей с приоритетом, но требует некоторых изменений в интерфейсе очереди с приоритетами. Причина таких изменений в том, что при последовательном обновлении обычно только  или же  стоимость, и нет никакой практической выгоды для распараллеливания такой операции. Одно из возможных изменений - разрешить одновременный доступ нескольких процессоров к одной и той же приоритетной очереди. Второе возможное изменение - разрешить пакетные операции, которые работают с  элементы, а не только один элемент. Например, extractMin удалит первый  элементы с наивысшим приоритетом.
Параллельный параллельный доступ
Если приоритетная очередь разрешает одновременный доступ, несколько процессов могут одновременно выполнять операции с этой приоритетной очередью. Однако здесь возникают две проблемы. Прежде всего, определение семантики отдельных операций больше не является очевидным. Например, если два процесса хотят извлечь элемент с наивысшим приоритетом, должны ли они получить один и тот же элемент или разные? Это ограничивает параллелизм на уровне программы, использующей очередь приоритетов. Кроме того, поскольку несколько процессов имеют доступ к одному и тому же элементу, это приводит к конфликту.
  
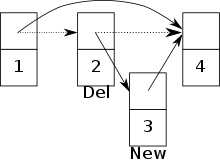Узел 3 вставлен и устанавливает указатель узла 2 на узел 3. Сразу после этого узел 2 удаляется, а указатель узла 1 устанавливается на узел 4. Теперь узел 3 больше недоступен.
Параллельный доступ к приоритетной очереди может быть реализован в модели PRAM с одновременным чтением и одновременной записью (CRCW). В дальнейшем приоритетная очередь реализована как пропустить список.[20][21] Кроме того, примитив атомарной синхронизации, CAS, используется для создания списка пропуска замок -свободный. Узлы списка пропуска состоят из уникального ключа, приоритета, множество из указатели, для каждого уровня, к следующим узлам и Удалить отметка. В Удалить отметка отмечает, что узел собирается быть удаленным процессом. Это гарантирует, что другие процессы могут соответствующим образом отреагировать на удаление.
  • вставить (е): Сначала создается новый узел с ключом и приоритетом. Кроме того, узлу назначается ряд уровней, что диктует размер массива указателей. Затем выполняется поиск, чтобы найти правильную позицию, в которую нужно вставить новый узел. Поиск начинается с первого узла и с самого высокого уровня. Затем список пропуска перемещается вниз до самого нижнего уровня, пока не будет найдена правильная позиция. Во время поиска для каждого уровня последний пройденный узел будет сохранен как родительский узел для нового узла на этом уровне. Кроме того, узел, на который указывает указатель на этом уровне родительского узла, будет сохранен как узел-преемник нового узла на этом уровне. Впоследствии для каждого уровня нового узла указатели родительского узла будут установлены на новый узел. Наконец, указатели для каждого уровня нового узла будут установлены на соответствующие узлы-преемники.
  • экстракт мин: Во-первых, список пропусков просматривается, пока не будет достигнут узел, чей Удалить отметка не установлена. Этот Удалить mark, чем установлено в true для этого узла. Наконец, обновляются указатели родительских узлов удаленного узла.
Если разрешен одновременный доступ к приоритетной очереди, между двумя процессами могут возникнуть конфликты. Например, конфликт возникает, если один процесс пытается вставить новый узел, но в то же время другой процесс собирается удалить предшественника этого узла.[20] Существует риск того, что новый узел будет добавлен в список пропуска, но станет недоступен. (См. Изображение )
K-элементные операции
В этом параметре операции с приоритетной очередью обобщаются на пакет  элементы. Например, k_extract-min удаляет  наименьшие элементы очереди приоритета и возвращает их. 
В настройка общей памяти, параллельная очередь приоритетов может быть легко реализована с помощью параллельной деревья двоичного поиска и древовидные алгоритмы на основе соединений. Особенно, k_extract-min соответствует расколоть на двоичном дереве поиска, имеющем  стоимость и дает дерево, которое содержит  мельчайшие элементы. k_insert может применяться союз исходной приоритетной очереди и пакета вставок. Если партия уже отсортирована по ключу, k_insert имеет  Стоимость. В противном случае нам нужно сначала отсортировать партию, поэтому стоимость составит . Аналогично могут применяться и другие операции для очереди с приоритетом. Например, k_decrease-key можно сделать, предварительно применив разница а потом союз, который сначала удаляет элементы, а затем вставляет их обратно с обновленными ключами. Все эти операции очень параллельны, а их теоретическую и практическую эффективность можно найти в соответствующих исследовательских работах.[22][23].
В оставшейся части этого раздела обсуждается алгоритм распределенной памяти на основе очередей. Мы предполагаем, что каждый процессор имеет свою собственную локальную память и локальную (последовательную) очередь приоритетов. Элементы глобальной (параллельной) очереди приоритета распределяются по всем процессорам.
  
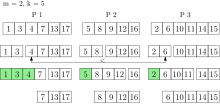k_extract-min выполняется в очереди с приоритетом с тремя процессорами. Зеленые элементы возвращаются и удаляются из очереди приоритетов.
А k_insert операция назначает элементы равномерно случайным образом процессорам, которые вставляют элементы в свои локальные очереди. Обратите внимание, что отдельные элементы все еще могут быть вставлены в очередь. При использовании этой стратегии наименьшие глобальные элементы находятся в объединении наименьших локальных элементов каждого процессора с высокой вероятностью. Таким образом, каждый процессор содержит репрезентативную часть очереди с глобальным приоритетом.
Это свойство используется, когда k_extract-min выполняется, как наименьшее  элементы каждой локальной очереди удаляются и собираются в результирующий набор. Элементы в наборе результатов по-прежнему связаны с их исходным процессором. Количество элементов  который удаляется из каждой локальной очереди, зависит от  и количество процессоров . [24]Путем параллельного отбора  определяются наименьшие элементы результирующего набора. С большой вероятностью это глобальные  мельчайшие элементы. Если не,  элементы снова удаляются из каждой локальной очереди и помещаются в набор результатов. Это делается до тех пор, пока глобальный  самые маленькие элементы находятся в наборе результатов. Теперь эти  элементы могут быть возвращены. Все остальные элементы набора результатов вставляются обратно в свои локальные очереди. Время работы k_extract-min ожидается , куда  и размер очереди приоритета.[24]
Очередь с приоритетом может быть дополнительно улучшена, если не перемещать оставшиеся элементы набора результатов непосредственно обратно в локальные очереди после k_extract-min операция. Это позволяет избежать постоянного перемещения элементов между набором результатов и локальными очередями.
Удалив сразу несколько элементов, можно значительно ускорить работу. Но не все алгоритмы могут использовать такую ​​приоритетную очередь. Например, алгоритм Дейкстры не может работать сразу на нескольких узлах. Алгоритм выбирает узел с наименьшим расстоянием от очереди приоритетов и вычисляет новые расстояния для всех его соседних узлов. Если бы вы вынули  узлы, работающие на одном узле, могут изменить расстояние до другого из  узлы. Таким образом, использование операций с k-элементами разрушает свойство установки метки алгоритма Дейкстры.
Смотрите также












Рекомендации












  1. ^ Кормен, Томас Х.; Лейзерсон, Чарльз Э.; Ривест, Рональд Л.; Штейн, Клиффорд (2001) [1990]. «Глава 20: Кучи Фибоначчи». Введение в алгоритмы (2-е изд.). MIT Press и McGraw-Hill. С. 476–497. ISBN  0-262-03293-7. Третье издание, с. 518.
  2. ^ Скиена, Стивен (2010). Руководство по разработке алгоритмов (2-е изд.). Springer Science + Business Media. ISBN  978-1-849-96720-4.
  3. ^ П. ван Эмде Боас. Сохранение порядка в лесу менее чем за логарифмическое время. В Материалы 16-го ежегодного симпозиума по основам компьютерных наук, страницы 75-84. Компьютерное общество IEEE, 1975.
  4. ^ Майкл Л. Фредман и Дэн Э. Уиллард. Превышение теоретической информационной границы с помощью деревьев слияния. Журнал компьютерных и системных наук, 48(3):533-551, 1994
  5. ^ а б c d Кормен, Томас Х.; Лейзерсон, Чарльз Э.; Ривест, Рональд Л. (1990). Введение в алгоритмы (1-е изд.). MIT Press и McGraw-Hill. ISBN  0-262-03141-8.
  6. ^ "Биномиальная куча | Блестящая вики по математике и науке". brilliant.org. Получено 2019-09-30.
  7. ^ Фредман, Майкл Лоуренс; Тарджан, Роберт Э. (Июль 1987 г.). «Кучи Фибоначчи и их использование в улучшенных алгоритмах оптимизации сети» (PDF). Журнал Ассоциации вычислительной техники. 34 (3): 596–615. CiteSeerX  10.1.1.309.8927. Дои:10.1145/28869.28874.
  8. ^ Яконо, Джон (2000), «Улучшенные верхние границы для парных куч», Proc. 7-й скандинавский семинар по теории алгоритмов (PDF), Конспект лекций по информатике, 1851, Springer-Verlag, стр. 63–77, arXiv:1110.4428, CiteSeerX  10.1.1.748.7812, Дои:10.1007 / 3-540-44985-X_5, ISBN  3-540-67690-2
  9. ^ Фредман, Майкл Лоуренс (Июль 1999 г.). «Об эффективности объединения куч и связанных структур данных» (PDF). Журнал Ассоциации вычислительной техники. 46 (4): 473–501. Дои:10.1145/320211.320214.
  10. ^ Петти, Сет (2005). К окончательному анализу парных куч (PDF). FOCS '05 Материалы 46-го ежегодного симпозиума IEEE по основам информатики. С. 174–183. CiteSeerX  10.1.1.549.471. Дои:10.1109 / SFCS.2005.75. ISBN  0-7695-2468-0.
  11. ^ Бродал, Герт С. (1996), "Очереди приоритетов наихудшего случая" (PDF), Proc. 7-й ежегодный симпозиум ACM-SIAM по дискретным алгоритмам, стр. 52–58
  12. ^ Гудрич, Майкл Т.; Тамассия, Роберто (2004). «7.3.6. Строительство кучи снизу вверх». Структуры данных и алгоритмы в Java (3-е изд.). С. 338–341. ISBN  0-471-46983-1.
  13. ^ Хёуплер, Бернхард; Сен, Сиддхартха; Тарджан, Роберт Э. (Ноябрь 2011 г.). "Куча ранговых пар" (PDF). SIAM J. Computing. 40 (6): 1463–1485. Дои:10.1137/100785351.
  14. ^ Бродал, Герт Стёльтинг; Лагогианнис, Джордж; Тарджан, Роберт Э. (2012). Строгие груды Фибоначчи (PDF). Материалы 44-го симпозиума по теории вычислений - STOC '12. С. 1177–1184. CiteSeerX  10.1.1.233.1740. Дои:10.1145/2213977.2214082. ISBN  978-1-4503-1245-5.
  15. ^ Такаока, Тадао (1999), Теория 2–3 куч (PDF), п. 12
  16. ^ Торуп, Миккель (2007). «Равнозначность приоритетных очередей и сортировки». Журнал ACM. 54 (6): 28. Дои:10.1145/1314690.1314692. S2CID  11494634.
  17. ^ «Архивная копия» (PDF). В архиве (PDF) из оригинала 2011-07-20. Получено 2011-02-10.CS1 maint: заархивированная копия как заголовок (связь)
  18. ^ Кормен, Томас Х.; Лейзерсон, Чарльз Э.; Ривест, Рональд Л.; Штейн, Клиффорд (2009) [1990]. Введение в алгоритмы (3-е изд.). MIT Press и McGraw-Hill. ISBN  0-262-03384-4.
  19. ^ «Алгоритм Прима». Компьютерщик для компьютерных фанатов. В архиве из оригинала от 9 сентября 2014 г.. Получено 12 сентября 2014.
  20. ^ а б Сунделл, Хокан; Цигас, Филиппы (2005). «Быстрые параллельные очереди приоритетов без блокировок для многопоточных систем». Журнал параллельных и распределенных вычислений. 65 (5): 609–627. Дои:10.1109 / IPDPS.2003.1213189. S2CID  20995116.
  21. ^ Линден, Йонссон (2013), «Очередь с одновременным приоритетом на основе Skiplist с минимальной конкуренцией за память», Технический отчет 2018-003 (на немецком)
  22. ^ Blelloch, Guy E .; Феризович, Даниэль; Сунь, Ихан (2016), «Просто присоединяйтесь к параллельным упорядоченным множествам», Симпозиум по параллельным алгоритмам и архитектурам, Proc. 28-го симпозиума ACM. Параллельные алгоритмы и архитектуры (SPAA 2016), ACM, стр. 253–264, arXiv:1602.02120, Дои:10.1145/2935764.2935768, ISBN  978-1-4503-4210-0, S2CID  2897793
  23. ^ Blelloch, Guy E .; Феризович, Даниэль; Sun, Yihan (2018), "PAM: параллельные дополненные карты", Материалы 23-го симпозиума ACM SIGPLAN по принципам и практике параллельного программирования, ACM, стр. 290–304.
  24. ^ а б Сандерс, Питер; Мельхорн, Курт; Дицфельбингер, Мартин; Дементьев, Роман (2019). Последовательные и параллельные алгоритмы и структуры данных - Basic Toolbox. Издательство Springer International. С. 226–229. Дои:10.1007/978-3-030-25209-0. ISBN  978-3-030-25208-3. S2CID  201692657.
дальнейшее чтение












внешняя ссылка