Многоугольная цепочка - Polygonal chain

Простая многоугольная цепочка

Самопересекающаяся многоугольная цепь

Замкнутая многоугольная цепочка

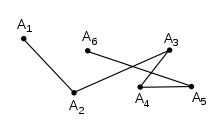
В геометрия, а многоугольная цепь это связная серия отрезки линии. Более формально многоугольная цепочка п это изгиб указанный последовательность очков ${displaystyle scriptstyle (A_{1},A_{2},dots ,A_{n})}$ назвал его вершины. Сама кривая состоит из отрезков прямых, соединяющих последовательные вершины.

Имя

Полигональную цепочку также можно назвать ломаная кривая,^[1] многоугольный путь,^[2] ломаная линия,^[3] кусочно-линейная кривая,^[3] пунктирная линия^[4] или в географические информационные системы, а линия или же линейное кольцо.^[5]

Вариации

А простая многоугольная цепочка - это тот, в котором пересекаются только последовательные (или первый и последний) сегменты и только в своих конечных точках.

А замкнутая многоугольная цепь - это вершина, в которой первая вершина совпадает с последней, или, альтернативно, первая и последняя вершины также соединены отрезком прямой.^[6] Простая замкнутая многоугольная цепочка в самолет граница простой многоугольник. Часто термин "многоугольник "используется в значении" замкнутая многоугольная цепочка ", но в некоторых случаях важно проводить различие между многоугольная область и многоугольная цепь.

Полигональная цепь называется монотонный, если есть прямая линия L так что каждая линия, перпендикулярная L не более одного раза пересекает цепочку. Всякая нетривиальная монотонная ломаная открыта. Для сравнения: монотонный многоугольник представляет собой многоугольник (замкнутую цепь), который можно разбить ровно на две монотонные цепи.^[7] Графики кусочно-линейные функции образуют монотонные цепочки относительно горизонтальной линии.

Набор п= 17 точек имеет многоугольный путь с 4 наклонами одного знака

Характеристики

Каждый набор не менее ${displaystyle n}$ точек содержит многоугольный путь не менее ${displaystyle lfloor {sqrt {n-1}}floor }$ края, у которых все откосы имеют одинаковый знак. Это следствие Теорема Эрдеша – Секереса.

Приложения

Многоугольные цепочки часто можно использовать для аппроксимации более сложных кривых. В этом контексте Алгоритм Рамера – Дугласа – Пекера может использоваться для поиска многоугольной цепи с несколькими сегментами, которая служит точным приближением.^[8][9]

В рисунок графика полигональные цепочки часто используются для представления ребер графов в стилях рисования, где рисование ребер в виде отрезков прямых линий может вызвать пересечения, столкновения ребер с вершинами или другие нежелательные особенности. В этом контексте часто желательно рисовать края с минимальным количеством сегментов и изгибов, чтобы уменьшить визуальный беспорядок на чертеже; проблема минимизации количества изгибов называется минимизация изгиба.^[10]

Многоугольные цепочки также являются фундаментальным типом данных в вычислительная геометрия. Например, точка расположения алгоритм Ли и Препарата действует путем разложения произвольных планарные подразделения в упорядоченную последовательность монотонных цепочек, в которой проблема запроса местоположения точки может быть решена с помощью бинарный поиск; Позже этот метод был усовершенствован, чтобы дать оптимальные временные рамки для задачи определения местоположения точки.^[11]

С географическая информационная система, линии могут представлять любую линейную геометрию и могут быть описаны с помощью известный текст разметка как LineString или же MultiLineString.^[5] Линейные кольца (или LinearRing) - это замкнутые и простые многоугольные цепи, используемые для построения геометрии многоугольника.

Смотрите также

• Цепь (алгебраическая топология), формальная комбинация симплексов, которая в одномерном случае включает многоугольные цепи
• Составная кривая Безье, обобщение, заменяющее каждую прямую многоугольной цепи гладкой кривой.
• Расстояние ссылки, количество сегментов кратчайшей цепи, соединяющей две точки в многоугольнике.
• Кусочная регрессия
• Путь (теория графов), аналогичное понятие в абстрактных графах
• Многогранный рельеф, трехмерное обобщение монотонной многоугольной цепи
• Номер палки, инвариант узла, основанный на представлении узла в виде замкнутой многоугольной цепи
• Траверс, приложение в геодезия

Рекомендации

1. Гомес, Йонас; Велью, Луис; Коста Соуза, Марио (2012), Компьютерная графика: теория и практика, CRC Press, стр. 186, ISBN  9781568815800.
2. Чейни, Уорд (2001), Анализ для прикладной математики, Тексты для выпускников по математике, 208, Springer, стр. 13, ISBN  9780387952796.
3. Буассонна, Жан-Даниэль; Тейо, Моник (2006), Эффективная вычислительная геометрия для кривых и поверхностей, Springer, стр. 34, ISBN  9783540332596.
4. Муггео, Вито М. Р. (май 2008 г.), «сегментированный: пакет R для соответствия моделям регрессии с ломаной линией» (PDF), Новости R, 8 (1): 20–25
5. Открытый геопространственный консорциум (2011-05-28), Херринг, Джон Р. (ред.), Стандарт реализации OpenGIS® для географической информации - Простой доступ к функциям - Часть 1: Общая архитектура, 1.2.1, Открытый геопространственный консорциум, получено 2016-01-15
6. Мельхорн, Курт; Нахер, Стефан (1999), LEDA: платформа для комбинаторных и геометрических вычислений, Cambridge University Press, стр. 758, г. ISBN  9780521563291.
7. О'Рурк, Джозеф (1998), Вычислительная геометрия в C, Кембриджские трактаты по теоретической информатике, издательство Кембриджского университета, стр. 45, ISBN  9780521649766.
8. Рамер, Урс (1972), "Итерационная процедура для полигональной аппроксимации плоских кривых", Компьютерная графика и обработка изображений, 1 (3): 244–256, Дои:10.1016 / S0146-664X (72) 80017-0.
9. Дуглас, Дэвид; Пекер, Томас (1973), "Алгоритмы уменьшения количества точек, необходимых для представления оцифрованной линии или ее карикатуры", Канадский картограф, 10 (2): 112–122, Дои:10.3138 / FM57-6770-U75U-7727.
10. Тамассия, Роберто (1987), «О вложении графа в сетку с минимальным числом изгибов», SIAM Журнал по вычислениям, 16 (3): 421–444, Дои:10.1137/0216030.
11. Эдельсбруннер, Герберт; Гибас, Леонидас Дж.; Столфи, Хорхе (1986), «Оптимальное расположение точки в монотонном подразделении», SIAM Журнал по вычислениям, 15 (2): 317–340, Дои:10.1137/0215023.