Планарная алгебра - Planar algebra
В математика, плоские алгебры впервые появился в работе Воан Джонс на стандартный инвариант из II1 субфактор.[1] Они также обеспечивают подходящую алгебраическую основу для многих инварианты узлов (в частности Многочлен Джонса ), и использовались при описании свойств Гомологии Хованова относительно клубок сочинение.[2][3] Любая субфакторная планарная алгебра обеспечивает семейство унитарных представлений Группы Томпсона.[4]Любую конечную группу (и квантовое обобщение) можно закодировать как плоскую алгебру.[1]
Определение
Идея плоской алгебры заключается в схематической аксиоматизации стандартный инвариант.[1][5][6]
Плоский клубок
А (затемненный) плоский клубок это данные конечного числа Вход диски, один выход диск, непересекающиеся строки, дающие четное число, скажем , интервалов на диск и один -отмеченный интервал на диск.

Здесь метка отображается как -форма. На каждом входном диске он помещается между двумя соседними исходящими строками, а на выходном диске он помещается между двумя соседними входящими строками. Плоский клубок определяется с точностью до изотопия.
Сочинение
К сочинять два плоских клубка, поместите выходной диск одного во вход другого, имеющий столько же интервалов, одинаковую штриховку отмеченных интервалов и такой, чтобы -отмеченные интервалы совпадают. Наконец, удаляем совпадающие круги. Обратите внимание, что два плоских клубка могут иметь ноль, один или несколько возможных составов.

Планарная операда
В планарная операда - множество всех плоских клубков (с точностью до изоморфизма) с такими композициями.
Планарная алгебра
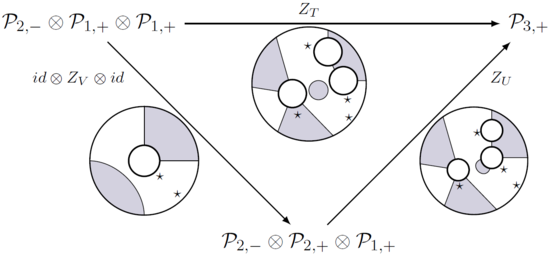
А планарная алгебра это представление планарной операды; точнее, это семейство векторных пространств , называется -боксы, на которых действует плоская операда, т.е.для любого клубка (с одним выходным диском и входные диски с и интервалы соответственно) имеется полилинейная карта
с по затенению -отмеченные интервалы, и эти карты (также называемые статистическими суммами) учитывают состав клубка таким образом, что все диаграммы, как показано ниже, коммутируют.
Примеры
Плоские клубки
Семейство векторных пространств порожденные плоскими клубками, имеющими интервалы на их выход диск и белый (или черный) -отмеченный интервал, допускает структуру плоской алгебры.
Темперли – Либ
Планарная алгебра Темперли-Либа порождается плоскими клубками без входного диска; это -box пространство генерируется

Более того, замкнутая строка заменяется умножением на .

Обратите внимание, что размер это Каталонский номер Эта плоская алгебра кодирует понятие Алгебра Темперли – Либа.
Алгебра Хопфа
Полупростой и непростой Алгебра Хопфа над алгебраически замкнутым полем кодируется в плоской алгебре, определяемой образующими и соотношениями, и «соответствует» (с точностью до изоморфизма) связной, неприводимой, сферической, невырожденной плоской алгебре с ненулевым модулем и глубины два.[7]
Обратите внимание, что связаны средства (что касается оцениваемый ниже), несводимый средства , сферический определено ниже, а невырожденный означает, что следы (определенные ниже) невырождены.
Подфакторная планарная алгебра
Определение
А субфакторная планарная алгебра плоский -алгебра который:
- (1) Конечномерные:
- (2) Оценка:
- (3) Сферический:
- (4) Положительный: определяет внутренний продукт.
Обратите внимание, что согласно (2) и (3) любая замкнутая строка (заштрихованная или нет) считается одной и той же константой. .

Действие путаницы имеет дело с сопряженным:
с зеркальное отображение и примыкающий к в .
Примеры и результаты
Теорема об отсутствии призраков: Планарная алгебра не имеет призрака (т.е. элемента с ) если и только если
За как указано выше, пусть быть нулевым идеалом (порожденным элементами с ). Тогда частное является субфакторной планарной алгеброй, называемой Подфакторная планарная алгебра Темперли – Либа-Джонса . Любая субфакторная планарная алгебра с константой признает как плоская подалгебра.
Плоская алгебра является субфакторной планарной алгеброй тогда и только тогда, когда это стандартный инвариант экстремального субфактор индекса , с и .[8][9][10]Конечная глубина или неприводимый субфактор экстремальна ( на ).
Существует субфакторная планарная алгебра, кодирующая любую конечную группу (и, в более общем смысле, любую конечномерную Хопф -алгебра, называемая алгеброй Каца), определяемая образующими и соотношениями. (Конечномерная) алгебра Каца «соответствует» (с точностью до изоморфизма) неприводимой субфакторной планарной алгебре глубины два.[11][12]
Подфакторная планарная алгебра, связанная с включением конечных групп,[13] не всегда запоминает включение (без ядра).[14][15]
Подфакторная плоская алгебра Биша-Джонса (иногда называемый суетливо-каталонским) определяется как но разрешив два цвета строки с их собственной константой и , с как указано выше. Это плоская подалгебра любой субфакторной планарной алгебры с таким промежуточным звеном, что и . [16][17]
Первый субфактор конечной глубины планарной алгебры индекса называется Haagerup субфакторная планарная алгебра.[18] Имеет индекс .
Подфакторные планарные алгебры полностью классифицируются по индексу не более [19]и немного дальше.[20]Эта классификация была инициирована Уффе Хаагеруп.[21]Он использует (среди прочего) список возможных основных графов вместе с теоремой вложения[22]и алгоритм медузы.[23]
Подфакторная планарная алгебра запоминает подфактор (то есть его стандартный инвариант завершен), если он поддается.[24] Подфактор конечной глубины является приемлемым.
О неаменабельном случае: существует неклассифицируемое множество неприводимых гиперконечных подфакторов индекса 6, которые все имеют один и тот же стандартный инвариант.[25]
Преобразование Фурье и бипроекции
Позволять - субфактор конечного индекса, и соответствующая подфакторная планарная алгебра. Предположить, что неприводимо (т.е. ). Позволять быть промежуточным субфактором. Пусть проекция Джонса . Обратите внимание, что . Позволять и .
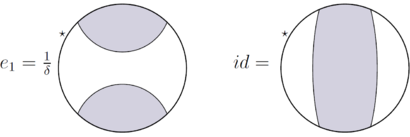
Обратите внимание, что и .
Пусть биективное линейное отображение быть преобразование Фурье, также называемый -щелкните (внешней звезды) или вращение; и разреши быть сопродукт из и .

Обратите внимание, что слово сопродукт является уменьшительным от продукт свертки. Это бинарная операция.
Копроизведение удовлетворяет равенству
Для любых положительных операторов , побочный продукт тоже положительный; это можно увидеть схематически:[26]

Позволять быть противоположный (также называемый вращение). Карта соответствует четырем - щелчки внешней звезды, так что это карта идентичности, а затем .
В случае алгебры Каца контрагредиент - это в точности антипод,[12] которые для конечной группы соответствуют обратному.
А двупроекция это проекция с кратное проекции. Обратите внимание, что и бипроекции; это можно увидеть следующим образом:

Проекция является бипроекцией, если и только если это проекция Джонса промежуточного субфактора [27], если и только если .[28][26]
Переписка Галуа:[29] в случае алгебры Каца бипроекции равны 1-1 с левыми коидеальными подалгебрами, которые для конечной группы соответствуют подгруппам.
Для любой неприводимой субфакторной планарной алгебры множество бипроекторов представляет собой конечную решетку, [30] формы , как для интервала конечных групп .
Используя бипроекции, мы можем сделать промежуточные субфакторные алгебры планарными. [31][32]
В принцип неопределенности распространяется на любую неприводимую подфакторную планарную алгебру :
Позволять с проекция дальности и ненормализованный след (т.е. на ).
Принцип некоммутативной неопределенности: [33] Позволять , ненулевое. потом
Предполагая и положительный, равенство выполняется тогда и только тогда, когда это двупроекция. В более общем смысле равенство выполняется тогда и только тогда, когда это двухсменный двупроекции.
Рекомендации
- ^ а б c Воан Ф. Р. Джонс (1999), "Планарные алгебры, I", arXiv:математика / 9909027
- ^ "Дрор Бар-Натан: Публикации: Кобордизмы". Math.toronto.edu. Дои:10.2140 / gt.2005.9.1443. Получено 2016-11-20.
- ^ "Фронт: [math / 0410495] Гомологии Хованова для клубков и кобордизмов". Front.math.ucdavis.edu. Дои:10.2140 / gt.2005.9.1443. Получено 2016-11-20.
- ^ Воан Ф. Р. Джонс (2017), «Некоторые унитарные представления групп Томпсона F и T», J. Comb. Алгебра, 1 (1): 1–44, arXiv:1412.7740, Дои:10.4171 / JCA / 1-1-1, МИСТЕР 3589908
- ^ Виджай Кодиялам, ПРОТИВ. Раскол (2004), «О планарных алгебрах Джонса», J. Разветвления теории узлов, 13 (2): 219–247, Дои:10.1142 / S021821650400310X, МИСТЕР 2047470CS1 maint: использует параметр авторов (связь)
- ^ "Виджай Кодиялам - Планарные алгебры - IMSc 2015". youtube.com. 2015-11-14.
- ^ Виджай Кодиялам, ПРОТИВ. Раскол (2006), "Планарная алгебра полупростой и косвенно-простой алгебры Хопфа", Proc. Индийский акад. Sci. Математика. Sci., 116 (4): 1–16, arXiv:математика / 0506153, Bibcode:2005математика ...... 6153KCS1 maint: использует параметр авторов (связь)
- ^ Сорин Попа (1995), "Аксиоматизация решетки высших относительных коммутантов подфактора", Inventiones Mathematicae, 120 (3): 427–445, Bibcode:1995ИнМат.120..427П, Дои:10.1007 / BF01241137, МИСТЕР 1334479
- ^ Алиса Гионнет, Воан Ф. Р. Джонс, Дмитрий Шляхтенко (2010), «Случайные матрицы, свободная вероятность, плоские алгебры и субфакторы», Clay Math. Proc., {11}: 201–239, МИСТЕР 2732052CS1 maint: использует параметр авторов (связь)
- ^ Виджай Кодиялам, ПРОТИВ. Раскол (2009), «От субфакторных планарных алгебр к субфакторам», Междунар. J. Math., 20 (10): 1207–1231, arXiv:0807.3704, Дои:10.1142 / S0129167X0900573X, МИСТЕР 2574313CS1 maint: использует параметр авторов (связь)
- ^ Парамита Дас, Виджай Кодиялам (2005), «Планарные алгебры и теорема Окнеану-Шимански», Proc. Амер. Математика. Soc., 133 (9): 2751–2759, Дои:10.1090 / S0002-9939-05-07789-0, ISSN 0002-9939, МИСТЕР 2146224CS1 maint: использует параметр авторов (связь)
- ^ а б Виджай Кодиялам, Зеф Ландау, ПРОТИВ. Раскол (2003), "Плоская алгебра, ассоциированная с алгеброй Каца", Proc. Индийский акад. Sci. Математика. Sci., 113 (1): 15–51, Дои:10.1007 / BF02829677, ISSN 0253-4142, МИСТЕР 1971553CS1 maint: использует параметр авторов (связь)
- ^ Вед Пракаш Гупта (2008), «Планарная алгебра подгруппы-подфактора», Труды математических наук, 118 (4): 583–612, arXiv:0806.1791, Bibcode:2008arXiv0806.1791G, Дои:10.1007 / s12044-008-0046-0
- ^ Виджай Кодиялам, ПРОТИВ. Раскол (2000), «Подгруппа-подфактор», Математика. Сканд., 86 (1): 45–74, Дои:10.7146 / math.scand.a-14281, ISSN 0025-5521, МИСТЕР 1738515CS1 maint: использует параметр авторов (связь)
- ^ Масаки Идзуми (2002), "Характеризация изоморфных групп-подгрупп подфакторов", Int. Математика. Res. Нет., 2002 (34): 1791–1803, Дои:10.1155 / S107379280220402X, ISSN 1073-7928, МИСТЕР 1920326
- ^ Дитмар Биш, Воан Джонс (1997), "Алгебры, ассоциированные с промежуточными субфакторами", Inventiones Mathematicae, 128 (1): 89–157, Bibcode:1997InMat.128 ... 89J, Дои:10.1007 / s002220050137CS1 maint: использует параметр авторов (связь)
- ^ Пинхас Гроссман, Воан Джонс (2007), «Промежуточные субфакторы без дополнительной структуры», J. Amer. Математика. Soc., 20 (1): 219–265, Bibcode:2007JAMS ... 20..219G, Дои:10.1090 / S0894-0347-06-00531-5, МИСТЕР 2257402CS1 maint: использует параметр авторов (связь)
- ^ Эмили Петерс (2010), "Конструкция плоской алгебры субфактора Хаагерупа", Междунар. J. Math., 21 (8): 987–1045, arXiv:0902.1294, Дои:10.1142 / S0129167X10006380, МИСТЕР 2679382
- ^ Воан Ф. Р. Джонс, Скотт Моррисон, Ноа Снайдер (2014), «Классификация субфакторов индекса не более ", Бык. Амер. Математика. Soc. (Н.С.), 51 (2): 277–327, arXiv:1304.6141, Дои:10.1090 / S0273-0979-2013-01442-3, МИСТЕР 3166042CS1 maint: использует параметр авторов (связь)
- ^ Нарджесс Афзали, Скотт Моррисон, Дэвид Пенни (2015), Классификация субфакторов с индексом не выше , стр. 70pp, arXiv:1509.00038, Bibcode:2015arXiv150900038ACS1 maint: использует параметр авторов (связь)
- ^ Уффе Хаагеруп (1994), "Основные графики субфакторов в диапазоне индекса ", Субфакторы (Кьюзесо, 1993): 1–38, МИСТЕР 1317352
- ^ Воан Джонс, Дэвид Пенни (2011), "Теорема вложения для субфакторных плоских алгебр конечной глубины", Квантовый тополь., 2 (3): 301–337, arXiv:1007.3173, Дои:10.4171 / QT / 23, МИСТЕР 2812459CS1 maint: использует параметр авторов (связь)
- ^ Стивен Бигелоу, Дэвид Пенни (2014), «Стабильность главного графа и алгоритм медузы». Математика. Анна., 358 (1–2): 1–24, arXiv:1208.1564, Дои:10.1007 / s00208-013-0941-2, МИСТЕР 3157990CS1 maint: использует параметр авторов (связь)
- ^ Попа, Сорин (1994), «Классификация аменабильных субфакторов типа II», Acta Mathematica, 172 (2): 163–255, Дои:10.1007 / BF02392646, МИСТЕР 1278111
- ^ Арно Бротье, Стефан Ваес (2015), «Семейства гиперконечных субфакторов с одинаковым стандартным инвариантом и заданной фундаментальной группой», J. Noncommut. Геом., 9 (3): 775–796, arXiv:1309.5354, Дои:10.4171 / JNCG / 207, МИСТЕР 3420531CS1 maint: использует параметр авторов (связь)
- ^ а б Чжэнвэй Лю (2016), "Планарные алгебры малого ранга с обменными отношениями", Пер. Амер. Математика. Soc., 368 (12): 8303–8348, arXiv:1308.5656, Дои:10.1090 / tran / 6582, ISSN 0002-9947, МИСТЕР 3551573
- ^ Дитмар Биш (1994), "Заметка о промежуточных субфакторах", Pacific J. Math., 163 (2): 201–216, Дои:10.2140 / pjm.1994.163.201, ISSN 0030-8730, МИСТЕР 1262294
- ^ Зеф А. Ландау (2002), "Планарные алгебры обменных отношений", Геом. Dedicata, 95: 183–214, Дои:10.1023 / А: 1021296230310, ISSN 0046-5755, МИСТЕР 1950890
- ^ Масаки Идзуми, Роберто Лонго, Сорин Попа (1998), "Соответствие Галуа для компактных групп автоморфизмов алгебр фон Неймана с обобщением на алгебры Каца", J. Funct. Анальный., 155 (1): 25–63, Дои:10.1006 / jfan.1997.3228, ISSN 0022-1236, МИСТЕР 1622812CS1 maint: использует параметр авторов (связь)
- ^ Ясуо Вататани (1996), "Решетки промежуточных субфакторов", J. Funct. Анальный., 140 (2): 312–334, Дои:10.1006 / jfan.1996.0110, HDL:2115/68899, ISSN 0022-1236, МИСТЕР 1409040
- ^ Зеф А. Ландау (1998), "Промежуточные субфакторы", Диссертация - Калифорнийский университет в Беркли: 132 пикселей
- ^ Кешаб Чандра Бакши (2016), Повторный визит к промежуточной плоской алгебре, стр. 31pp, arXiv:1611.05811, Bibcode:2016arXiv161105811B
- ^ Чунлан Цзян, Чжэнвэй Лю, Цзиньсон Ву (2016), «Принципы некоммутативной неопределенности», J. Funct. Анальный., 270 (1): 264–311, arXiv:1408.1165, Дои:10.1016 / j.jfa.2015.08.007CS1 maint: использует параметр авторов (связь)































![{ displaystyle delta in {2 cos ( pi /n)|n=3,4,5,...}cup [2, + infty]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0105ecf9dfad64e9ef7d45b51a545b2840b9f76f)






![{ Displaystyle [M: N] = дельта ^ {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d55dae0dce15dae9ad044ba8895fdaff5d20ad73)









![{ Displaystyle [К: N] = дельта _ {1} ^ {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59492aa33355cf94b9b676f6256c24200de16132)
![{ displaystyle [M: K] = delta _ {2} ^ {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ccf8855a8faf2ba1cde91d3af7db8ea17992a84a)











![{ displaystyle tr (e_ {1}) = delta ^ {- 2} = [M: N] ^ {- 1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9fd63195a24be73213cac05d2a89830dd84f65db)


















![{ displaystyle [e_ {1}, id]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a75ffda9959472ef1ddde2d3917fc81476c2feda)
![{ displaystyle [H, G]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca68a38294795a54c3f9e6dcbf49f347fc7253a7)










![{ displaystyle 4 <[M: N] <3 + { sqrt {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d04846369028bc2ae735583ba658fd316f8226e)