О равновесии плоскостей - On the Equilibrium of Planes

Плутарх представил Архимеда заявлением, что Любой заданный вес может быть перемещен заданной силой.

О равновесии плоскостей (Греческий: Περὶ ἐπιπέδων ἱσορροπιῶν) является трактатом Архимед в двух томах. Первая книга устанавливает закон рычага, и определяет центр тяжести треугольник и трапеция.^[1][2] В соответствии с Папп Александрийский, Архимед Работа с рычагами заставила его заметить: «Дайте мне место, на котором я буду стоять, и я сдвину Землю». (Греческий: δῶς μοι πᾶ στῶ καὶ τὰν γᾶν κινάσω).^[3] Вторая книга, содержащая десять предложений, исследует центры тяжести параболических сегментов.^[1]

Структура текста

Книга первая содержит пятнадцать предложений с семью постулатами. В предложении шесть Архимед устанавливает закон рычага, делая вывод, что «величины находятся в равновесии на расстояниях, обратно пропорциональных их весу». В предложениях десять и четырнадцать соответственно Архимед определяет центр тяжести параллелограмм и треугольник. Кроме того, в предложении 15 он устанавливает центр тяжести трапеция. Вторая книга, содержащая десять предложений, исследует исключительно параболические сегменты. Он исследует эти сегменты, заменяя их прямоугольниками одинаковой площади; обмен стал возможным благодаря результатам, полученным в Квадратура параболы.^[1][2]

Основная теорема

Архимед 'доказательство закон рычага выполняется в рамках шестого предложения. Он предназначен только для соизмеримых величин и опирается на предложения четыре, пять и один постулат.^[2]

Вступление

Равные веса на равных расстояниях.

В одном постулате Архимед утверждает, что «равные веса на равных расстояниях находятся в равновесии» (что означает один равный вес с каждой стороны плеча рычага). В предложениях 4 и 5 он расширяет это наблюдение, включив в него концепцию центр тяжести; при этом доказано, что центр тяжести любой системы, состоящей из четного числа равных грузов, равномерно распределенных, будет располагаться в средней точке между двумя центральными грузами (следовательно, вводятся несколько грузов с обеих сторон плеча рычага).

Заявление

Гири и рычаги в соотношении четыре к трем.

Учитывая два неравных, но соизмеримых веса и плечо рычага, разделенное на две неравные, но соизмеримые части (см. Рисунок напротив), в предложении шесть просто говорится, что если величины A и B применяются в точках E и D, соответственно, система будет быть в равновесии, если веса обратно пропорциональны длинам:

${\displaystyle A:B=CD:EC\,}$

Доказательство

Поэтому предположим, что линии и веса построены так, чтобы подчиняться правилу, с использованием общей меры (или единицы) N и в соотношении четыре к трем (согласно эскизу). Теперь удвойте длину ED, продублировав более длинную руку слева и более короткую руку справа.

Для демонстрации измените порядок строк так, чтобы CD находился рядом с LE (две красные линии вместе), и сопоставьте с оригиналом (как показано ниже):

Гири и рычаги в соотношении восемь к шести.

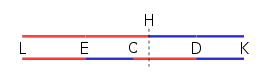
Тогда ясно, что обе линии в два раза длиннее исходной линии ED, что центр LH находится в точке E (см. Смежные красные линии), а центр HK находится в точке D. Кроме того, обратите внимание, что EH (которая равна CD) несет общий делитель (или единицу) N, точное количество раз, как и EC, и, следовательно, по логике, CH тоже. Затем остается доказать, что центр тяжести A, приложенного в E, и B, приложенного в D, будет иметь центр тяжести в C.

Следовательно, поскольку отношение LH к HK составляет не четыре к трем, а восемь к шести, аналогичным образом разделите величины A и B (преобразование, сохраняющее их исходное соотношение четыре к трем) и выровняйте их согласно диаграмме напротив. A с центром в E, а B с центром в D.

Теперь, поскольку четное количество равных гирь, расположенных на равном расстоянии, имеет центр тяжести между двумя средними гирями, A фактически применяется в E, а B в D, как того требует предложение. Кроме того, вся система состоит из четного числа равных весов, равномерно распределенных, и, следовательно, по тому же закону C должен быть центром тяжести всей системы. Таким образом, A, нанесенный в E, и B, примененный в D, имеют центр тяжести в C.^[1]

Подлинность

Хотя подлинность второй книги не вызывает сомнений, ряд исследований выявили несоответствия в презентации первой книги.^[2][4][5] Берггрен, в частности, ставит под сомнение обоснованность первой книги в целом; подчеркивая, среди прочего, избыточность предложений с первого по три, одиннадцать и двенадцать.^[2] Однако Берггрен следует Dijksterhuis, отвергая Мах Критика предложения шесть. Кроме того, его истинное значение заключается в том факте, что он демонстрирует, что «если система грузов, подвешенная на бревне, находится в равновесии, когда поддерживается в определенной точке, то любое перераспределение этих грузов, которое сохраняет их общий центр тяжести, также сохраняет равновесие ".^[2][4] Кроме того, седьмое предложение является неполным в его нынешнем виде, поэтому первая книга демонстрирует закон рычага только для соизмеримых величин.^[1][2][4]

Рекомендации

1. Хит, Т. «Сочинения Архимеда (1897 г.). Полное собрание сочинений в формате PDF (19 МБ)». Archive.org. В архиве из оригинала от 6 октября 2007 г.. Получено 2013-01-06.
2. Джон Леннарт Берггрен (1976). "Ложные теоремы в Архимедовом равновесии плоскостей Книга I". Архив истории точных наук 16 (2), 87-103. ISSN  1432-0657.
3. Цитируется Папп Александрийский в Синагога, Книга VIII
4. Dijksterhuis, E.J. (1987). Архимед. Издательство Принстонского университета, Принстон. ISBN  0-691-08421-1. Переизданный перевод исследования Архимеда и его работ 1938 года историком науки.
5. Мах, Э. (1907). Наука механика: критический и исторический отчет о ее развитии. Открытый суд, Чикаго. Переизданный перевод оригинала 1883 г. Томас Дж. МакКормак. Эд. 3, ред.