Отрицательная температура - Negative temperature

SI Шкала преобразования температуры / холода: температуры по шкале Кельвина показаны синим (шкала Цельсия - зеленым, шкала Фаренгейта - красным), значения холода в гигабайтах на наноджоуль показаны черным. Бесконечная температура (ноль холода) показана вверху диаграммы; положительные значения холода / температуры находятся справа, отрицательные значения - слева.

Определенный системы может достичь отрицательная термодинамическая температура; то есть их температура можно выразить как отрицательный количество на Кельвин или же Ренкин напольные весы. Это следует отличать от температур, выражаемых отрицательными числами на нетермодинамических Цельсия или же Шкала Фаренгейта, которые тем не менее выше, чем абсолютный ноль.

Шкалу абсолютной температуры (Кельвина) можно условно понять как меру средней кинетической энергии. Обычно температура системы положительная. Однако в отдельных изолированных системах температура определяется с помощью Энтропия Больцмана может стать отрицательным.

Возможность отрицательных температур впервые была предсказана Ларс Онсагер в 1949 г. при анализе классических точечных вихрей, ограниченных конечной площадью.^[1] Ограниченный точечные вихри представляют собой систему с ограниченным фазовым пространством, поскольку их канонические импульсы не являются независимыми степенями свободы от их канонических координат положения. Ограниченное фазовое пространство является существенным свойством, которое допускает отрицательные температуры, и такие температуры могут иметь место как в классических, так и в квантовых системах. Как показал Онсагер, система с ограниченным фазовым пространством обязательно имеет пик энтропии при увеличении энергии. Для энергий, превышающих значение, в котором возникает пик, энтропия уменьшается с увеличением энергии, и состояния с высокой энергией обязательно имеют отрицательную температуру Больцмана.

Система с действительно отрицательной температурой по шкале Кельвина горячее чем любая система с положительной температурой. Если система с отрицательной температурой и система с положительной температурой соприкасаются, тепло будет течь от системы с отрицательной температурой к системе с положительной температурой.^[2][3] Стандартный пример такой системы: инверсия населения в лазерная физика.

Температура в общих чертах интерпретируется как средняя кинетическая энергия частиц системы. Существование отрицательной температуры, не говоря уже об отрицательной температуре, представляющей «более горячие» системы, чем положительная температура, может показаться парадоксальным в этой интерпретации. Парадокс разрешается при рассмотрении более строгого определения понятия термодинамическая температура как компромисс между внутренняя энергия и энтропия содержится в системе, с "холодность ", взаимный температуры, являющейся более фундаментальной величиной. Системы с положительной температурой будут увеличивать энтропию по мере добавления энергии к системе, в то время как системы с отрицательной температурой будут уменьшаться в энтропии по мере добавления энергии к системе.^[4]

Термодинамические системы с неограниченным фазовое пространство невозможно достичь отрицательных температур: добавление высокая температура всегда увеличивает их энтропия. Возможность уменьшения энтропии с увеличением энергии требует, чтобы система «насыщалась» энтропией. Это возможно, только если количество состояний с высокой энергией ограничено. Для системы обычных (квантовых или классических) частиц, таких как атомы или пыль, количество состояний с высокой энергией неограниченно (импульсы частиц в принципе могут увеличиваться до бесконечности). Однако некоторые системы (см. Примеры ниже), имеют максимальное количество энергии, которое они могут удерживать, и по мере приближения к этой максимальной энергии их энтропия фактически начинает уменьшаться.^[5] Ограниченный диапазон состояний, доступных системе с отрицательной температурой, означает, что отрицательная температура связана с возникающим упорядочением системы при высоких энергиях. Например, в анализе точечных вихрей Онзагера отрицательная температура связана с появлением крупномасштабных скоплений вихрей.^[1] Это спонтанное упорядочение в статистической механике равновесия идет вразрез с общепринятой физической интуицией, согласно которой увеличение энергии ведет к усилению беспорядка.

Определение температуры

Определение термодинамическая температура Т является функцией изменения в системе энтропия S под обратимым теплопередача Q_rev:

${\displaystyle T={\frac {dQ_{\mathrm {rev} }}{dS}}.}$

Энтропия государственная функция, интеграл от dS над любым циклическим процессом равна нулю. Для системы, в которой энтропия является исключительно функцией энергии системы E, температуру можно определить как:

${\displaystyle T=\left({\frac {dS}{dE}}\right)^{-1}.}$

Эквивалентно термодинамическая бета, или «холодность», определяется как

${\displaystyle \beta ={\frac {1}{kT}}={\frac {1}{k}}{\frac {dS}{dE}},}$

куда k это Постоянная Больцмана.

Обратите внимание, что в классической термодинамике S определяется с точки зрения температуры. Здесь все наоборот, S это статистическая энтропия, функция возможных микросостояний системы, а температура передает информацию о распределении уровней энергии среди возможных микросостояний. Для систем со многими степенями свободы статистические и термодинамические определения энтропии обычно согласуются друг с другом.

Некоторые теоретики предложили использовать альтернативное определение энтропии как способ разрешения воспринимаемых несоответствий между статистической и термодинамической энтропией для небольших систем и систем, где количество состояний уменьшается с энергией, а температуры, полученные из этих энтропий, различны,^[6] хотя это новое определение привело бы к другим несоответствиям.^[7]

Распределение тепла и молекулярной энергии

Отрицательные температуры могут существовать только в системе с ограниченным числом энергетических состояний (см. Ниже). По мере увеличения температуры в такой системе частицы переходят в состояния с более высокой энергией, а при повышении температуры количество частиц в состояниях с более низкой энергией и в состояниях с более высокой энергией приближается к равенству. (Это следствие определения температуры в статистическая механика для систем с ограниченными состояниями). Вводя энергию в эти системы правильным образом, можно создать систему, в которой больше частиц в состояниях с более высокой энергией, чем в состояниях с более низкой энергией. В этом случае систему можно охарактеризовать как имеющую отрицательную температуру.

Вещество с отрицательной температурой не холоднее абсолютный ноль, а скорее она горячее, чем бесконечная температура. Как пишут Киттель и Кремер (стр. 462),

Шкала температур от холодного до горячего хода:

+0 K,…, +300 K,…, + ∞ K, −∞ K,…, −300 K,…, −0 K.

Соответствующая обратная шкала температур для величины β = 1/kT (куда k является Постоянная Больцмана ), непрерывно изменяется от низкой энергии к высокой при + ∞,…, 0,…, −∞. Поскольку он избегает резкого скачка от + ∞ до −∞, β считается более естественным, чем Т. Хотя система может иметь несколько областей с отрицательной температурой и, следовательно, иметь разрывы от −∞ до + ∞.

Во многих известных физических системах температура связана с кинетической энергией атомов. Поскольку нет верхней границы импульса атома, нет верхней границы количества энергетических состояний, доступных при добавлении дополнительной энергии, и, следовательно, нет способа достичь отрицательной температуры. Однако в статистической механике температура может соответствовать другим степеням свободы, кроме кинетической энергии (см. Ниже).

Температура и беспорядок

Распределение энергии между различными переводной, колебательный, вращающийся, электронный, и ядерный режимы системы определяет макроскопическую температуру. В «нормальной» системе происходит постоянный обмен тепловой энергией между различными режимами.

Однако в некоторых ситуациях можно выделить один или несколько режимов. На практике изолированные моды все еще обмениваются энергией с другими модами, но шкала времени этого обмена происходит намного медленнее, чем при обмене в изолированном режиме. Одним из примеров является случай ядерный спины в сильном внешнем магнитное поле. В этом случае энергия течет между спиновыми состояниями взаимодействующих атомов довольно быстро, но передача энергии между ядерными спинами и другими модами происходит относительно медленно. Поскольку поток энергии преимущественно находится внутри спиновой системы, имеет смысл думать о спиновой температуре, которая отличается от температуры, связанной с другими модами.

Определение температура может основываться на соотношении:

${\displaystyle T={\frac {dq_{\mathrm {rev} }}{dS}}}$

Отношения предполагают, что положительная температура соответствует условию где энтропия, S, увеличивается как тепловая энергия, q_rev, добавлен в систему. Это «нормальное» состояние в макроскопическом мире, и всегда так для поступательных, колебательных, вращательных и не связанных со спином электронных и ядерных мод. Причина в том, что есть бесконечный количество этих типов режимов, и добавление большего количества тепла к системе увеличивает количество режимов, которые являются энергетически доступными, и, таким образом, увеличивает энтропию.

Примеры

Невзаимодействующие двухуровневые частицы

Энтропия, термодинамическое бета и температура как функция энергии для системы N невзаимодействующие двухуровневые частицы.

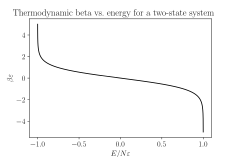
Самый простой пример, хотя и довольно нефизический, - это рассмотреть систему N частицы, каждая из которых может принимать энергию +ε или же −ε но в остальном они не взаимодействуют. Это можно понимать как предел Модель Изинга в котором член взаимодействия становится незначительным. Полная энергия системы

${\displaystyle E=\varepsilon \sum _{i=1}^{N}\sigma _{i}=\varepsilon j}$

куда σ_я это знак яth частица и j - количество частиц с положительной энергией минус количество частиц с отрицательная энергия. Из элементарного комбинаторика, общее количество микросостояния с таким количеством энергии биномиальный коэффициент:

${\displaystyle \Omega _{E}={\binom {N}{\frac {N+j}{2}}}={\frac {N!}{\left({\frac {N+j}{2}}\right)!\left({\frac {N-j}{2}}\right)!}}.}$

Посредством фундаментальное предположение статистической механики, энтропия этого микроканонический ансамбль является

${\displaystyle S=k_{\text{B}}\ln \Omega _{E}}$

Мы можем решить термодинамическую бета (β = 1/k_BТ), рассматривая его как центральная разница без перехода к континуальному пределу:

${\displaystyle {\begin{aligned}\beta &={\frac {1}{k_{\mathrm {B} }}}{\frac {\delta _{2\varepsilon }[S]}{2\varepsilon }}\\[3pt]&={\frac {1}{2\varepsilon }}\left(\ln \Omega _{E+\varepsilon }-\ln \Omega _{E-\varepsilon }\right)\\[3pt]&={\frac {1}{2\varepsilon }}\ln \left({\frac {\left({\frac {N+j-1}{2}}\right)!\left({\frac {N-j+1}{2}}\right)!}{\left({\frac {N+j+1}{2}}\right)!\left({\frac {N-j-1}{2}}\right)!}}\right)\\[3pt]&={\frac {1}{2\varepsilon }}\ln \left({\frac {N-j+1}{N+j+1}}\right).\end{aligned}}}$

следовательно, температура

${\displaystyle T(E)={\frac {2\varepsilon }{k_{\text{B}}}}\left[\ln \left({\frac {(N+1)\varepsilon -E}{(N+1)\varepsilon +E}}\right)\right]^{-1}.}$

Все это доказательство предполагает микроканонический ансамбль с фиксированной энергией и эмерджентным свойством температуры. в канонический ансамбль, температура фиксирована, а энергия является эмерджентным свойством. Это ведет к (ε относится к микросостояниям):

${\displaystyle {\begin{aligned}Z(T)&=\sum _{i=1}^{N}e^{-\varepsilon _{i}\beta }\\[6pt]E(T)&={\frac {1}{Z}}\sum _{i=1}^{N}\varepsilon _{i}e^{-\varepsilon _{i}\beta }\\[6pt]S(T)&=k_{\text{B}}\ln(Z)+{\frac {E}{T}}\end{aligned}}}$

Следуя предыдущему примеру, мы выбираем состояние с двумя уровнями и двумя частицами. Это приводит к микросостоянию ε₁ = 0, ε₂ = 1, ε₃ = 1, и ε₄ = 2.

${\displaystyle {\begin{aligned}Z(T)&=e^{-0\beta }+2e^{-1\beta }+e^{-2\beta }\\[3pt]&=1+2e^{-\beta }+e^{-2\beta }\\[6pt]E(T)&={\frac {0e^{-0\beta }+2\times 1e^{-1\beta }+2e^{-2\beta }}{Z}}\\[3pt]&={\frac {2e^{-\beta }+2e^{-2\beta }}{Z}}\\[3pt]&={\frac {2e^{-\beta }+2e^{-2\beta }}{1+2e^{-\beta }+e^{-2\beta }}}\\[6pt]S(T)&=k_{\text{B}}\ln \left(1+2e^{-\beta }+e^{-2\beta }\right)+{\frac {2e^{-\beta }+2e^{-2\beta }}{\left(1+2e^{-\beta }+e^{-2\beta }\right)T}}\end{aligned}}}$

Полученные значения для S, E, и Z все увеличивается с Т и никогда не нужно входить в отрицательный температурный режим.

Ядерные спины

Предыдущий пример приближенно реализуется системой ядерных спинов во внешнем магнитном поле.^[8][9] Это позволяет проводить эксперимент как вариант спектроскопия ядерного магнитного резонанса. В случае электронных и ядерных спиновых систем доступно лишь конечное число мод, часто всего две, соответствующих вращаться вверх и вниз. В отсутствие магнитное поле эти спиновые состояния выродиться, что означает, что они соответствуют одной и той же энергии. При приложении внешнего магнитного поля уровни энергии расщепляются, поскольку те спиновые состояния, которые выровнены с магнитным полем, будут иметь энергию, отличную от тех, которые антипараллельны ему.

В отсутствие магнитного поля такая двухспиновая система будет иметь максимальную энтропию, когда половина атомов находится в состоянии со спином вверх, а половина - в состоянии со спином вниз, и поэтому можно было бы ожидать найти систему с близким к равному распределению спинов. При приложении магнитного поля некоторые из атомов будут стремиться выровняться, чтобы минимизировать энергию системы, таким образом, немного больше атомов должно находиться в состоянии с более низкой энергией (для целей этого примера мы будем предполагать спин состояние down - это состояние с более низкой энергией). Можно добавить энергии к спиновой системе, используя радиочастота техники.^[10] Это заставляет атомы кувырок от замедления до раскрутки.

Поскольку мы начали с более чем половиной атомов в состоянии замедленного вращения, это сначала приводит систему к смеси 50/50, поэтому энтропия увеличивается, что соответствует положительной температуре. Однако в какой-то момент более половины спинов находятся в позиции раскрутки.^[11] В этом случае добавление дополнительной энергии снижает энтропию, так как это перемещает систему дальше от смеси 50/50. Это уменьшение энтропии с добавлением энергии соответствует отрицательной температуре.^[12] В ЯМР-спектроскопии это соответствует импульсам с шириной импульса более 180 ° (для данного спина). Хотя в твердых телах релаксация происходит быстро, в растворах она может длиться несколько секунд, а в газах и ультрахолодных системах - даже дольше; несколько часов были зарегистрированы для серебра и родия при пикокельвиновых температурах.^[12] По-прежнему важно понимать, что температура отрицательна только по отношению к ядерным спинам. Другие степени свободы, такие как молекулярные колебательные, электронные и спиновые уровни электронов, имеют положительную температуру, поэтому объект все еще имеет положительное физическое тепло. На самом деле релаксация происходит за счет обмена энергией между состояниями ядерного спина и другими состояниями (например, через ядерный эффект Оверхаузера с другими спинами).

Лазеры

Это явление также можно наблюдать во многих генерация системы, в которых большая часть атомы (для химических и газовых лазеров) или электроны (в полупроводник лазеры) находятся в возбужденном состоянии. Это называется инверсия населения.

В Гамильтониан для одиночной моды поля люминесцентного излучения на частоте ν является

${\displaystyle H=(h\nu -\mu )a^{\dagger }a.}$

Оператор плотности в большой канонический ансамбль является

${\displaystyle \rho ={\frac {e^{-\beta H}}{\operatorname {Tr} \left(e^{-\beta H}\right)}}.}$

Чтобы система имела основное состояние, след сходился и оператор плотности имел общий смысл, βH должно быть положительно полуопределенным. Так что если hν < μ, и ЧАС отрицательно полуопределено, то β сам по себе должен быть отрицательным, подразумевая отрицательную температуру.^[13]

Движущиеся степени свободы

Отрицательные температуры достигнуты и в двигательном степени свободы. Используя оптическая решетка, были поставлены ограничения на кинетическую энергию, энергию взаимодействия и потенциальную энергию холода. калий-39 атомы. Это было сделано путем настройки взаимодействия атомов с отталкивающего на притягивающее с помощью Резонанс Фешбаха и изменение общего гармонического потенциала с захвата на анти-захват, таким образом трансформируя Гамильтониан Бозе-Хаббарда из ЧАС → −ЧАС. Выполнение этого преобразования адиабатически при сохранении атомов в Изолятор Мотта В этом режиме можно перейти из состояния с низкой энтропией с положительной температурой в состояние с низкой энтропией с отрицательной температурой. В состоянии с отрицательной температурой атомы макроскопически занимают состояние решетки с максимальным импульсом. Ансамбли с отрицательной температурой уравновешиваются и показывают большие времена жизни в гармоническом потенциале, препятствующем захвату.^[14]

Двумерное вихревое движение

Двумерные системы вихрей, ограниченные конечной площадью, могут образовывать состояния теплового равновесия при состояниях с отрицательной температурой.,^[15][16] и действительно, состояния с отрицательной температурой были впервые предсказаны Онзагером в его анализе классических точечных вихрей.^[1] Предсказание Онзагера подтвердилось экспериментально для системы квантовые вихри в конденсате Бозе-Эйнштейна в 2019 г.^[17][18]

Смотрите также

• Абсолютно горячий
• Отрицательное сопротивление

Рекомендации

1. Онсагер, Л. (1949). «Статистическая гидродинамика». Il Nuovo Cimento. Nuovo Cim. 6 (Дополнение 2) (2): 279–287. Bibcode:1949NCim .... 6S.279O. Дои:10.1007 / BF02780991. ISSN  1827-6121. S2CID  186224016.
2. Рэмси, Норман (1956-07-01). «Термодинамика и статистическая механика при отрицательных абсолютных температурах». Физический обзор. 103 (1): 20–28. Bibcode:1956ПхРв..103 ... 20Р. Дои:10.1103 / PhysRev.103.20.
3. Трембле, Андре-Мари (1975-11-18). «Комментарий к: Отрицательные температуры по Кельвину: некоторые аномалии и предположения» (PDF). Американский журнал физики. 44 (10): 994–995. Bibcode:1976AmJPh..44..994T. Дои:10.1119/1.10248.
4. Аткинс, Питер В. (2010-03-25). Законы термодинамики: очень краткое введение. Издательство Оксфордского университета. С. 10–14. ISBN  978-0-19-957219-9. OCLC  467748903.
5. Аткинс, Питер В. (2010-03-25). Законы термодинамики: очень краткое введение. Издательство Оксфордского университета. С. 89–95. ISBN  978-0-19-957219-9. OCLC  467748903.
6. Дункель, Йорн; Гильберт, Стефан (2013). «Последовательная термостатистика запрещает отрицательные абсолютные температуры». Природа Физика. 10 (1): 67. arXiv:1304.2066. Bibcode:2014НатФ..10 ... 67Д. Дои:10.1038 / nphys2815. S2CID  16757018.
7. Френкель, Даан; Уоррен, Патрик Б. (01.02.2015). «Гиббс, Больцман и отрицательные температуры». Американский журнал физики. 83 (2): 163–170. arXiv:1403.4299. Bibcode:2015AmJPh..83..163F. Дои:10.1119/1.4895828. ISSN  0002-9505. S2CID  119179342.
8. Перселл, Э.; Паунд, Р.В. (1951-01-15). «Ядерная спиновая система при отрицательной температуре». Физический обзор. 81 (2): 279–280. Bibcode:1951ПхРв ... 81..279П. Дои:10.1103 / PhysRev.81.279.
9. Варга, Питер (1998). «Минимаксные игры, спиновые очки и иерархия классов сложности с полиномиальным временем». Физический обзор E. 57 (6): 6487–6492. arXiv:cond-mat / 9604030. Bibcode:1998PhRvE..57.6487V. CiteSeerX  10.1.1.306.470. Дои:10.1103 / PhysRevE.57.6487. S2CID  10964509.
10. Рэмси, Норман Ф. (1998). Спектроскопия с когерентным излучением: избранные статьи Нормана Ф. Рэмси с комментариями. Всемирная научная серия по физике 20 века, т. 21. Сингапур; Ривер Эдж, Нью-Джерси: World Scientific. п. 417. ISBN  9789810232504. OCLC  38753008.
11. Левитт, Малкольм Х. (2008). Спиновая динамика: основы ядерного магнитного резонанса. Западный Суссекс, Англия: John Wiley & Sons Ltd. стр. 273. ISBN  978-0-470-51117-6.
12. «Положительные и отрицательные пикокельвиновые температуры».
13. Hsu, W .; Баракат, Р. (1992). «Статистика и термодинамика люминесцентного излучения». Физический обзор B. 46 (11): 6760–6767. Bibcode:1992PhRvB..46.6760H. Дои:10.1103 / PhysRevB.46.6760. PMID  10002377.
14. Braun, S .; Ronzheimer, J. P .; Schreiber, M .; Hodgman, S. S .; Rom, T .; Bloch, I .; Шнайдер, У. (2013). «Отрицательная абсолютная температура для двигательных степеней свободы». Наука. 339 (6115): 52–55. arXiv:1211.0545. Bibcode:2013Наука ... 339 ... 52Б. Дои:10.1126 / science.1227831. PMID  23288533. S2CID  8207974.
15. Монтгомери, Д. К. (1972). «Двумерное вихревое движение и» отрицательные температуры."". Письма о физике A. 39 (1): 7–8. Bibcode:1972ФЛА ... 39 .... 7М. Дои:10.1016/0375-9601(72)90302-7.
16. Эдвардс, С.Ф.; Тейлор, Дж. Б. (1974). «Отрицательные температурные состояния двумерной плазмы и вихревой жидкости». Труды Лондонского королевского общества A. 336 (1606): 257–271. Bibcode:1974RSPSA.336..257E. Дои:10.1098 / RSPA.1974.0018. JSTOR  78450. S2CID  120771020.
17. Gauthier, G .; Ривз, М. Т .; Yu, X .; Брэдли, А. С .; Бейкер, М. А .; Bell, T. A .; Rubinsztein-Dunlop, H .; Дэвис, М. Дж .; Нили, Т. У. (2019). «Гигантские вихревые скопления в двумерной квантовой жидкости». Наука. 364 (6447): 1264–1267. arXiv:1801.06951. Bibcode:2019Научный ... 364.1264G. Дои:10.1126 / science.aat5718. PMID  31249054. S2CID  195750381.
18. Johnstone, S.P .; Groszek, A.J .; Старки, П. Т .; Billinton, C.J .; Simula, T. P .; Хелмерсон, К. (2019). «Эволюция крупномасштабного потока из турбулентности в двумерной сверхтекучей жидкости». Наука. 365 (6447): 1267–1271. arXiv:1801.06952. Bibcode:2019Научный ... 364.1267J. Дои:10.1126 / science.aat5793. PMID  31249055. S2CID  4948239.

дальнейшее чтение

• Киттель, К.; Кремер, Х. (1980). Теплофизика (2-е изд.). В. Х. Фриман. ISBN  978-0-7167-1088-2.
• Castle, J .; Emmerich, W .; Heikes, R .; Miller, R .; Рейн, Дж. (1965). Наука по степеням: Температура от нуля до нуля. Уокер и компания. LCCN  64023985.
• Braun, S .; Ronzheimer, J. P .; Schreiber, M .; Hodgman, S. S .; Rom, T .; Bloch, I .; Шнайдер, У. (2013). «Отрицательная абсолютная температура для двигательных степеней свободы». Наука. 339 (6115): 52–5. arXiv:1211.0545. Bibcode:2013Наука ... 339 ... 52Б. Дои:10.1126 / science.1227831. PMID  23288533. S2CID  8207974.
• Parihar, V .; Widom, A .; Шривастава Ю. (2006). «Температурные шкалы времени в цветном стеклянном конденсате». Физический обзор C. 73 (17901): 017901. arXiv:hep-ph / 0505199. Bibcode:2006PhRvC..73a7901P. Дои:10.1103 / PhysRevC.73.017901. S2CID  119090586.
• Моск, А. (2005). «Атомарные газы при отрицательной кинетической температуре». Письма с физическими проверками. 95 (4): 040403. arXiv:cond-mat / 0501344. Bibcode:2005ПхРвЛ..95д0403М. Дои:10.1103 / PhysRevLett.95.040403. PMID  16090784. S2CID  1156732.
• Шмидт, Гарри; Малер, Гюнтер (2005). «Управление локальным релаксационным поведением в замкнутых двудольных квантовых системах». Физический обзор E. 72 (7): 016117. arXiv:Quant-ph / 0502181. Bibcode:2005PhRvE..72a6117S. Дои:10.1103 / PhysRevE.72.016117. PMID  16090046. S2CID  17987338.
• Шен, Цзянь-Ци (2003). «Эффект защиты от экранирования и отрицательная температура в мгновенно инвертированных электрических полях и левосторонних средах». Physica Scripta. 68 (1): 87–97. arXiv:cond-mat / 0302351. Bibcode:2003 ФОТО ... 68 ... 87S. Дои:10.1238 / Physica.Regular.068a00087. S2CID  118894011.
• Кеттерле, Вольфганг (22 сентября 2010 г.). К квантовому магнетизму с ультрахолодными атомами (фильм). Коллоквиум по физике в Цюрихе. ETH Zurich, ITS-MMS; Швейцария. Получено 1 января 2016. Отрицательная температура, около 48 мин. 53сек.
• Карр, Линкольн Д. (4 января 2013 г.). «Отрицательные температуры?». Наука. 339 (6115): 42–43. Bibcode:2013Наука ... 339 ... 42C. Дои:10.1126 / science.1232558. PMID  23288530. S2CID  124095369.

внешняя ссылка

• Мориарти, Филипп. «−K: отрицательные температуры». Шестьдесят символов. Брэди Харан для Ноттингемский университет.