Алгоритм цепочки ближайшего соседа - Nearest-neighbor chain algorithm

В теории кластерный анализ, то алгоритм цепочки ближайших соседей является алгоритм это может ускорить несколько методов для агломеративная иерархическая кластеризация. Это методы, которые принимают набор точек в качестве входных данных и создают иерархию кластеров точек путем многократного слияния пар меньших кластеров для формирования более крупных кластеров. Методы кластеризации, для которых может использоваться алгоритм цепочки ближайших соседей, включают Метод Уорда, кластеризация с полной связью, и одинарная кластеризация; все они работают путем многократного слияния двух ближайших кластеров, но используют разные определения расстояния между кластерами. Кластерные расстояния, для которых работает алгоритм цепочки ближайших соседей, называются сводимый и характеризуются простым неравенством между определенными расстояниями между кластерами.

Основная идея алгоритма - найти пары кластеров для слияния, следуя пути в граф ближайшего соседа кластеров. Каждый такой путь в конечном итоге заканчивается парой кластеров, которые являются ближайшими соседями друг друга, и алгоритм выбирает эту пару кластеров в качестве пары для слияния. Чтобы сэкономить работу за счет повторного использования как можно большего количества каждого пути, алгоритм использует структура данных стека чтобы отслеживать каждый путь, по которому он следует. Следуя таким путем, алгоритм цепочки ближайших соседей объединяет свои кластеры в порядке, отличном от порядка методов, которые всегда находят и объединяют ближайшую пару кластеров. Однако, несмотря на эту разницу, он всегда генерирует одну и ту же иерархию кластеров.

Алгоритм цепочки ближайших соседей строит кластеризацию по времени, пропорциональному квадрату количества точек, которые должны быть кластеризованы. Это также пропорционально размеру его ввода, когда ввод предоставляется в форме явного матрица расстояний. Алгоритм использует объем памяти, пропорциональный количеству точек, когда он используется для методов кластеризации, таких как метод Уорда, который позволяет вычислять расстояние между кластерами в постоянное время. Однако для некоторых других методов кластеризации он использует больший объем памяти во вспомогательной структуре данных, с помощью которой он отслеживает расстояния между парами кластеров.

Фон

Иерархическая кластеризация из шести точек. Точки для кластеризации находятся в верхней части диаграммы, а узлы под ними представляют кластеры.

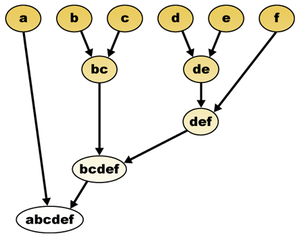
Много проблем в анализ данных беспокойство кластеризация, группируя элементы данных в кластеры тесно связанных элементов. Иерархическая кластеризация - это версия кластерного анализа, в которой кластеры образуют иерархию или древовидную структуру, а не строгое разделение элементов данных. В некоторых случаях этот тип кластеризации может выполняться как способ выполнения кластерного анализа одновременно в нескольких различных масштабах. В других случаях анализируемые данные естественным образом имеют неизвестную древовидную структуру, и цель состоит в том, чтобы восстановить эту структуру путем выполнения анализа. Оба эти вида анализа можно увидеть, например, в применении иерархической кластеризации к биологическая таксономия. В этом приложении разные живые существа сгруппированы в кластеры на разных уровнях или уровнях сходства (вид, род, семейство и т. д. ). Этот анализ одновременно дает многомасштабную группировку организмов современной эпохи и направлен на точную реконструкцию процесса ветвления или эволюционное дерево что в прошлые века производили эти организмы.^[1]

Вход в задачу кластеризации состоит из набора точек.^[2] А кластер - любое собственное подмножество точек, а иерархическая кластеризация - это максимальный семейство кластеров со свойством, что любые два кластера в семействе либо вложены, либо непересекающийся В качестве альтернативы иерархическая кластеризация может быть представлена ​​как двоичное дерево острием на его листьях; кластеры кластеризации - это наборы точек в поддеревьях, спускающиеся от каждого узла дерева.^[3]

В методах агломерационной кластеризации входные данные также включают функцию расстояния, определенную для точек, или числовую меру их несходства. Расстояние или несходство должны быть симметричными: расстояние между двумя точками не зависит от того, какая из них считается первой. , в отличие от расстояний в метрическое пространство, не требуется неравенство треугольника.^[2]Затем функция несходства расширяется с пар точек на пары кластеров. Различные методы кластеризации выполняют это расширение по-разному. Например, в одинарная кластеризация , расстояние между двумя кластерами определяется как минимальное расстояние между любыми двумя точками из каждого кластера. Учитывая это расстояние между кластерами, иерархическая кластеризация может быть определена жадный алгоритм который изначально помещает каждую точку в свой собственный одноточечный кластер, а затем многократно формирует новый кластер путем слияния ближайшая пара кластеров.^[2]

Узким местом этого жадного алгоритма является подзадача поиска, какие два кластера следует объединить на каждом шаге. Известные методы многократного поиска ближайшей пары кластеров в динамическом наборе кластеров либо требуют сверхлинейного пространства для поддержания структура данных которые могут быстро найти ближайшие пары, или им требуется больше, чем линейное время, чтобы найти каждую ближайшую пару.^[4][5] Алгоритм цепочки ближайших соседей использует меньше времени и пространства, чем жадный алгоритм, объединяя пары кластеров в другом порядке. Таким образом, устраняется проблема многократного поиска ближайших пар. Тем не менее, для многих типов проблем кластеризации можно гарантированно получить ту же иерархическую кластеризацию, что и жадный алгоритм, несмотря на другой порядок слияния.^[2]

Алгоритм

Анимация алгоритма с использованием расстояния Уорда. Черные точки - это точки, серые области - это большие кластеры, синие стрелки указывают на ближайших соседей, а красная полоса указывает на текущую цепочку. Для визуальной простоты, когда слияние оставляет цепочку пустой, она продолжается с недавно объединенным кластером.

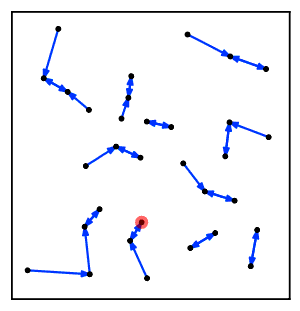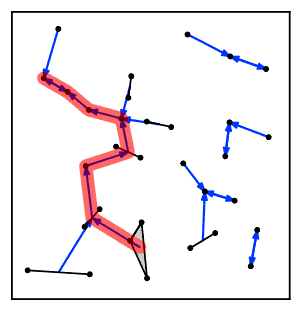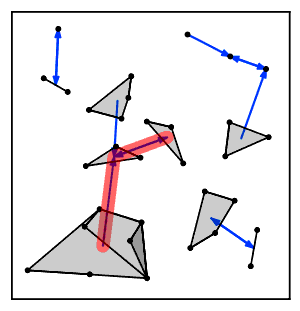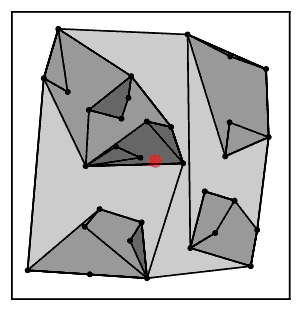
Интуитивно понятно, что алгоритм цепочки ближайших соседей постоянно следует цепочке кластеров. А → B → C → ... где каждый кластер является ближайшим соседом предыдущего, пока не достигнет пары кластеров, которые являются взаимными ближайшими соседями.^[2]

Более подробно алгоритм выполняет следующие шаги:^[2][6]

• Инициализировать набор активных кластеров, чтобы он состоял из п одноточечные кластеры, по одному на каждую входную точку.
• Позволять S быть структура данных стека, изначально пустые, элементы которых будут активными кластерами.
• Пока в наборе кластеров более одного кластера:
  • Если S пусто, выберите произвольно активный кластер и поместите его на S.
  • Позволять C быть активным кластером на вершине S. Вычислить расстояния от C ко всем остальным кластерам, и пусть D быть ближайшим другим кластером.
  • Если D уже в S, он должен быть непосредственным предшественником C. Вытащить оба кластера из S и объединить их.
  • В противном случае, если D еще не в S, надавите на S.

Когда у одного кластера может быть несколько равных ближайших соседей, алгоритм требует согласованного правила разрыва связи. Например, можно присвоить произвольные порядковые номера всем кластерам, а затем выбрать (среди равных ближайших соседей) тот, у которого наименьший порядковый номер. Это правило предотвращает определенные виды несогласованного поведения в алгоритме; например, без такого правила соседний кластер D может появиться в стеке раньше, чем предшественник C.^[7]

Анализ времени и пространства

Каждая итерация цикла выполняет одиночный поиск ближайшего соседа кластера и либо добавляет один кластер в стек, либо удаляет из него два кластера. Каждый кластер добавляется в стек только один раз, потому что при повторном удалении он немедленно становится неактивным и объединяется. Всего есть 2п − 2 кластеры, которые когда-либо добавляются в стек: п одноточечные кластеры в исходном наборе, и п − 2 внутренние узлы, отличные от корня в двоичном дереве, представляющем кластеризацию. Следовательно, алгоритм выполняет 2п − 2 продвижение итераций и п − 1 выскакивают итерации.^[2]

Каждая из этих итераций может тратить время на сканирование до п − 1 расстояние между кластерами, чтобы найти ближайшего соседа, поэтому общее количество вычислений расстояния, которое он выполняет, меньше, чем 3п²По той же причине общее время, используемое алгоритмом вне этих вычислений расстояния, равно O (п²).^[2]

Поскольку единственной структурой данных является набор активных кластеров и стек, содержащий подмножество активных кластеров, требуемое пространство линейно зависит от количества входных точек.^[2]

Правильность

Чтобы алгоритм был правильным, это должно быть так, что выталкивание и объединение двух верхних кластеров из стека алгоритма сохраняет свойство, состоящее в том, что остальные кластеры в стеке образуют цепочку ближайших соседей. кластеров, созданных в ходе алгоритма, такие же, как кластеры, созданные жадный алгоритм который всегда объединяет два ближайших кластера, даже несмотря на то, что жадный алгоритм обычно выполняет свои объединения в другом порядке, чем алгоритм цепочки ближайших соседей. Оба эти свойства зависят от конкретного выбора способа измерения расстояния между кластерами.^[2]

Правильность этого алгоритма зависит от свойства его функции расстояния, называемой сводимость. Это свойство было идентифицировано Bruynooghe (1977) в связи с более ранним методом кластеризации, который использовал взаимные пары ближайших соседей, но не цепочки ближайших соседей.^[8] Функция расстояния d на кластерах определяется как приводимый, если для каждых трех кластеров А, B и C в жадной иерархической кластеризации, такой что А и B являются взаимными ближайшими соседями, выполняется неравенство:^[2]

d(А ∪ B, C) ≥ min (d (А,C), d (B,C)).

Если функция расстояния имеет свойство сводимости, то слияние двух кластеров C и D может вызвать только ближайшего соседа E изменить, если ближайший сосед был одним из C и D. Это имеет два важных последствия для алгоритма цепочки ближайших соседей. Во-первых, с помощью этого свойства можно показать, что на каждом шаге алгоритма кластеры в стеке S формируют действительную цепочку ближайших соседей, потому что всякий раз, когда ближайший сосед становится недействительным, он немедленно удаляется из стека.^[2]

Во-вторых, что еще более важно, из этого свойства следует, что если два кластера C и D оба принадлежат к жадной иерархической кластеризации и являются взаимными ближайшими соседями в любой момент времени, тогда они будут объединены жадной кластеризацией, поскольку они должны оставаться взаимными ближайшими соседями до тех пор, пока не будут объединены. Отсюда следует, что каждая пара взаимных ближайших соседей, найденная алгоритмом цепочки ближайших соседей, также является парой кластеров, найденных жадным алгоритмом, и, следовательно, алгоритм цепочки ближайших соседей вычисляет точно такую ​​же кластеризацию (хотя и в другом порядке), что и жадный алгоритм. алгоритм.^[2]

Применение к определенным расстояниям кластеризации

Метод Уорда

Метод Уорда представляет собой метод агломерационной кластеризации, в котором различие между двумя кластерами А и B измеряется количеством, на которое слияние двух кластеров в один больший кластер увеличит средний квадрат расстояния от точки до этого кластера. центроид.^[9] То есть,

${\displaystyle d(A,B)=\sum _{x\in A,y\in B}{\frac {d^{2}(x,y)}{|A|+|B|}}-\sum _{x,y\in A}{\frac {d^{2}(x,y)}{|A|}}-\sum _{x,y\in B}{\frac {d^{2}(x,y)}{|B|}}.}$

Выражается через центроид ${\displaystyle c_{A}}$ и мощность ${\displaystyle n_{A}}$ из двух кластеров он имеет более простую формулу

${\displaystyle d(A,B)={\frac {d^{2}(c_{a},c_{b})}{1/n_{A}+1/n_{B}}},}$

что позволяет рассчитывать его за постоянное время на расчет расстояния. выбросы, Метод Уорда является наиболее популярным вариантом агломеративной кластеризации как из-за круглой формы кластеров, которые он обычно формирует, так и из-за его принципиального определения как кластеризации, которая на каждом этапе имеет наименьшую дисперсию в своих кластерах.^[10] В качестве альтернативы это расстояние можно рассматривать как разницу в k-означает стоимость между новым кластером и двумя старыми кластерами.

Расстояние Уорда также можно уменьшить, что легче увидеть из другой формулы для расчета расстояния объединенного кластера на основе расстояний кластеров, из которых он был объединен:^[9][11]

${\displaystyle d(A\cup B,C)={\frac {n_{A}+n_{C}}{n_{A}+n_{B}+n_{C}}}d(A,C)+{\frac {n_{B}+n_{C}}{n_{A}+n_{B}+n_{C}}}d(B,C)-{\frac {n_{C}}{n_{A}+n_{B}+n_{C}}}d(A,B).}$

Формулы обновления расстояний, подобные этой, называются формулами «типа Ланса – Вильямса» после работы Лэнс и Уильямс (1967).Если ${\displaystyle d(A,B)}$ - наименьшее из трех расстояний в правой части (что обязательно будет верно, если ${\displaystyle A}$ и ${\displaystyle B}$ являются взаимными ближайшими соседями), то отрицательный вклад от его члена компенсируется ${\displaystyle n_{C}}$ коэффициент одного из двух других членов, оставляя положительное значение, добавленное к средневзвешенному значению двух других расстояний. Следовательно, суммарное расстояние всегда не меньше минимального ${\displaystyle d(A,C)}$ и ${\displaystyle d(B,C)}$, отвечающее определению сводимости.

Поскольку расстояние Уорда можно уменьшить, алгоритм цепочки ближайших соседей, использующий расстояние Уорда, вычисляет точно такую ​​же кластеризацию, как и стандартный жадный алгоритм. За п очков в Евклидово пространство постоянного размера, требуется время О(п²) и космос О(п).^[6]

Полная навеска и среднее расстояние

Полная связь или кластеризация по наиболее дальним соседям - это форма агломеративной кластеризации, которая определяет несходство между кластерами как максимальное расстояние между любыми двумя точками из двух кластеров. Точно так же кластеризация среднего расстояния использует среднее попарное расстояние в качестве несходства. Как и расстояние Уорда, эти две формы кластеризации подчиняются формуле типа Ланса – Вильямса. При полной сцепке расстояние ${\displaystyle d(A\cup B,C)}$ это максимальное из двух расстояний ${\displaystyle d(A,C)}$ и ${\displaystyle d(B,C)}$. Следовательно, оно, по крайней мере, равно минимуму из этих двух расстояний, что является требованием для уменьшения. Для среднего расстояния ${\displaystyle d(A\cup B,C)}$ это просто средневзвешенное значение расстояний ${\displaystyle d(A,C)}$ и ${\displaystyle d(B,C)}$. Опять же, это, по крайней мере, равно минимальному из двух расстояний. Таким образом, в обоих случаях расстояние можно уменьшить.^[9][11]

В отличие от метода Уорда, эти две формы кластеризации не имеют метода постоянного времени для вычисления расстояний между парами кластеров. Вместо этого можно поддерживать массив расстояний между всеми парами кластеров. Всякий раз, когда два кластера объединяются, формула может использоваться для вычисления расстояния между объединенным кластером и всеми другими кластерами. Поддержание этого массива в ходе алгоритма кластеризации требует времени и места. О(п²). Алгоритм цепочки ближайших соседей может использоваться в сочетании с этим массивом расстояний, чтобы найти ту же кластеризацию, что и жадный алгоритм для этих случаев. Его общее время и пространство, используя этот массив, также О(п²).^[12]

Такой же О(п²) временные и пространственные границы также могут быть достигнуты другим способом, с помощью техники, которая накладывает квадродерево -основанная структура данных очереди приоритетов поверх матрицы расстояний и использует ее для выполнения стандартного жадного алгоритма кластеризации. Этот метод квадродерева является более общим, так как он работает даже для методов кластеризации, которые не сводятся.^[4] Однако алгоритм цепочки ближайших соседей соответствует своим временным и пространственным ограничениям при использовании более простых структур данных.^[12]

Одиночная связь

В одинарная связь или кластеризация ближайшего соседа, самая старая форма агломеративной иерархической кластеризации,^[11] несходство между кластерами измеряется как минимальное расстояние между любыми двумя точками из двух кластеров. С этой непохожестью,

${\displaystyle d(A\cup B,C)=\min(d(A,C),d(B,C)),}$

удовлетворение как равенство, а не как неравенство требованию сводимости. (Одинарное соединение также подчиняется формуле Ланса – Вильямса,^[9][11] но с отрицательным коэффициентом, из которого труднее доказать сводимость.)

Как и в случае с полной связью и средним расстоянием, сложность вычисления кластерных расстояний заставляет алгоритм цепочки ближайших соседей занимать время и пространство. О(п²) для вычисления кластеризации с одной связью. Однако кластеризацию с одной связью можно найти более эффективно с помощью альтернативного алгоритма, который вычисляет минимальное остовное дерево входных расстояний с использованием Алгоритм Прима, а затем сортирует минимальные границы остовного дерева и использует этот отсортированный список для управления слиянием пар кластеров. В алгоритме Прима каждое последующее минимальное ребро остовного дерева можно найти с помощью последовательный поиск через несортированный список наименьших ребер, соединяющих частично построенное дерево с каждой дополнительной вершиной. Этот выбор экономит время, которое в противном случае алгоритм потратил бы на настройку весов вершин в своем приоритетная очередь. Использование алгоритма Прима таким образом потребует времени О(п²) и космос О(п), сопоставление наилучших границ, которые могут быть достигнуты с помощью алгоритма цепочки ближайших соседей для расстояний с расчетами с постоянным временем.^[13]

Центроидное расстояние

Другая мера расстояния, обычно используемая в агломеративной кластеризации, - это расстояние между центроидами пар кластеров, также известное как метод взвешенных групп.^[9][11] Его можно легко рассчитать за постоянное время для расчета расстояния. Однако это не сводится. Например, если входные данные образуют набор из трех точек равностороннего треугольника, объединение двух из этих точек в больший кластер приводит к уменьшению межкластерного расстояния, нарушению сводимости. Следовательно, алгоритм цепочки ближайших соседей не обязательно найдет ту же кластеризацию, что и жадный алгоритм. Тем не менее, Муртаг (1983) пишет, что алгоритм цепочки ближайших соседей обеспечивает "хорошую эвристику" для метода центроидов.^[2]Другой алгоритм Дэй и Эдельсбруннер (1984) можно использовать для поиска жадной кластеризации в О(п²) время для измерения расстояния.^[5]

Расстояния, чувствительные к порядку слияния

В приведенной выше презентации явно запрещены расстояния, чувствительные к порядку слияния. Действительно, разрешение на такие расстояния может вызвать проблемы. В частности, существуют чувствительные к порядку кластерные расстояния, которые удовлетворяют сводимости, но для которых вышеупомянутый алгоритм вернет иерархию с субоптимальными затратами. Следовательно, когда расстояния между кластерами определяются рекурсивной формулой (как некоторые из рассмотренных выше), следует позаботиться о том, чтобы они не использовали иерархию таким образом, который чувствителен к порядку слияния.^[14]

История

Алгоритм цепочки ближайших соседей был разработан и реализован в 1982 г. Жан-Поль Бензекри^[15] и Дж. Хуан.^[16] Они основали этот алгоритм на более ранних методах, которые строили иерархические кластеры с использованием взаимных пар ближайших соседей без использования цепочек ближайших соседей.^[8][17]

Рекомендации

1. Гордон, Аллан Д. (1996), «Иерархическая кластеризация», в Arabie, P .; Hubert, L.J .; Де Соэте, Г. (ред.), Кластеризация и классификация, Ривер Эдж, штат Нью-Джерси: World Scientific, стр. 65–121, ISBN  9789814504539.
2. Муртаг, Фионн (1983), «Обзор последних достижений в алгоритмах иерархической кластеризации» (PDF), Компьютерный журнал, 26 (4): 354–359, Дои:10.1093 / comjnl / 26.4.354.
3. Сюй, Руи; Вунш, Дон (2008), «3.1 Иерархическая кластеризация: введение», Кластеризация, Серия изданий IEEE по вычислительному интеллекту, 10, John Wiley & Sons, стр. 31, ISBN  978-0-470-38278-3.
4. Эппштейн, Дэвид (2000), «Быстрая иерархическая кластеризация и другие приложения динамических ближайших пар», J. Экспериментальная алгоритмика, ACM, 5 (1): 1–23, arXiv:cs.DS / 9912014, Bibcode:1999cs ....... 12014E.
5. Дэй, Уильям Х. Э .; Эдельсбруннер, Герберт (1984), «Эффективные алгоритмы методов агломеративной иерархической кластеризации» (PDF), Журнал классификации, 1 (1): 7–24, Дои:10.1007 / BF01890115.
6. Муртаг, Фионн (2002), «Кластеризация в массивных наборах данных», в Abello, James M .; Pardalos, Panos M .; Ресенде, Маурисио Г. К. (ред.), Справочник массивных наборов данных, Массовые вычисления, 4, Springer, стр. 513–516, Bibcode:2002hmds.book ..... A, ISBN  978-1-4020-0489-6.
7. Для этого правила разрыва связи и примера того, как нарушение связи необходимо для предотвращения циклов в графе ближайшего соседа, см. Седжвик, Роберт (2004), «Рисунок 20.7», Алгоритмы в Java, часть 5: Графические алгоритмы (3-е изд.), Addison-Wesley, p. 244, ISBN  0-201-36121-3.
8. Bruynooghe, Мишель (1977), "Méthodes Nouvelles en Classification Automatique de Données taxinomiqes nombreuses", Statistique et Analyze des Données, 3: 24–42.
9. Миркин, Борис (1996), Математическая классификация и кластеризация, Невыпуклая оптимизация и ее приложения, 11, Dordrecht: Kluwer Academic Publishers, стр. 140–144, ISBN  0-7923-4159-7, МИСТЕР  1480413.
10. Таффери, Стефан (2011), «9.10 Агломеративная иерархическая кластеризация», Интеллектуальный анализ данных и статистика для принятия решений, Серия Уайли по вычислительной статистике, стр. 253–261, ISBN  978-0-470-68829-8.
11. Lance, G.N .; Уильямс, В. Т. (1967), "Общая теория классификационных стратегий сортировки. I. Иерархические системы", Компьютерный журнал, 9 (4): 373–380, Дои:10.1093 / comjnl / 9.4.373.
12. Гронау, Илан; Моран, Шломо (2007), «Оптимальные реализации UPGMA и других распространенных алгоритмов кластеризации», Письма об обработке информации, 104 (6): 205–210, Дои:10.1016 / j.ipl.2007.07.002, МИСТЕР  2353367.
13. Gower, J.C .; Росс, Дж. Дж. С. (1969), "Минимальные остовные деревья и кластерный анализ единственной связи", Журнал Королевского статистического общества, серия C, 18 (1): 54–64, JSTOR  2346439, МИСТЕР  0242315.
14. Мюлльнер, Даниэль (2011), Современные иерархические агломеративные алгоритмы кластеризации, 1109, arXiv:1109.2378, Bibcode:2011arXiv1109.2378M.
15. Benzécri, J.-P. (1982), "Construction d'une классификации ascendante hiérarchique par la recherche en chaîne des voisins réciproques", Les Cahiers de l'Analyse des Données, 7 (2): 209–218.
16. Хуан, Дж. (1982), "Программа иерархической классификации по алгоритму поиска в цепочке обратных звуков", Les Cahiers de l'Analyse des Données, 7 (2): 219–225.
17. де Рам, К. (1980), "La Classification hiérarchique ascendante selon la méthode des voisins réciproques", Les Cahiers de l'Analyse des Données, 5 (2): 135–144.