Московский математический папирус - Moscow Mathematical Papyrus

Московский математический папирус
Московский математический папирус
	Государственный музей изобразительных искусств имени А.С. Пушкина в Москве
	14-я проблема Московского математического папируса (В. Струве, 1930)
Дата	13 династия, Второй промежуточный период Египта
Место происхождения	Фивы
Язык (и)	Иератический
Размер	Длина: 5,5 метра (18 футов); Ширина: от 3,8 до 7,6 см (от 1,5 до 3 дюймов)

В Московский математический папирус это древний Египетская математика папирус, также называемый Математический папирус Голенищевапосле первого владельца за пределами Египта, египтолог Владимир Голенищев. Голенищев купил папирус в 1892 или 1893 году в г. Фивы. Позже он вошел в коллекцию Государственный музей изобразительных искусств имени А.С. Пушкина в Москве, где и остается сегодня.

На основе палеография и орфография иератический текст, скорее всего, текст был записан в 13-я династия и основан на более старых материалах, вероятно, относящихся к Двенадцатая династия Египта, примерно 1850 г. до н.э.^[1] Приблизительно 5½ м (18 футов) в длину и от 3,8 до 7,6 см (1,5 и 3 дюйма) в ширину, его формат был разделен на 25 задач с решениями Советский Востоковед Василий Васильевич Струве^[2] в 1930 г.^[3] Это хорошо известный математический папирус, на который обычно ссылаются Математический папирус Райнда. Математический папирус Москвы старше Математического папируса Райнда, в то время как последний является большим из двух.^[4]

Упражнения из Московского папируса

Задачи в Московском папирусе не следуют определенному порядку, и решения проблем содержат гораздо меньше деталей, чем в Математический папирус Райнда. Папирус хорошо известен своими геометрическими проблемами. В задачах 10 и 14 вычисляются площадь поверхности и объем усеченный соответственно. Остальные проблемы имеют более общий характер.^[1]

Проблемы с судовой частью

Проблемы 2 и 3 относятся к частям корабля. Одна из задач вычисляет длину судового руля, а другая вычисляет длину судовой мачты, учитывая, что она составляет 1/3 + 1/5 длины кедрового бревна первоначально 30. локти длинный.^[1]

Ага проблемы

Ага
в иероглифы

Проблемы Aha включают поиск неизвестных величин (называемых Aha), если даны сумма количества и части (ей). В Математический папирус Райнда также содержит четыре таких типа проблем. Проблемы 1, 19 и 25 Московского папируса - это проблемы Ага. Например, в задаче 19 предлагается вычислить количество, взятое 1 и ½ раза и добавленное к 4, чтобы получить 10.^[1] Другими словами, в современных математических обозначениях просят решить ${ displaystyle { frac {3} {2}} x + 4 = 10}$ .

Проблемы Pefsu

Большинство проблем связаны с проблемами pefsu (см .: Египетская алгебра ): 10 из 25 задач. Pefsu измеряет крепость пива, приготовленного из гекат зерна

{ displaystyle { mbox {pefsu}} = { frac { mbox {количество буханок хлеба (или кувшинов пива)}} { mbox {количество геков зерна}}}}

Более высокое число pefsu означает более слабый хлеб или пиво. Номер pefsu упоминается во многих списках предложений. Например, проблема 8 переводится как:

(1) Пример расчета 100 буханок хлеба пефсу 20

(2) Если кто-то говорит вам: «У вас есть 100 хлебов пефсу 20

(3) обменять на пиво пефсу 4

(4) как 1/2 1/4 солодового финикового пива "

(5) Сначала рассчитайте зерно, необходимое для 100 буханок хлеба пефсу 20.

(6) Результат 5 хекат. Затем посчитайте, что вам нужно для дес-кувшина пива, например, пива под названием 1/2 1/4 солодового финикового пива.

(7) В результате получается 1/2 доли heqat, необходимой для удаления кувшина пива из верхнеегипетского зерна.

(8) Вычислите 1/2 от 5 гекатов, результат будет 2 1/2.

(9) Возьмите это 2 1/2 четыре раза

(10) Результат - 10. Затем вы говорите ему:

(11) «Вот! Количество пива определено правильно».^[1]

Бакинские проблемы

Проблемы 11 и 23 - проблемы Баку. Они подсчитывают выпуск рабочих. Задача 11 спрашивает, если кто-то принесет 100 бревен размером 5 на 5, то сколько бревен размером 4 на 4 это соответствует? Задача 23 связана с производством сапожника, учитывая, что он должен вырезать и украсить сандалии.^[1]

Проблемы геометрии

Семь из двадцати пяти задач являются задачами геометрии и варьируются от вычисления площадей треугольников до определения площади поверхности полусферы (задача 10) и определения объема усеченный (усеченная пирамида).^[1]

Две проблемы геометрии

Проблема 10

Десятая задача Московского математического папируса требует вычисления площади поверхности полушарие (Струве, Жиллингс) или, возможно, площадь полуцилиндра (Пит). Ниже мы предполагаем, что проблема относится к области полушария.

Текст задачи 10 звучит так: «Пример расчета корзины. Вам дается корзина с отверстием 4 1/2. Какова ее поверхность? Возьмите 1/9 из 9 (поскольку) корзина - это половина яйца. -shell. Вы получаете 1. Вычислите остаток, который равен 8. Вычислите 1/9 от 8. Вы получите 2/3 + 1/6 + 1/18. Найдите остаток от этой 8 после вычитания 2/3 + 1/6 + 1/18. Вы получите 7 + 1/9. Умножьте 7 + 1/9 на 4 + 1/2. Вы получите 32. Вот это его область. Вы нашли ее правильно ».^[1]^[5]

Решение сводится к вычислению площади как

{ displaystyle { text {Area}} = left ({ frac {2 times 8} {9}} right) ^ {2} times ({ text {Diameter}}) ^ {2} = { frac {256} {81}} ({ text {диаметр}}) ^ {2}}

Это значит, что писец Московского папируса использовал ${ displaystyle { frac {256} {81}} приблизительно 3,16049}$ к приблизительно π.

Задача 14: Объем усеченной пирамиды квадратной пирамиды

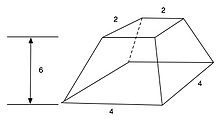
Четырнадцатая задача Московского математического журнала вычисляет объем усеченный.

Задача 14 утверждает, что пирамида была усечена таким образом, что верхняя область представляет собой квадрат длиной 2 единицы, нижняя часть - квадрат длиной 4 единицы и высотой 6 единиц, как показано. Объем составляет 56 кубических единиц, что правильно.^[1]

Текст этого примера звучит так: «Если вам скажут: усеченная пирамида из 6 для вертикальной высоты, 4 на основании и 2 на вершине: вы должны возвести 4 в квадрат; результат 16. Вы должны удвоить 4. ; результат 8. Вы должны возвести в квадрат эти 2, результат 4. Вам нужно сложить 16, 8 и 4. результат 28. Вы должны взять 1/3 из 6. Результат 2. Вы должны взять 28 дважды; результат 56. Видите, это 56. Вы найдете [это] правильным " ^[6]

Решение проблемы указывает на то, что египтяне знали правильную формулу для получения объем из усеченная пирамида:

{ displaystyle V = { frac {1} {3}} h (a ^ {2} + ab + b ^ {2})}

куда а и б - длина основания и верхней стороны усеченной пирамиды и час это высота. Исследователи предположили, как египтяне могли прийти к формуле для определения объема усеченный но вывод этой формулы не приводится в папирусе.^[7]

Резюме

Ричард Дж. Гиллингс кратко изложил содержание Папируса.^[8] Цифры с чертой обозначают единичная дробь имея этот номер как знаменатель, например ${ displaystyle { bar {4}} = { frac {1} {4}}}$ ; единичные дроби были обычным объектом изучения древнеегипетской математики.

Содержание Московского математического папируса^[а]
Нет.	Деталь.
1	Поврежденный и нечитаемый.
2	Поврежденный и нечитаемый.
3	Кедровая мачта. ${ displaystyle { bar {3}} ; { bar {5}}}$ из ${ displaystyle 30 = 16}$ . Неясно.
4	Площадь треугольника. ${ displaystyle { bar {2}}}$ из ${ Displaystyle 4 раз 10 = 20}$ .
5	Песус из буханок и хлеба. То же, что № 8.
6	Прямоугольник, площадь ${ displaystyle = 12, b = { bar {2}} ; { bar {4}} l}$ . Находить ${ displaystyle l}$ и ${ displaystyle b}$ .
7	Треугольник, площадь ${ displaystyle = 20, h = 2 ; { bar {2}} b}$ . Находить ${ displaystyle h}$ и ${ displaystyle b}$ .
8	Песус из буханок и хлеба.
9	Песус из буханок и хлеба.
10	Площадь криволинейной поверхности полусферы (или цилиндра).
11	Буханки и корзина. Неясно.
12	Песу из пива. Неясно.
13	Песус из хлебов и пива. То же, что № 9.
14	Объем усеченной пирамиды. ${ Displaystyle V = (ч / 3) (a ^ {2} + ab + b ^ {2})}$ .
15	Песу из пива.
16	Песу из пива. Аналогичен № 15.
17	Треугольник, площадь ${ displaystyle = 20, b = ({ bar {3}} ; { bar {15}}) h}$ . Находить ${ displaystyle h}$ и ${ displaystyle b}$ .
18	Мерная ткань в локтях и ладонях. Неясно.
19	Решите уравнение, ${ displaystyle 1 ; { bar {2}} x + 4 = 10}$ . Прозрачный.
20	Песу ${ displaystyle 1,000}$ буханки. Фракции Гора-Глаз.
21	Замешивание жертвенного хлеба.
22	Песус из хлебов и пива. Обмен.
23	Вычисление работы сапожника. Неясно. Пит говорит очень сложно.
24	Обмен хлебов и пива.
25	Решите уравнение, ${ displaystyle 2x + x = 9}$ . Элементарно и понятно.

Другие папирусы

Другие математические тексты из Древнего Египта включают:

Общие папирусы:

Таблицы 2 / n см .:

Таблица РМП 2 / н

Смотрите также

Список древнеегипетских папирусов

Примечания

^ Эта таблица является дословным воспроизведением Жиллингса, Математика во времена фараонов, стр. 246-247. Опускаются только ссылки на другие главы. Описание проблем 5, 8-9, 13, 15, 20-22 и 24 завершается «См. Главу 12». Для получения информации о проблемах Pesu описание проблемы 19 завершается словами «См. главу 14.» для получения информации о линейных и квадратных уравнениях, а также описания задач 10 и 14, завершенных «См. главу 18». для получения информации о площадях полуцилиндров или полусфер.