Седло обезьяны - Monkey saddle

Седло обезьяны

В математика, то седло обезьяны это поверхность определяется уравнением

${\displaystyle z=x^{3}-3xy^{2},\,}$

или в цилиндрические координаты

${\displaystyle z=\rho ^{3}\cos(3\varphi ).}$

Он принадлежит к классу седловые поверхности, и его название происходит от наблюдения, что седло для обезьяна потребуются два углубления для ног и одно для хвоста. Точка (0,0,0) на седле обезьяны соответствует вырожденная критическая точка функции z(Икс,у) в точке (0, 0). Седло обезьяны имеет изолированный пупочная точка с нуля Гауссова кривизна в начале координат, а во всех остальных точках кривизна строго отрицательна.

Можно связать прямоугольные и цилиндрические уравнения, используя сложные числа ${\displaystyle x+iy=re^{i\varphi }}$:

${\displaystyle z=x^{3}-3xy^{2}=\operatorname {Re} [(x+iy)^{3}]=\operatorname {Re} [r^{3}e^{3i\varphi }]=r^{3}\cos(3\varphi ).}$

Заменив 3 в цилиндрическом уравнении на любое целое число k ≥ 1, можно создать седло с k депрессии.^[1]

Другая ориентация седла обезьяны - это Расплавленный лепесток определяется ${\displaystyle x+y+z+xyz=0}$, таким образом z-Ось седла обезьяны соответствует направлению (1,1,1) в лепестке Корюшка.^[2][3]

Расплавленный лепесток: ${\displaystyle x+y+z+xyz=0}$

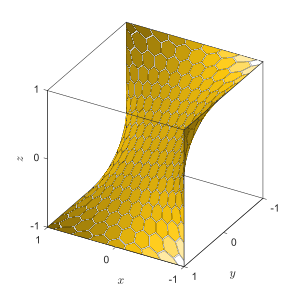
Седло для лошади

Период, термин седло лошади может использоваться в отличие от седла обезьяны, чтобы обозначить обычную поверхность седла, в которой z(Икс,у) имеет точка перевала, локальный минимум или максимум во всех направлениях ху-самолет. В отличие от седла обезьяны стационарное точка перегиба во всех направлениях.

Рекомендации

1. Пекхэм, С. (2011) Седло обезьяны, морской звезды и осьминога, Труды геоморфометрии 2011., Редлендс, Калифорния, стр. 31-34, http://geomorphometry.org/Peckham2011b.
2. Дж., Римротт, Ф. П. (1989). Вступительная динамика отношения. Нью-Йорк, штат Нью-Йорк: Springer New York. п. 26. ISBN  9781461235026. OCLC  852789976.
3. Chesser, H .; Римротт, Ф.П.Дж. (1985). Расмуссен, Х. (ред.). "Треугольник Магнуса и лепесток корюшки". CANCAM '85: Материалы десятого Канадского конгресса прикладной механики, 2-7 июня 1985 г., Университет Западного Онтарио, Лондон, Онтарио, Канада.

внешняя ссылка

• Вайсштейн, Эрик В. "Седло обезьяны". MathWorld.