Молекулярная вибрация - Molecular vibration

А молекулярная вибрация это периодическое движение из атомы из молекула относительно друг друга, так что центр масс молекулы остается неизменным. В типичный колебательные частоты, диапазон от менее 10¹³ Гц примерно до 10¹⁴ Гц, что соответствует волновые числа примерно от 300 до 3000 см⁻¹.

В общем случае нелинейная молекула с N атомов имеет 3N – 6 нормальные режимы вибрации, но линейный молекула имеет 3N - 5 мод, потому что вращение вокруг оси молекулы не наблюдается.^[1] А двухатомная молекула имеет один нормальный режим вибрации, так как он может только растягивать или сжимать одинарную связь. Колебания многоатомных молекул описываются в терминах нормальные режимы, которые не зависят друг от друга, но каждая нормальная мода включает одновременные колебания разных частей молекулы.

Колебание молекулы возбуждается, когда молекула поглощает энергию, ΔE, соответствующий частоте вибрации, ν, согласно соотношению ΔE = hν, куда час является Постоянная Планка. Фундаментальная вибрация возникает, когда один такой квант энергии поглощается молекулой в ее основное состояние. При поглощении нескольких квантов первый и, возможно, более высокий обертоны взволнованы.

В первом приближении движение при нормальной вибрации можно описать как своего рода простые гармонические колебания. В этом приближении энергия колебаний является квадратичной функцией (параболой) по отношению к атомным смещениям, и первый обертон имеет частоту в два раза выше основной. На самом деле вибрации ангармонический а частота первого обертона немного ниже, чем в два раза, чем у основного тона. Возбуждение высших обертонов вовлекает все меньше и меньше дополнительной энергии и в конечном итоге приводит к диссоциации молекулы, потому что потенциальная энергия молекулы больше похожа на Потенциал Морзе или, точнее, Морзе / дальний потенциал.

Колебательные состояния молекулы можно исследовать разными способами. Самый прямой путь - через ИК-спектроскопия, поскольку колебательные переходы обычно требуют количества энергии, которое соответствует инфракрасной области спектра. Рамановская спектроскопия, который обычно использует видимый свет, также может использоваться для непосредственного измерения частот вибрации. Эти два метода дополняют друг друга, и сравнение между ними может предоставить полезную структурную информацию, например, в случае правило взаимного исключения за центросимметричные молекулы.

Колебательное возбуждение может происходить вместе с электронным возбуждением в видимый в ультрафиолете область, край. Комбинированное возбуждение известно как вибронный переход, придавая вибрационную тонкую структуру электронные переходы, особенно для молекул в состояние газа.

Одновременное возбуждение вибрации и вращения вызывает вибрация-вращение спектры.

Количество вибрационных мод

Основная статья: Степени свободы (физика_и_химия)

Для молекулы с N атомов, позиции всех N ядра зависят в общей сложности от 3N координаты, так что в молекуле 3N степени свободы включая перевод, вращение и вибрация. Перевод соответствует перемещению центра масс, положение которого можно описать как 3 декартовы координаты.

Нелинейная молекула может вращаться вокруг любой из трех взаимно перпендикулярных осей и, следовательно, имеет 3 степени свободы вращения. Для линейной молекулы вращение вокруг оси молекулы не связано с движением какого-либо атомного ядра, поэтому есть только 2 степени свободы вращения, которые могут изменять координаты атомов.^[2][3]

Эквивалентным аргументом является то, что вращение линейной молекулы изменяет направление молекулярной оси в пространстве, что можно описать двумя координатами, соответствующими широте и долготе. Для нелинейной молекулы направление одной оси описывается этими двумя координатами, а ориентация молекулы вокруг этой оси обеспечивает третью координату вращения.^[4]

Таким образом, количество колебательных мод равно 3.N минус количество поступательных и вращательных степеней свободы, или 3N–5 для линейных и 3N–6 для нелинейных молекул.^[2][3][4]

Колебательные координаты

Координата нормальной вибрации представляет собой комбинацию изменения в положениях атомов в молекуле. При возбуждении вибрации координата изменяется синусоидально с частотой ν, частота вибрации.

Внутренние координаты

Внутренние координаты бывают следующих типов, проиллюстрированных на примере плоской молекулы этилен,

• Растяжение: изменение длины связи, например C – H или C – C.
• Изгиб: изменение угла между двумя связями, например, угла HCH в метиленовой группе.
• Раскачивание: изменение угла между группой атомов, такой как метиленовая группа, и остальной частью молекулы.
• Виляние: изменение угла между плоскостью группы атомов, такой как метиленовая группа, и плоскостью остальной части молекулы,
• Скручивание: изменение угла между плоскостями двух групп атомов, например изменение угла между двумя метиленовыми группами.
• Вне плоскости: изменение угла между любой из связей C – H и плоскостью, определяемой остальными атомами молекулы этилена. Другой пример - в BF₃ когда атом бора движется в плоскости трех атомов фтора и выходит из нее.

В координатах качания, виляния или скручивания длины связей внутри участвующих групп не меняются. Углы делают. Раскачивание отличается от покачивания тем, что атомы в группе остаются в одной плоскости.

В этене есть 12 внутренних координат: 4 C – H растяжения, 1 C – C растяжения, 2 H – C – H изгиба, 2 CH.₂ качалка, 2 CH₂ виляние, 1 скручивание. Обратите внимание, что углы H – C – C нельзя использовать в качестве внутренних координат, поскольку углы при каждом атоме углерода не могут увеличиваться одновременно.

Колебания метиленовой группы (–CH₂-) в молекуле для иллюстрации

Атомы в CH₂ группа, обычно встречающаяся в органические соединения, может вибрировать шестью разными способами: симметричное и асимметричное растяжение, стрижка, качание, виляние и скручивание как показано здесь:

Симметричный растяжение	Асимметричный растяжение	Ножницы (изгиб)
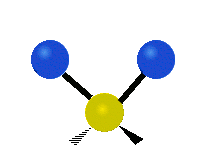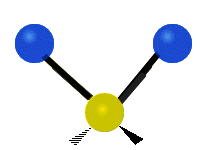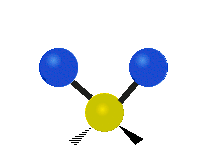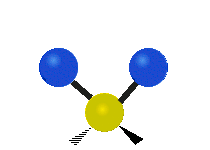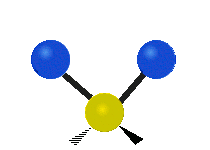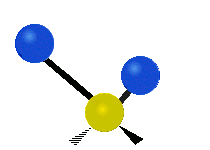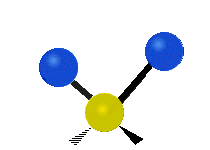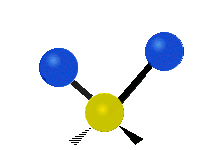Качалка	Виляние	Скручивание

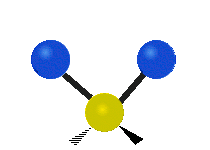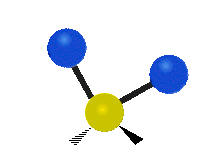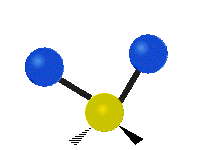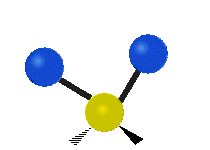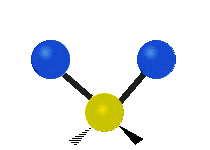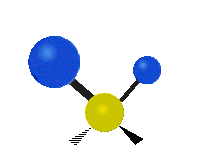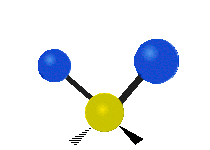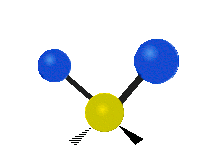(Эти цифры не отражают "отдача «атомов углерода, которые, хотя и обязательно присутствуют для уравновешивания общих движений молекулы, но намного меньше, чем движения более легких атомов H).

Координаты, адаптированные к симметрии

Смотрите также: Молекулярная симметрия

Координаты, адаптированные к симметрии, могут быть созданы путем применения оператор проекции к набору внутренних координат.^[5] Оператор проекции строится с помощью таблица символов молекулярного точечная группа. Например, четыре (ненормированные) координаты валентных колебаний C – H молекулы этена имеют вид

${displaystyle Q_{s1}=q_{1}+q_{2}+q_{3}+q_{4}!}$

${displaystyle Q_{s2}=q_{1}+q_{2}-q_{3}-q_{4}!}$

${displaystyle Q_{s3}=q_{1}-q_{2}+q_{3}-q_{4}!}$

${displaystyle Q_{s4}=q_{1}-q_{2}-q_{3}+q_{4}!}$

куда ${displaystyle q_{1}-q_{4}}$ - внутренние координаты растяжения каждой из четырех связей C – H.

Иллюстрации адаптированных к симметрии координат для большинства малых молекул можно найти в Накамото.^[6]

Нормальные координаты

Нормальные координаты, обозначенные как Q, относятся к положениям атомов вдали от их положений равновесия по отношению к нормальному режиму колебаний. Каждому нормальному режиму назначается одна нормальная координата, и поэтому нормальная координата относится к «продвижению» в этом нормальном режиме в любой момент времени. Формально нормальные режимы определяются путем решения векового определителя, а затем нормальные координаты (по нормальным режимам) могут быть выражены как суммирование по декартовым координатам (по позициям атомов). Нормальные моды диагонализируют матрицу, управляющую молекулярными колебаниями, так что каждая нормальная мода является независимой молекулярной вибрацией. Если молекула обладает симметрией, нормальные моды "преобразуются как" неприводимое представление под его точечная группа. Нормальные режимы определяются путем применения теории групп и проецирования неприводимого представления на декартовы координаты. Например, когда это лечение применяется к CO₂, обнаружено, что отрезки C = O не являются независимыми, а скорее существует симметричный участок O = C = O и асимметричный участок O = C = O:

• симметричное растяжение: сумма двух координат растяжения C – O; длины двух связей C – O изменяются на одинаковую величину, а атом углерода остается неподвижным. Q = q₁ + q₂
• асимметричное растяжение: разница двух координат растяжения C – O; длина одной связи C – O увеличивается, а другая - уменьшается. Q = q₁ - q₂

Когда две или более нормальные координаты принадлежат одному и тому же неприводимому представлению молекулярной точечной группы (в просторечии имеют одинаковую симметрию), происходит «смешивание», и коэффициенты комбинации не могут быть определены априори. Например, в линейной молекуле цианистый водород, HCN, Два валентных колебания

• в основном растяжение C – H с небольшим растяжением C – N; Q₁ = q₁ + а q₂ (а << 1)
• в основном растяжение C – N с небольшим растяжением C – H; Q₂ = b q₁ + q₂ (b << 1)

Коэффициенты a и b находятся путем выполнения полного нормального координатного анализа с помощью метода Вильсона. Метод GF.^[7]

Ньютоновская механика

В ЧАСCl молекула как ангармонический осциллятор, колеблющийся на уровне энергии E₃. D₀ является энергия диссоциации здесь, г₀ длина облигации, U потенциальная энергия. Энергия выражается в волновые числа. Молекула хлористого водорода присоединена к системе координат, чтобы показать изменения длины связи на кривой.

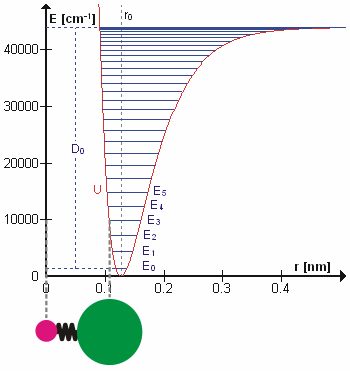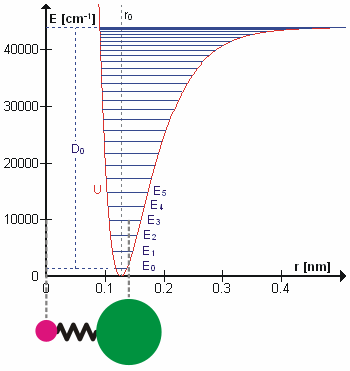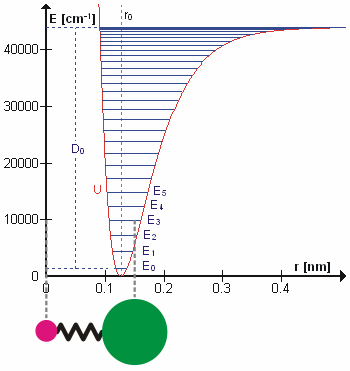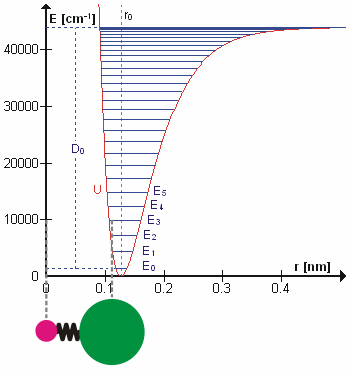
Возможно, что удивительно, но молекулярные колебания можно рассматривать с помощью механики Ньютона для расчета правильных частот колебаний. Основное предположение состоит в том, что каждую вибрацию можно рассматривать так, как если бы она соответствовала пружине. В гармоническом приближении пружина подчиняется Закон Гука: сила, необходимая для растяжения пружины, пропорциональна растяжению. Константа пропорциональности известна как силовая постоянная, k. Ангармонический осциллятор рассматривается в другом месте.^[8]

${displaystyle mathrm {Force} =-kQ!}$

К Второй закон движения Ньютона эта сила также равна уменьшенная масса, μ, раз ускорение.

${displaystyle mathrm {Force} =mu {frac {d^{2}Q}{dt^{2}}}}$

Поскольку это одна и та же сила, обыкновенное дифференциальное уравнение следует.

${displaystyle mu {frac {d^{2}Q}{dt^{2}}}+kQ=0}$

Решение этого уравнения простые гармонические колебания является

${displaystyle Q(t)=Acos(2pi u t); u ={1 over {2pi }}{sqrt {k over mu }}.!}$

А - максимальная амплитуда координаты колебания Q. Осталось определить приведенную массу, μ. В общем, приведенная масса двухатомной молекулы AB выражается через атомные массы: м_А и м_B, так как

${displaystyle {frac {1}{mu }}={frac {1}{m_{A}}}+{frac {1}{m_{B}}}.}$

Использование уменьшенной массы гарантирует, что вибрация не влияет на центр масс молекулы. В гармоническом приближении потенциальная энергия молекулы квадратично зависит от нормальной координаты. Отсюда следует, что силовая постоянная равна второй производной потенциальной энергии.

${displaystyle k={frac {partial ^{2}V}{partial Q^{2}}}}$

Когда два или более нормальных колебания имеют одинаковую симметрию, необходимо провести полный анализ нормальных координат (см. Метод GF ). Частоты колебаний,ν_я получены из собственные значения,λ_я, из матричный продукт GF. грамм представляет собой матрицу чисел, полученных из масс атомов и геометрии молекулы.^[7] F представляет собой матрицу, полученную из значений силовых постоянных. Подробности относительно определения собственных значений можно найти в.^[9]

Квантовая механика

В гармоническом приближении потенциальная энергия является квадратичной функцией нормальных координат. Решение Волновое уравнение Шредингера, энергетические состояния для каждой нормальной координаты имеют вид

${displaystyle E_{n}=hleft(n+{1 over 2}ight)u =hleft(n+{1 over 2}ight){1 over {2pi }}{sqrt {k over m}}!}$,

куда п - квантовое число, которое может принимать значения 0, 1, 2 ... В молекулярной спектроскопии, где изучаются несколько типов молекулярной энергии и используются несколько квантовых чисел, это колебательное квантовое число часто обозначается как v.^[10][11]

Разница в энергии при п (или же v) изменяется на 1, следовательно, равно ${displaystyle hu }$, продукт Постоянная Планка и частота вибрации, полученная с помощью классической механики. Для перехода с уровня п выровнять п + 1 из-за поглощения фотона частота фотона равна классической частоте колебаний ${displaystyle u }$ (в приближении гармонического осциллятора).

Видеть квантовый гармонический осциллятор для графиков первых 5 волновых функций, которые позволяют правила отбора будут сформулированы. Например, для гармонического осциллятора переходы разрешены только тогда, когда квантовое число п меняется на единицу,

${displaystyle Delta n=pm 1}$

но это не относится к ангармоническому осциллятору; наблюдение обертонов возможно только потому, что вибрации ангармоничны. Еще одно следствие ангармонизма - переходы между состояниями п= 2 и п= 1 имеют немного меньшую энергию, чем переходы между основным и первым возбужденным состояниями. Такой переход порождает горячая группа. Для описания колебательных уровней ангармонического осциллятора Расширение Данхэма используется.

Интенсивность

В инфракрасном спектре интенсивность полосы поглощения пропорциональна производной от молекулярный дипольный момент по нормальной координате.^[12] Точно так же интенсивность полос комбинационного рассеяния зависит от производной поляризуемость по нормальной координате. Также существует зависимость от четвертой степени длины волны используемого лазера.

Смотрите также

• Когерентная антистоксовая рамановская спектроскопия
• Условия Эккарта
• Ферми-резонанс
• Метод GF
• Инфракрасная спектроскопия карбонилов металлов
• Потенциал Леннарда – Джонса
• Спектроскопия в ближней инфракрасной области
• Ядерно-резонансная колебательная спектроскопия
• Резонансная рамановская спектроскопия
• Переходный дипольный момент

Рекомендации

1. Ландау, Л. Д .; Лифшиц, Э. М. (1976). Механика (3-е изд.). Pergamon Press. ISBN  0-08-021022-8.
2. Холлас, Дж. М. (1996). Современная спектроскопия (3-е изд.). Джон Вили. п. 77. ISBN  0471965227.
3. Banwell, Colin N .; Маккэш, Элейн М. (1994). Основы молекулярной спектроскопии (4-е изд.). Макгроу Хилл. п.71. ISBN  0-07-707976-0.
4. Аткинс, П. У .; Паула, Дж. Де (2006). Физическая химия (8-е изд.). Нью-Йорк: В. Х. Фриман. п.460. ISBN  0716787598.
5. Коттон, Ф. А. (1971). Химические приложения теории групп (2-е изд.). Нью-Йорк: Вили. ISBN  0471175706.
6. Накамото, К. (1997). Инфракрасные и рамановские спектры неорганических и координационных соединений, часть A (5-е изд.). Нью-Йорк: Вили. ISBN  0471163945.
7. Wilson, E.B .; Decius, J.C .; Кросс, П. С. (1995) [1955]. Молекулярные колебания. Нью-Йорк: Дувр. ISBN  048663941X.
8. Калифано, С. (1976). Колебательные состояния. Нью-Йорк: Вили. ISBN  0471129968.
9. Ганс, П. (1971). Вибрирующие молекулы. Нью-Йорк: Чепмен и Холл. ISBN  0412102900.
10. Холлас, Дж. М. (1996). Современная спектроскопия (3-е изд.). Джон Вили. п. 21. ISBN  0471965227.
11. Аткинс, П. У .; Паула, Дж. Де (2006). Физическая химия (8-е изд.). Нью-Йорк: У. Х. Фриман. стр.291 и 453. ISBN  0716787598.
12. Стил, Д. (1971). Теория колебательной спектроскопии. Филадельфия: В. Б. Сондерс. ISBN  0721685803.

дальнейшее чтение

• Шервуд П.М.А. (1972). Колебательная спектроскопия твердых тел. Издательство Кембриджского университета. ISBN  0521084822.

внешняя ссылка

• Код Free Molecular Vibration, разработанный Zs. Сабо и Р. Сципиони
• Молекулярная вибрация и поглощение
• небольшое объяснение колебательных спектров и таблица с силовыми константами.
• Таблицы символов для химически важных точечных групп