Минимаксная оценка - Minimax estimator

В статистических теория принятия решений, где перед нами стоит задача оценки детерминированного параметра (вектора) ${\displaystyle \theta \in \Theta }$ из наблюдений ${\displaystyle x\in {\mathcal {X}},}$ ан оценщик (правило оценки) ${\displaystyle \delta ^{M}\,\!}$ называется минимакс если его максимальный рисковать минимальна среди всех оценок ${\displaystyle \theta \,\!}$. В некотором смысле это означает, что ${\displaystyle \delta ^{M}\,\!}$ это оценщик, который работает лучше всего в наихудшем из возможных случаев, допускаемых в задаче.

Настройка проблемы

Рассмотрим задачу оценки детерминированного (не Байесовский ) параметр ${\displaystyle \theta \in \Theta }$ от зашумленных или поврежденных данных ${\displaystyle x\in {\mathcal {X}}}$ связанные через условное распределение вероятностей ${\displaystyle P(x\mid \theta )\,\!}$. Наша цель - найти "хороший" оценщик. ${\displaystyle \delta (x)\,\!}$ для оценки параметра ${\displaystyle \theta \,\!}$, что минимизирует некоторые заданные функция риска ${\displaystyle R(\theta ,\delta )\,\!}$. Здесь функция риска (технически Функциональный или Оператор поскольку ${\displaystyle R}$ функция функции, НЕ композиция функции) ожидание некоторых функция потерь ${\displaystyle L(\theta ,\delta )\,\!}$ относительно ${\displaystyle P(x\mid \theta )\,\!}$. Популярный пример функции потерь^[1] это квадрат ошибки потери ${\displaystyle L(\theta ,\delta )=\|\theta -\delta \|^{2}\,\!}$, а функцией риска для этой потери является среднеквадратичная ошибка (MSE).

К сожалению, в целом риск нельзя минимизировать, так как он зависит от неизвестного параметра. ${\displaystyle \theta \,\!}$ сам (если бы мы знали, какова реальная стоимость ${\displaystyle \theta \,\!}$, нам не нужно было бы его оценивать). Поэтому требуются дополнительные критерии для поиска оптимальной оценки в некотором смысле. Одним из таких критериев является минимаксный критерий.

Определение

Определение : Оценщик ${\displaystyle \delta ^{M}:{\mathcal {X}}\rightarrow \Theta \,\!}$ называется минимакс относительно функции риска ${\displaystyle R(\theta ,\delta )\,\!}$ если он достигает наименьшего максимального риска среди всех оценщиков, что означает, что он удовлетворяет

${\displaystyle \sup _{\theta \in \Theta }R(\theta ,\delta ^{M})=\inf _{\delta }\sup _{\theta \in \Theta }R(\theta ,\delta ).\,}$

Наименее благоприятное распределение

По логике, оценка является минимаксной, когда она является наилучшей в худшем случае. Продолжая эту логику, минимаксный оценщик должен быть Байесовская оценка относительно наименее благоприятного априорного распределения ${\displaystyle \theta \,\!}$. Чтобы продемонстрировать это понятие, обозначим средний риск байесовской оценки ${\displaystyle \delta _{\pi }\,\!}$ относительно предшествующего распределения ${\displaystyle \pi \,\!}$ так как

${\displaystyle r_{\pi }=\int R(\theta ,\delta _{\pi })\,d\pi (\theta )\,}$

Определение: Предварительное распространение ${\displaystyle \pi \,\!}$ называется наименее благоприятным, если для любого другого распределения ${\displaystyle \pi '\,\!}$ средний риск удовлетворяет ${\displaystyle r_{\pi }\geq r_{\pi '}\,}$.

Теорема 1: Если ${\displaystyle r_{\pi }=\sup _{\theta }R(\theta ,\delta _{\pi }),\,}$ тогда:

1. ${\displaystyle \delta _{\pi }\,\!}$ является минимаксным.
2. Если ${\displaystyle \delta _{\pi }\,\!}$ является уникальной байесовской оценкой, а также уникальной минимаксной оценкой.
3. ${\displaystyle \pi \,\!}$ наименее благоприятен.

Следствие: Если байесовский оценщик имеет постоянный риск, он минимальный. Учтите, что это необязательное условие.

Пример 1: недобросовестная монета^[2][3]: Рассмотрим задачу оценки «успешности» биномиальный Переменная, ${\displaystyle x\sim B(n,\theta )\,\!}$. Это можно рассматривать как оценку скорости, с которой несправедливая монета падает на «орла» или «решку». В этом случае байесовская оценка относительно Бета -распределенный приор, ${\displaystyle \theta \sim {\text{Beta}}({\sqrt {n}}/2,{\sqrt {n}}/2)\,}$ является

${\displaystyle \delta ^{M}={\frac {x+0.5{\sqrt {n}}}{n+{\sqrt {n}}}},\,}$

с постоянным байесовским риском

${\displaystyle r={\frac {1}{4(1+{\sqrt {n}})^{2}}}\,}$

и, согласно Следствию, является минимаксным.

Определение: Последовательность предшествующих распределений ${\displaystyle \pi _{n}\,\!}$ называется наименее благоприятным, если для любого другого распределения ${\displaystyle \pi '\,\!}$,

${\displaystyle \lim _{n\rightarrow \infty }r_{\pi _{n}}\geq r_{\pi '}.\,}$

Теорема 2: Если есть последовательность приоров ${\displaystyle \pi _{n}\,\!}$ и оценщик ${\displaystyle \delta \,\!}$ такой, что${\displaystyle \sup _{\theta }R(\theta ,\delta )=\lim _{n\rightarrow \infty }r_{\pi _{n}}\,\!}$, тогда :

1. ${\displaystyle \delta \,\!}$ является минимаксным.
2. Последовательность ${\displaystyle \pi _{n}\,\!}$ наименее благоприятен.

Обратите внимание, что здесь не гарантируется уникальность. Например, оценка ML из предыдущего примера может быть достигнута как предел байесовских оценок относительно униформа прежний, ${\displaystyle \pi _{n}\sim U[-n,n]\,\!}$ с увеличением поддержки, а также относительно нормального априорного значения с нулевым средним ${\displaystyle \pi _{n}\sim N(0,n\sigma ^{2})\,\!}$ с увеличением дисперсии. Таким образом, ни итоговая оценка ML не является уникальным минимаксом, ни наименее благоприятный априор не уникален.

Пример 2: Рассмотрим задачу оценки среднего значения ${\displaystyle p\,\!}$ размерный Гауссовский случайный вектор ${\displaystyle x\sim N(\theta ,I_{p}\sigma ^{2})\,\!}$. В максимальная вероятность (ML) оценка для ${\displaystyle \theta \,\!}$ в этом случае просто ${\displaystyle \delta _{\text{ML}}=x\,\!}$, и его риск

${\displaystyle R(\theta ,\delta _{\text{ML}})=E{\|\delta _{ML}-\theta \|^{2}}=\sum _{i=1}^{p}E(x_{i}-\theta _{i})^{2}=p\sigma ^{2}.\,}$

MSE оценки максимального правдоподобия в сравнении с оценкой Джеймса – Стейна

Риск постоянен, но оценка ML на самом деле не является байесовской, поэтому следствие теоремы 1 не применяется. Однако оценка ML является пределом байесовских оценок по отношению к предыдущей последовательности. ${\displaystyle \pi _{n}\sim N(0,n\sigma ^{2})\,\!}$, и, следовательно, действительно минимакс согласно теореме 2. Тем не менее из минимаксности не всегда следует допустимость. Фактически в этом примере известно, что оценка ML недопустима (не допустима) всякий раз, когда ${\displaystyle p>2\,\!}$. Известный Оценка Джеймса – Стейна доминирует над ML всякий раз, когда ${\displaystyle p>2\,\!}$. Хотя оба оценщика имеют одинаковый риск ${\displaystyle p\sigma ^{2}\,\!}$ когда ${\displaystyle \|\theta \|\rightarrow \infty \,\!}$, и оба они минимаксны, оценка Джеймса – Стейна имеет меньший риск для любых конечных ${\displaystyle \|\theta \|\,\!}$. Этот факт проиллюстрирован на следующем рисунке.

Несколько примеров

В общем, определить минимаксную оценку сложно, а зачастую и невозможно. Тем не менее, во многих случаях минимаксная оценка была определена.

Пример 3: ограниченное нормальное среднее: При оценке среднего значения вектора нормали ${\displaystyle x\sim N(\theta ,I_{n}\sigma ^{2})\,\!}$, где известно, что ${\displaystyle \|\theta \|^{2}\leq M\,\!}$. Байесовская оценка относительно априорной, которая равномерно распределена на краю ограничивающего сфера известен как минимаксный всякий раз, когда ${\displaystyle M\leq n\,\!}$. Аналитическое выражение для этой оценки:

${\displaystyle \delta ^{M}={\frac {nJ_{n+1}(n\|x\|)}{\|x\|J_{n}(n\|x\|)}},\,}$

где ${\displaystyle J_{n}(t)\,\!}$, это модифицированный Функция Бесселя первого вида заказап.

Асимптотическая минимаксная оценка

Сложность определения точной минимаксной оценки мотивировала изучение оценок асимптотического минимакса - оценки ${\displaystyle \delta '}$ называется ${\displaystyle c}$-асимптотический (или приближенный) минимакс, если

${\displaystyle \sup _{\theta \in \Theta }R(\theta ,\delta ')\leq c\inf _{\delta }\sup _{\theta \in \Theta }R(\theta ,\delta ).}$

Для многих задач оценивания, особенно в установках непараметрического оценивания, были установлены различные приближенные минимаксные оценки. Дизайн приближенной минимаксной оценки тесно связан с геометрией, такой как метрическое число энтропии, из ${\displaystyle \Theta }$.

Рандомизированная минимаксная оценка

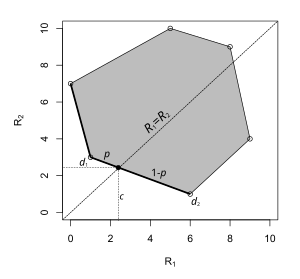
Иногда минимаксная оценка может принимать форму рандомизированное правило принятия решения. Пример показан слева. Пространство параметров состоит всего из двух элементов, и каждая точка на графике соответствует риску правила принятия решения: координата x - это риск, когда параметр ${\displaystyle \theta _{1}}$ а координата y - это риск, когда параметр равен ${\displaystyle \theta _{2}}$. В этой задаче принятия решения минимаксная оценка лежит на отрезке прямой, соединяющем две детерминированные оценки. Выбор ${\displaystyle \delta _{1}}$ с вероятностью ${\displaystyle 1-p}$ и ${\displaystyle \delta _{2}}$ с вероятностью ${\displaystyle p}$ сводит к минимуму риск супремума.

Связь с надежной оптимизацией

Надежная оптимизация представляет собой подход к решению задач оптимизации в условиях неопределенности в знании основных параметров.^[4][5] Например, Байесовская оценка MMSE параметра требует знания корреляционной функции параметра. Если знание этой корреляционной функции не полностью доступно, популярный подход минимаксной робастной оптимизации^[6] состоит в том, чтобы определить набор, характеризующий неопределенность в отношении корреляционной функции, а затем провести минимаксную оптимизацию по набору неопределенности и оценке соответственно. Аналогичные минимаксные оптимизации могут быть выполнены, чтобы сделать оценки устойчивыми к некоторым неточно известным параметрам. Например, недавнее исследование, посвященное таким методам в области обработки сигналов, можно найти в.^[7]

В R. Fandom Noubiap и W. Seidel (2001) был разработан алгоритм вычисления гамма-минимаксного решающего правила, когда гамма задается конечным числом обобщенных моментных условий. Такое решающее правило минимизирует максимум интегралов функции риска относительно всех распределений в гамме. Гамма-минимаксные решающие правила представляют интерес для исследований устойчивости в байесовской статистике.

использованная литература

• Э. Л. Леманн и Г. Каселла (1998), Теория точечного оценивания, 2-е изд. Нью-Йорк: Springer-Verlag.
• Ф. Перрон и Э. Маршанд (2002), "О минимаксной оценке ограниченного нормального среднего", Статистика и вероятностные письма 58: 327–333.
• Р. Фэндом Нубиап и У. Зайдель (2001), «Алгоритм для вычисления гамма-минимаксных правил принятия решений в условиях обобщенных моментов», Анналы статистики, Август 2001, т. 29, нет. 4. С. 1094–1116.
• Штейн, К. (1981). «Оценка среднего многомерного нормального распределения». Анналы статистики. 9 (6): 1135–1151. Дои:10.1214 / aos / 1176345632. Г-Н  0630098. Zbl  0476.62035.

1. Бергер, Дж. (1985). Статистическая теория принятия решений и байесовский анализ (2-е изд.). Нью-Йорк: Springer-Verlag. С. xv + 425. ISBN  0-387-96098-8. Г-Н  0580664.
2. Hodges, Jr., J.L .; Леманн, Э. (1950). «Некоторые проблемы при оценивании минимаксной точки». Анна. Математика. Статист. 21 (2): 182–197. Дои:10.1214 / aoms / 1177729838. JSTOR  2236900. Г-Н  0035949. Zbl  0038.09802.
3. Штейнхаус, Гюгон (1957). «Проблема оценки». Анна. Математика. Статист. 28 (3): 633–648. Дои:10.1214 / aoms / 1177706876. JSTOR  2237224. Г-Н  0092313. Zbl  0088.35503.
4. С. А. Кассам и Х. В. Бедный (1985), "Надежные методы обработки сигналов: обзор", Труды IEEE, т. 73, стр. 433–481, март 1985 г.
5. А. Бен-Тал, Л. Эль-Гауи и А. Немировски (2009), «Робастная оптимизация», Princeton University Press, 2009.
6. С. Верду и Х. В. Пур (1984), "О минимаксной робастности: общий подход и приложения", IEEE Transactions по теории информации, т. 30, стр. 328–340, март 1984 г.
7. М. Датский Нисар. Минимаксная надежность в обработке сигналов для связи, Шейкер Верлаг, ISBN  978-3-8440-0332-1, Август 2011 г.