Лю Хуэйс π алгоритм - Liu Huis π algorithm
| Часть серия статей на |
| математическая константа π |
|---|
| 3.1415926535897932384626433... |
| Использует |
| Характеристики |
| Ценить |
| Люди |
| История |
| В культуре |
| похожие темы |

Лю Хуэй π алгоритм был изобретен Лю Хуэй (эт. 3 век), математик Цао Вэй Королевство. До его времени отношение длины окружности к его диаметру в Китае экспериментально часто принималось равным трем, тогда как Чжан Хэн (78–139) представили его как 3,1724 (от отношения небесного круга к диаметру Земли, 92/29) или как . Лю Хуэй не удовлетворила эта ценность. Он прокомментировал, что он был слишком большим и превышал отметку. Другой математик Ван Фань (219–257) при условии π ≈ 142/45 ≈ 3,156.[1] Все эти эмпирические π значения были с точностью до двух цифр (т. е. до одного десятичного знака). Лю Хуэй был первым китайским математиком, предложившим строгий алгоритм вычисления π с любой точностью. Расчет Лю Хуэя с 96-угольник при условии точности до пяти цифр: π ≈ 3,1416.
Лю Хуэй отметил в своем комментарии к Девять глав математического искусства,[2] что отношение длины окружности вписанного шестиугольника к диаметру круга равно трем, следовательно, π должно быть больше трех. Далее он предоставил подробное пошаговое описание итеративного алгоритма вычисления π с любой необходимой точностью по делению многоугольников пополам; он рассчитал π между 3.141024 и 3.142708 с 96-угольником; он предположил, что 3.14 было достаточно хорошим приближением, и выразил π как 157/50; он признал, что это число немного мало. Позже он изобрел гениальный быстрый метод чтобы улучшить его, и получил π ≈ 3,1416 только с 96-угольником, с точностью, сопоставимой с точностью от 1536-го. Его наиболее важным вкладом в эту область была его простая итеративная π алгоритм.
Площадь круга

Лю Хуэй утверждал:
- "Умножьте одну сторону шестиугольника на радиус (его описанной окружности), затем умножьте это на три, чтобы получить площадь двенадцатиугольника; если мы разрежем шестиугольник на двенадцатиугольник, умножим его сторону на радиус, а затем снова умножим на шесть, мы получим площадь 24-угольника; чем мельче мы разрезаем, тем меньше потери по отношению к площади круга, таким образом, при дальнейшем разрезании за разрезом площадь полученного многоугольника совпадет и станет единым с кругом; не будет потерь".
По-видимому, Лю Хуэй уже освоил концепцию предела.[3]
Кроме того, Лю Хуэй доказал, что площадь круга равна половине его окружности, умноженной на радиус. Он сказал:
"Между многоугольником и кругом есть лишний радиус. Умножьте лишний радиус на сторону многоугольника. Полученная область выходит за границу круга".
На схеме d = лишний радиус. Умножение d с одной стороны приводит к продолговатому ABCD что выходит за границу круга. Если сторона многоугольника мала (т. Е. У многоугольника очень много сторон), то избыточный радиус будет небольшим, следовательно, лишняя площадь будет небольшой.
Как на схеме, когда N → ∞, d → 0, и ABCD → 0.
"Умножьте сторону многоугольника на его радиус, и площадь удвоится; следовательно, умножьте половину окружности на радиус, чтобы получить площадь круга".
Когда N → ∞, половина окружности N-угольник приближается к полукругу, таким образом, половина длины окружности, умноженная на ее радиус, равна площади круга. Лю Хуэй не стал подробно объяснять этот вывод. Однако это самоочевидно, если использовать «принцип взаимного дополнения» Лю Хуэя, который он предоставил в другом месте. Девять глав математического искусства: Разрезать геометрическую фигуру на части, переставить части, чтобы сформировать другую форму, площадь двух фигур будет одинаковой.
Таким образом, переставив шесть зеленых треугольников, три синих треугольника и три красных треугольника в прямоугольник с шириной = 3L, и высота р показывает, что площадь двенадцатиугольника = 3RL.
В общем, умножая половину окружности N-угольник по радиусу дает площадь 2N-гон. Лю Хуэй неоднократно использовал этот результат в своей π алгоритм.
Лю Хуэй π неравенство

Лю Хуэй доказал неравенство, включающее π рассматривая площадь вписанных многоугольников с N и 2N стороны.
На схеме желтая область представляет область N-угольник, обозначаемый , а желтая область плюс зеленая область представляет площадь 2N-угольник, обозначаемый . Таким образом, зеленая зона представляет собой разницу между областями двухN-угольник и N-угольник:
Красная область равна зеленой области, а также . Так
- Желтая область + зеленая область + красная область =
Позволять представляют площадь круга. потом
Если принять радиус круга равным 1, то получим Лю Хуэй π неравенство:
Итерационный алгоритм
Эта секция возможно содержит оригинальные исследования. (Март 2009 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
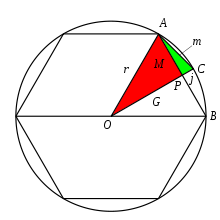
Лю Хуэй начал с вписанного шестиугольника. Позволять M быть длиной одной стороны AB шестиугольника, р это радиус круга.
Пополам AB с линией OPC, AC становится одной стороной двенадцатигранник (12-угольник), пусть его длина будет м. Пусть длина ПК быть j и длина OP быть грамм.
АОП, APC два прямоугольных треугольника. Лю Хуэй использовал Теорема Гоу Гу постоянно:
Отсюда теперь есть метод определения м из M, который дает длину стороны многоугольника с удвоенным числом ребер. Начиная с шестиугольник Лю Хуэй мог определить длину стороны двенадцатиугольника по этой формуле. Затем продолжайте снова и снова, чтобы определить длину стороны икоситетракон учитывая длину стороны двенадцатиугольника. Он мог делать это рекурсивно столько раз, сколько необходимо. Зная, как определить площадь этих многоугольников, Лю Хуэй мог приблизительно π.
С единиц, он получил
- зона 48-угольник
- площадь 96-угольника
- Разница 96-угольников и 48-угольников:
- из Лю Хуэй π неравенство:
- С р = 10,
- следовательно:
Он никогда не брал π как среднее значение от нижней границы 3,141024 и верхней границы 3,142704. Вместо этого он предположил, что 3.14 было достаточно хорошим приближением для π, и выразил его в виде дроби ; он указал, что это число немного меньше реального.
Лю Хуэй провел свои вычисления с стержневой камень, и выразил свои результаты с дробями. Однако итеративный характер Лю Хуэй π алгоритм довольно понятен:
в котором м - длина одной стороны многоугольника следующего порядка, деленная пополам от M. Один и тот же расчет выполняется многократно, каждый шаг требует только одного сложения и одного извлечения квадратного корня.
Быстрый метод
Вычисление квадратных корней из иррациональных чисел было непростой задачей в третьем веке, когдасчетные стержни. Лю Хуэй обнаружил сокращение, сравнивая разность площадей полигонов, и обнаружил, что доля разницы в площадях полигонов последовательного порядка составляет примерно 1/4.[4]
Позволять DN обозначают разницу в площадях N-угольник и (N/ 2) -угольник
Он нашел:
Следовательно:
Площадь круга единичного радиуса =
В котором
То есть все последующие лишние площади в сумме составляют одну треть от
- площадь единичного круга2
Лю Хуэй был вполне доволен этим результатом, потому что он получил тот же результат при вычислении 1536-угольника, получив площадь 3072-угольника. Это объясняет четыре вопроса:
- Почему он остановился на А192 в его презентации своего алгоритма. Потому что он открыл быстрый метод повышения точности π, достигая того же результата с 1536-угольником только с 96-угольником. В конце концов, вычисление квадратных корней было непростой задачей с стержневой камень. Используя быстрый метод, ему нужно было только выполнить еще одно вычитание, еще одно деление (на 3) и еще одно сложение вместо четырех дополнительных извлечений квадратного корня.
- Почему он предпочел вычислить π путем вычисления площадей вместо окружностей последовательных многоугольников, потому что быстрый метод требовал информации о разнице в области последовательных многоугольников.
- Кто был истинным автором параграфа, содержащего расчет
- Этот знаменитый абзац начинается со слов: «Бронзовый контейнер династии Хань на военном складе в Династия Цзинь.... ». Многие ученые, среди них Ёсио Миками и Джозеф Нидхэм, считал, что абзац «Бронзовый контейнер династии Хань» был работой Лю Хуэй, а не Цзу Чунчжи, как считали другие, из-за сильной корреляции этих двух методов через вычисление площади, и потому что не было ни одного слова, упоминающего 3,1415926 Зу π <3.1415927 результат, полученный через 12288-угольник.
Более поздние разработки
Лю Хуэй разработал надежный алгоритм для расчета π с любой точностью.
- Цзу Чунчжи был знаком с работами Лю Хуэя и получил большую точность, применив свой алгоритм к 12288-угольнику.
- Из формулы Лю Хуэя для 2N-угольник:
- Для 12288-угольника, вписанного в круг единичного радиуса:
- .
- Из Лю Хуэй π неравенство:
- В котором
- .
- Следовательно
Усечено до восьми значащих цифр:
- .
Это был знаменитый Цзу Чунчжи π неравенство.
Затем Цзу Чунчжи использовал формулу интерполяции Он Chengtian (何承天, 370-447) и получили приближенную дробь: .
Однако это π ценность исчезла в китайской истории на долгое время (например, математик династии Сун Цинь Цзюшао использовал π= и ), до того как Династия Юань математик Чжао Юцинь работал над вариацией Лю Хуэя π алгоритм, разделив пополам вписанный квадрат и снова получив [5]
Значение алгоритма Лю Хуэя
Лю Хуэй π алгоритм был одним из его самых важных вкладов в древнекитайскую математику. Он был основан на расчете N-угольная площадь, в отличие от алгоритма Архимеда, основанного на окружности многоугольника. С помощью этого метода Цзу Чунчжи получил восьмизначный результат: 3,1415926 < π <3,1415927, что является мировым рекордом по наиболее точному значению π в течение 1200 лет, даже к 1600 году в Европе, голландский математик Адриан Антонис и его сын получил π значение 3,1415929 с точностью до 7 цифр.[6]
Смотрите также
Примечания
Эта секция возможно содержит оригинальные исследования. (Март 2009 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
Быстрый метод Лю Хуэя потенциально мог дать почти такой же результат: 12288-угольник (3,141592516588) только с 96-угольником.
Рекомендации
- ^ Шеплер, Герман К. (1950), «Хронология числа Пи», Mathematics Magazine 23 (3): 165–170, ISSN 0025-570X.
- ^ Нидхэм, Том 3, 66.
- ^ Впервые заметил японский математик Ёсио Миками
- ^ Ёсио Миками: доктор философии. Диссертация 1932
- ^ Ёсио Миками сказал о работе Чжао Ю Синя: «Стороны и, следовательно, периметры этих многоугольников последовательно вычисляются таким образом, как это делал Лю Хуэй в былые времена», стр.136, Развитие математики в Китае и Японии
- ^ Роберт Темпл, Гений Китая, утонченное значение пи, стр. 144–145, ISBN 1-85375-292-4
дальнейшее чтение
- Нидхэм, Джозеф (1986). Наука и цивилизация в Китае: Том 3, Математика и науки о небе и Земле. Тайбэй: Caves Books, Ltd.
- Ву Вэньцзюнь ред, История китайской математики Том III (на китайском языке) ISBN 7-303-04557-0




















































