Гиперболическое движение (относительность) - Hyperbolic motion (relativity)

Гиперболическое движение движение объекта с постоянной правильное ускорение в специальная теория относительности. Это называется гиперболическим движением, потому что уравнение, описывающее путь объекта через пространство-время это гипербола, как это видно на графике на Диаграмма Минковского чьи координаты представляют собой подходящую инерциальную (неускоренную) систему отсчета. У этого движения есть несколько интересных особенностей, в том числе то, что его можно обогнать. фотон при наличии достаточной форы, как можно заключить из диаграммы.[1]
История
Герман Минковски (1908) показали связь между точкой на мировая линия и величина четырехскоростной и «гипербола кривизны» (Немецкий: Krümmungshyperbel).[2] В контексте Родилась жесткость, Макс Борн (1909) впоследствии ввел термин «гиперболическое движение» (Немецкий: Hyperbelbewegung) для случая постоянной величины четырехкратного ускорения, затем приводится подробное описание для заряжен частицы в гиперболическом движении, и ввел соответствующую «гиперболически ускоренную систему отсчета» (Немецкий: hyperbolisch beschleunigtes Bezugsystem).[3] Формулы Борна были упрощены и расширены Арнольд Зоммерфельд (1910).[4] Ранние отзывы можно найти в учебниках. Макс фон Лауэ (1911, 1921)[5] или же Вольфганг Паули (1921).[6] См. Также Galeriu (2015).[7] или Гургулхон (2013),[8] и Ускорение (специальная теория относительности) # История.
Мировая линия
Правильное ускорение частицы определяется как ускорение что частица "ощущает" ускорение от одного инерциальная система отсчета другому. Если собственное ускорение направлено параллельно линии движения, оно связано с обычным трёхускорение в специальной теории относительности к
куда - мгновенная скорость частицы, то Фактор Лоренца, это скорость света, и - координатное время. Решение для уравнение движения дает желаемые формулы, которые можно выразить через координатное время а также подходящее время . Для упрощения все начальные значения времени, местоположения и скорости могут быть установлены на 0, таким образом:[5][6][9][10][11]
(1)
Это дает , которая является гиперболой во времени T и переменной пространственного положения . В этом случае ускоряемый объект находится на вовремя . Если вместо этого есть начальные значения, отличные от нуля, формулы для гиперболического движения принимают вид:[12][13][14]
Быстрота
Мировую линию для гиперболического движения (которая с этого момента будет записываться как функция собственного времени) можно упростить несколькими способами. Например, выражение
может подвергнуться пространственному сдвигу суммы , таким образом
- ,[15]
при котором наблюдатель находится в позиции вовремя . Кроме того, установив и представляем быстрота ,[14] уравнения для гиперболического движения сводятся к[4][16]
(2)
с гиперболой .
Заряженные частицы в гиперболическом движении
Родился (1909 г.),[3] Зоммерфельд (1910),[4] фон Лауэ (1911),[5] Паули (1921)[6] также сформулировал уравнения для электромагнитное поле из заряженные частицы в гиперболическом движении.[7] Это было продлено Герман Бонди & Томас Голд (1955)[17] и Фултон и Рорлих (1960)[18][19]
Это связано с спорным[20][21] обсуждался вопрос, излучают ли заряды в вечном гиперболическом движении или нет, и согласуется ли это с принцип эквивалентности - даже если речь идет об идеальной ситуации, потому что вечное гиперболическое движение невозможно. В то время как ранние авторы, такие как Борн (1909) или Паули (1921), утверждали, что излучения не возникает, более поздние авторы, такие как Бонди и Голд[17] и Фултон и Рорлих[18][19] показал, что радиация действительно возникает.
Правильная система отсчета
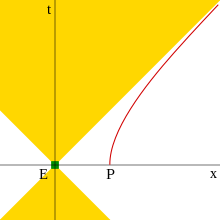
В уравнении (2) для гиперболического движения выражение была постоянной, тогда как скорость был переменным. Однако, как указывает Зоммерфельд,[16] можно определить как переменную, делая постоянный. Это означает, что уравнения становятся преобразованиями, указывающими на одновременную форму покоя ускоряемого тела с гиперболическими координатами глазами наблюдателя
Посредством этого преобразования собственное время становится временем гиперболически ускоренного кадра. Эти координаты, которые принято называть координатами Риндлера (аналогичные варианты называются Координаты Коттлера-Мёллера или координаты Ласса ), можно рассматривать как частный случай координат Ферми или Собственных координат и часто используются в связи с Эффект Унру. Используя эти координаты, оказывается, что наблюдатели в гиперболическом движении обладают очевидным горизонт событий, за пределами которого сигнал не может достичь их.
Специальное конформное преобразование
Менее известным методом определения системы отсчета при гиперболическом движении является использование специальное конформное преобразование, состоящий из инверсия, а перевод, и еще одна инверсия. Обычно это интерпретируется как калибровочное преобразование в пространстве Минковского, хотя некоторые авторы в качестве альтернативы используют его как преобразование ускорения (критический исторический обзор см. в Каструпе).[22] Он имеет вид
Использование только одного пространственного измерения , и дальнейшее упрощение, установив , и используя ускорение , следует[23]
с гиперболой . Получается, что при время становится единичным, к которому Фултон, Рорлих и Виттен[23] замечание, что нужно держаться подальше от этого лимита, а Каструп[22] (который очень критически относится к интерпретации ускорения) отмечает, что это один из странных результатов этой интерпретации.
Примечания
- ^ Миснер, Торн и Уиллер, 1973, Глава 6.
- ^ Минковский, Герман (1909). [Перевод Wikisource: Пространство и время ]. Jahresbericht der Deutschen Mathematiker-Vereinigung. Лейпциг.
- ^ а б Родился Макс (1909). "Теория звездных электронов в кинематике релятивистских принтов" [Перевод Wikisource: Теория жесткого электрона в кинематике принципа относительности ]. Annalen der Physik. 335 (11): 1–56. Bibcode:1909АнП ... 335 .... 1Б. Дои:10.1002 / andp.19093351102.
- ^ а б c Зоммерфельд, Арнольд (1910). "Zur Relativitätstheorie II: Vierdimensionale Vektoranalysis" [Перевод Wikisource: К теории относительности II: четырехмерный векторный анализ ]. Annalen der Physik. 338 (14): 649–689. Bibcode:1910АнП ... 338..649С. Дои:10.1002 / andp.19103381402.
- ^ а б c фон Лауэ, М. (1921). Die Relativitätstheorie, группа 1 (четвертое издание "Das Relativitätsprinzip" изд.). Vieweg. стр.89 –90, 155–166.; Первое издание 1911 г., второе расширенное издание 1913 г., третье расширенное издание 1919 г.
- ^ а б c Паули, Вольфганг (1921), "Die Relativitätstheorie", Encyclopädie der Mathematischen Wissenschaften, 5 (2): 539–776
По-английски: Паули, В. (1981) [1921]. Теория относительности. Фундаментальные теории физики. 165. Dover Publications. ISBN 0-486-64152-X. - ^ а б Галериу, К. (2017) [2015]. «Электрический заряд в гиперболическом движении: ранняя история». Архив истории точных наук. 71 (4): 1–16. arXiv:1509.02504. Дои:10.1007 / s00407-017-0191-x. S2CID 118510589.
- ^ Гургулхон, Э. (2013). Специальная теория относительности в общих рамках: от частиц до астрофизики. Springer. п. 396. ISBN 978-3642372766.
- ^ Мёллер, К. (1955). Теория относительности. Oxford Clarendon Press. стр.74 –75.
- ^ Риндлер, В. (1977). Основная теория относительности. Springer. стр.49 –50. ISBN 354007970X.
- ^ PhysicsFAQ (2016), «Релятивистская ракета», см. Внешние ссылки
- ^ Галлант, Дж. (2012). Заниматься физикой с помощью научной тетради: подход к решению проблем. Джон Вили и сыновья. С. 437–441. ISBN 978-0470665978.
- ^ Мюллер Т., Кинг А. и Адис Д. (2006). «Путешествие в конец вселенной и двойник» парадокс"". Американский журнал физики. 76 (4): 360–373. arXiv:физика / 0612126. Bibcode:2008AmJPh..76..360M. Дои:10.1119/1.2830528. S2CID 42983285.CS1 maint: несколько имен: список авторов (связь)
- ^ а б Фраундорф, П. (2012). «Введение в кинематику, ориентированное на путешественников»: IV – B. arXiv:1206.2877. Bibcode:2012arXiv1206.2877F. Цитировать журнал требует
| журнал =(помощь) - ^ Паули (1921), стр. 628, использовались обозначения куда
- ^ а б Зоммерфельд (1910), стр. 670-671 использовал форму и с мнимым углом и воображаемое время .
- ^ а б Бонди, Х., и Голд, Т. (1955). «Поле равномерно ускоренного заряда с особым упором на проблему ускорения свободного падения». Труды Лондонского королевского общества. 229 (1178): 416–424. Bibcode:1955RSPSA.229..416B. Дои:10.1098 / RSPA.1955.0098. S2CID 121563673.CS1 maint: несколько имен: список авторов (связь)
- ^ а б Фултон, Томас; Рорлих, Фриц (1960). «Классическое излучение равномерно ускоренного заряда». Анналы физики. 9 (4): 499–517. Bibcode:1960AnPhy ... 9..499F. Дои:10.1016/0003-4916(60)90105-6.
- ^ а б Рорлих, Фриц (1963). «Принцип эквивалентности». Анналы физики. 22 (2): 169–191. Bibcode:1963AnPhy..22..169R. Дои:10.1016/0003-4916(63)90051-4.
- ^ Стивен Лайл (2008). Равномерно ускоряющиеся заряженные частицы: угроза принципу эквивалентности. Springer. ISBN 978-3540684770.
- ^ Эйвинд Грён (2012). «Обзорная статья: Электродинамика излучающих зарядов». Успехи математической физики. 2012: 528631. Дои:10.1155/2012/528631.
- ^ а б Каструп, Х.А. (2008). «О достижениях конформных преобразований и связанных с ними симметрий в геометрии и теоретической физике». Annalen der Physik. 520 (9–10): 631–690. arXiv:0808.2730. Bibcode:2008AnP ... 520..631K. Дои:10.1002 / andp.200810324. S2CID 12020510.
- ^ а б Фултон Т., Рорлих Ф. и Виттен Л. (1962). «Физические последствия преобразования координат в равномерно ускоряющуюся систему отсчета». Il Nuovo Cimento. 26 (4): 652–671. Bibcode:1962NCim ... 26..652F. Дои:10.1007 / BF02781794. S2CID 121467786.CS1 maint: несколько имен: список авторов (связь)
Рекомендации
- Ли Пейдж (Февраль 1936 г.). "Новая теория относительности. Статья I. Фундаментальные принципы и преобразования между ускоренными системами". Физический обзор. 49 (3): 254–268. Bibcode:1936ПхРв ... 49..254П. Дои:10.1103 / PhysRev.49.254.
- Ли Пейдж и Норман И. Адамс (март 1936 г.). "Новая теория относительности. Статья II. Преобразование электромагнитного поля между ускоренными системами и уравнением силы". Физический обзор. 49 (6): 466–469. Bibcode:1936ПхРв ... 49..466П. Дои:10.1103 / PhysRev.49.466.
- Миснер, Чарльз В.; Торн, Кип. С.; Уилер, Джон А. (1973), Гравитация, В. Х. Фриман, Глава 6, ISBN 0-7167-0344-0
- Риндлер Вольфганг (1960). «Гиперболическое движение в искривленном пространстве-времени». Физический обзор. 119 (6): 2082–2089. Bibcode:1960ПхРв..119.2082Р. Дои:10.1103 / PhysRev.119.2082.
- Людвик Зильберштейн (1914): Теория относительности, стр.190.
- Набер, Грегори Л., Геометрия пространства-времени Минковского, Springer-Verlag, Нью-Йорк, 1992. ISBN 0-387-97848-8 (Твердая обложка), ISBN 0-486-43235-1 (Дуврское издание в мягкой обложке). С. 58–60.
внешняя ссылка
- FAQ по физике: Релятивистская ракета
- Математические страницы: Ускоренные путешествия, Излучает ли равномерно ускоряющийся заряд?

















![{ displaystyle { scriptstyle { begin {array} {c | c} { begin {align} u (T) & = { frac {u_ {0} gamma _ {0} + alpha T} { sqrt {1+ left ({ frac {u_ {0} gamma _ {0} + alpha T} {c}} right) ^ {2}}}} quad & = c tanh left { operatorname {arsinh} left ({ frac {u_ {0} gamma _ {0} + alpha T} {c}} right) right } X (T) & = X_ {0} + { frac {c ^ {2}} { alpha}} left ({ sqrt {1+ left ({ frac {u_ {0} gamma _ {0} + alpha T}) {c}} right) ^ {2}}} - gamma _ {0} right) & = X_ {0} + { frac {c ^ {2}} { alpha}} left { cosh left [ operatorname {arsinh} left ({ frac {u_ {0} gamma _ {0} + alpha T} {c}} right) right] - gamma _ {0} right } c tau (T) & = c tau _ {0} + { frac {c ^ {2}} { alpha}} ln left ({ frac {{ sqrt { c ^ {2} + left (u_ {0} gamma _ {0} + alpha T right) {} ^ {2}}} + u_ {0} gamma _ {0} + alpha T} { left (c + u_ {0} right) gamma _ {0}}} right) & = c tau _ {0} + { frac {c ^ {2}} { alpha} } left { operatorname {arsinh} left ({ frac {u_ {0} gamma _ {0} + alpha T} {c}} right) - operatorname {artanh} left ({ frac {u_ {0}} {c}} right) right } end {выравнивается}} & { begin {выравнивается} u ( tau) & = c tanh left { opera torname {artanh} left ({ frac {u_ {0}} {c}} right) + { frac { alpha tau} {c}} right } X ( tau) & = X_ {0} + { frac {c ^ {2}} { alpha}} left { cosh left [ operatorname {artanh} left ({ frac {u_ {0}} {c }} right) + { frac { alpha tau} {c}} right] - gamma _ {0} right } cT ( tau) & = cT_ {0} + { frac {c ^ {2}} { alpha}} left { sinh left [ operatorname {artanh} left ({ frac {u_ {0}} {c}} right) + { frac { alpha tau} {c}} right] - { frac {u_ {0} gamma _ {0}} {c}} right } end {align}} end {array}} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06b3bf81e2e1800bf5f97de52e2bc322b2f2ae18)

























