Расчет местоположения GNSS - GNSS positioning calculation
В глобальная навигационная спутниковая система (GNSS) определение местоположения приемника определяется с помощью шагов расчета или алгоритма, приведенных ниже. По сути, приемник GNSS измеряет время передачи сигналов GNSS, исходящих от четырех или более спутников GNSS (что дает псевдодиапазон ), и эти измерения используются для определения его положения (т. е. пространственные координаты ) и время приема.
Шаги расчета
- А глобальная навигационная спутниковая система (GNSS) приемник измеряет кажущееся время передачи,
 , или "фаза", сигналов GNSS, излучаемых четырьмя или более GNSS спутники (
, или "фаза", сигналов GNSS, излучаемых четырьмя или более GNSS спутники ( ), одновременно.[1]
), одновременно.[1] - Спутники GNSS передают сообщения спутников. эфемериды,
 , и собственное смещение часов (то есть опережение часов),
, и собственное смещение часов (то есть опережение часов),  [требуется разъяснение ] как функции (атомный ) стандартное время, например, GPST.[2]
[требуется разъяснение ] как функции (атомный ) стандартное время, например, GPST.[2] - Время передачи спутниковых сигналов GNSS,
 , таким образом, получается из не-закрытая форма уравнения
, таким образом, получается из не-закрытая форма уравнения  и
и  , куда
, куда  это релятивистский смещение часов, периодически повышающееся от спутника орбитальный эксцентриситет и Земли гравитационное поле.[2] Положение и скорость спутника определяются
это релятивистский смещение часов, периодически повышающееся от спутника орбитальный эксцентриситет и Земли гравитационное поле.[2] Положение и скорость спутника определяются  следующее:
следующее:  и
и  .
. - В области ГНСС "геометрический диапазон",
 , определяется как прямой или трехмерный расстояние,[3] из
, определяется как прямой или трехмерный расстояние,[3] из  к
к  в инерциальная система отсчета (например., С центром на Земле инерциальный (ECI) one), а не в вращающаяся рама.[2]
в инерциальная система отсчета (например., С центром на Земле инерциальный (ECI) one), а не в вращающаяся рама.[2] - Положение получателя,
 , и время приема,
, и время приема,  , удовлетворить световой конус уравнение
, удовлетворить световой конус уравнение  в инерциальная система отсчета, куда
в инерциальная система отсчета, куда  это скорость света. Время пролета сигнала от спутника до приемника составляет
это скорость света. Время пролета сигнала от спутника до приемника составляет  .
. - Вышесказанное распространяется на спутниковая навигация позиционирование уравнение,
 , куда
, куда  является атмосферная задержка (= ионосферная задержка + тропосферная задержка ) вдоль пути прохождения сигнала и
является атмосферная задержка (= ионосферная задержка + тропосферная задержка ) вдоль пути прохождения сигнала и  погрешность измерения.
погрешность измерения. - В Гаусс – Ньютон метод может быть использован для решения нелинейный проблема наименьших квадратов для решения:
 , куда
, куда  . Обратите внимание, что
. Обратите внимание, что  следует рассматривать как функцию
следует рассматривать как функцию  и
и  .
. - В апостериорное распределение из
 и
и  пропорционально
пропорционально  , чей Режим является
, чей Режим является  . Их вывод формализован как максимальная апостериорная оценка.
. Их вывод формализован как максимальная апостериорная оценка. - В апостериорное распределение из
 пропорционально
пропорционально  .
.
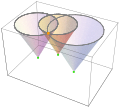
Проиллюстрированное решение
По сути, решение,  , является пересечением световые конусы.
, является пересечением световые конусы.
Корпус GPS

в котором  орбитальный эксцентрическая аномалия спутника
орбитальный эксцентрическая аномалия спутника  ,
,  это средняя аномалия,
это средняя аномалия,  это эксцентриситет, и
это эксцентриситет, и  .
.
- Вышеупомянутое можно решить, используя двумерный Ньютон – Рафсон метод на
 и
и  . В большинстве случаев потребуется и достаточно двух повторений. Его итеративное обновление будет описано с использованием приближенного обратный из Якобиан матрица следующим образом:
. В большинстве случаев потребуется и достаточно двух повторений. Его итеративное обновление будет описано с использованием приближенного обратный из Якобиан матрица следующим образом:

Дело ГЛОНАСС
- В ГЛОНАСС эфемериды не дают смещения часов
 , но
, но  .
.
Примечание
- В области GNSS,
 называется псевдодиапазон, куда
называется псевдодиапазон, куда  предварительное время приема получателя.
предварительное время приема получателя.  называется смещением часов приемника (т. е. опережением часов).[1]
называется смещением часов приемника (т. е. опережением часов).[1] - Выход стандартных GNSS-приемников
 и
и  за наблюдение эпоха.
за наблюдение эпоха. - Временное изменение смещения релятивистских часов спутника является линейным, если его орбита круговая (и, следовательно, его скорость одинакова в инерциальной системе отсчета).
- Время прохождения сигнала от спутника до приемника выражается как
 , чья правая сторона ошибка округления резистивный во время расчета.
, чья правая сторона ошибка округления резистивный во время расчета. - Геометрический диапазон рассчитывается как
 , где В центре Земли, фиксировано на Земле (ECEF) вращающаяся рама (например, WGS84 или же ITRF ) используется в правой части и
, где В центре Земли, фиксировано на Земле (ECEF) вращающаяся рама (например, WGS84 или же ITRF ) используется в правой части и  - вращающаяся матрица Земли с аргументом сигнала время пробега.[2] Матрицу можно факторизовать как
- вращающаяся матрица Земли с аргументом сигнала время пробега.[2] Матрицу можно факторизовать как  .
. - Единичный вектор прямой видимости спутника, наблюдаемого на
 описывается как:
описывается как:  .
. - В спутниковая навигация позиционирование уравнение может быть выражено с помощью переменные
 и
и  .
. - В нелинейность вертикальной зависимости тропосферная задержка ухудшает эффективность сходимости в Гаусс – Ньютон итераций на шаге 7.
- Приведенные выше обозначения отличаются от обозначений в статьях Википедии «Введение в расчет позиции» и «Расширенный расчет позиции» из спутниковая система навигации (GPS).
Смотрите также
Рекомендации
- ^ а б Мисра П. и Энге П., Глобальная система позиционирования: сигналы, измерения и производительность, 2-е, Ganga-Jamuna Press, 2006.
- ^ а б c d е ж Спецификация интерфейса NAVSTAR GLOBAL POSITIONING SYSTEM
- ^ 3-х мерный расстояние дан кем-то
 куда
куда  и
и  представлен в инерциальная система отсчета.
представлен в инерциальная система отсчета.
внешняя ссылка