Итерация с фиксированной точкой - Fixed-point iteration

Основная статья: Бесконечные композиции аналитических функций

В числовой анализ, итерация с фиксированной точкой это метод вычисления фиксированные точки функции.

Более конкретно, учитывая функцию ${\displaystyle f}$ определены на действительные числа с реальными ценностями и с учетом балла ${\displaystyle x_{0}}$ в домен из ${\displaystyle f}$, итерация с фиксированной точкой равна

${\displaystyle x_{n+1}=f(x_{n}),\,n=0,1,2,\dots }$

что порождает последовательность ${\displaystyle x_{0},x_{1},x_{2},\dots }$ который надеется сходиться в точку ${\displaystyle x}$. Если ${\displaystyle f}$ непрерывна, то можно доказать, что полученное ${\displaystyle x}$ неподвижная точка ${\displaystyle f}$, т.е.

${\displaystyle f(x)=x.\,}$

В более общем смысле функция ${\displaystyle f}$ можно определить на любом метрическое пространство со значениями в том же пространстве.

Примеры

• Первый простой и полезный пример - это Вавилонский метод для вычисления квадратный корень из а> 0, заключающийся в взятии ${\displaystyle f(x)={\frac {1}{2}}\left({\frac {a}{x}}+x\right)}$, т.е. среднее значение Икс и а / х, чтобы приблизиться к пределу ${\displaystyle x={\sqrt {a}}}$ (с любой начальной точки ${\displaystyle x_{0}\gg 0}$). Это частный случай Метод Ньютона цитируется ниже.

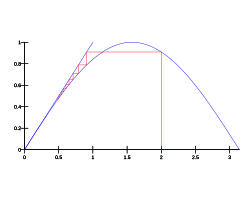
Итерация с фиксированной точкой Икс_п+1 = грех Икс_п с начальным значением Икс₀ = 2 сходится к 0. Этот пример не удовлетворяет предположениям Теорема Банаха о неподвижной точке и поэтому скорость его сходимости очень мала.

• Итерация с фиксированной точкой ${\displaystyle x_{n+1}=\cos x_{n}\,}$ сходится к единственной неподвижной точке функции ${\displaystyle f(x)=\cos x\,}$ для любой отправной точки ${\displaystyle x_{0}.}$ Этот пример действительно удовлетворяет предположениям Теорема Банаха о неподвижной точке. Следовательно, ошибка после n шагов удовлетворяет ${\displaystyle |x_{n}-x|\leq {q^{n} \over 1-q}|x_{1}-x_{0}|=Cq^{n}}$ (где мы можем взять ${\displaystyle q=0.85}$, если мы начнем с ${\displaystyle x_{0}=1}$.) Когда ошибка меньше кратной ${\displaystyle q^{n}}$ для некоторой постоянной q, мы говорим, что у нас есть линейная сходимость. Теорема Банаха о неподвижной точке позволяет получать итерации о неподвижной точке с линейной сходимостью.
• Итерация с фиксированной точкой ${\displaystyle x_{n+1}=2x_{n}\,}$ будет расходиться, если ${\displaystyle x_{0}=0}$. Мы говорим, что неподвижная точка ${\displaystyle f(x)=2x\,}$ отталкивает.
• Требование, чтобы ж непрерывно важно, как показывает следующий пример. Итерация

${\displaystyle x_{n+1}={\begin{cases}{\frac {x_{n}}{2}},&x_{n}\neq 0\\1,&x_{n}=0\end{cases}}}$

сходится к 0 для всех значений ${\displaystyle x_{0}}$.Однако 0 - это нет неподвижная точка функции

${\displaystyle f(x)={\begin{cases}{\frac {x}{2}},&x\neq 0\\1,&x=0\end{cases}}}$

поскольку эта функция нет непрерывно в ${\displaystyle x=0}$, и фактически не имеет неподвижных точек.

Приложения

• Метод Ньютона для нахождения корней заданной дифференцируемой функции ${\displaystyle f(x)}$ является

${\displaystyle x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}.}$

Если мы напишем ${\displaystyle g(x)=x-{\frac {f(x)}{f'(x)}}}$, мы можем переписать итерацию Ньютона как итерацию с фиксированной точкой

${\displaystyle x_{n+1}=g(x_{n})}$.

Если эта итерация сходится к фиксированной точке Икс из грамм, тогда

${\displaystyle x=g(x)=x-{\frac {f(x)}{f'(x)}}}$, так ${\displaystyle f(x)/f'(x)=0.}$

Обратное значение не равно нулю, поэтому ж(Икс) = 0: Икс это корень из ж. Согласно предположениям Теорема Банаха о неподвижной точке, итерация Ньютона, оформленная как метод фиксированной точки, демонстрирует линейная сходимость. Однако более подробный анализ показывает квадратичная сходимость, т.е.

${\displaystyle |x_{n}-x|<Cq^{2^{n}}}$, при определенных обстоятельствах.

• Метод Галлея похоже на Метод Ньютона но, когда он работает правильно, его ошибка ${\displaystyle |x_{n}-x|<Cq^{3^{n}}}$ (кубическая сходимость ). В общем, можно разработать методы, которые сходятся со скоростью ${\displaystyle Cq^{k^{n}}}$ для любого ${\displaystyle k\in \mathbb {N} }$. Как правило, чем выше k, чем он менее стабилен и тем более затратным в вычислительном отношении становится. По этим причинам методы более высокого порядка обычно не используются.
• Методы Рунге – Кутты и числовой обыкновенное дифференциальное уравнение решатели в целом можно рассматривать как итерации с фиксированной точкой. Действительно, основная идея при анализе А-стабильность решателей ODE следует начать с частного случая ${\displaystyle y'=ay}$, где a - это комплексное число, и чтобы проверить, сходится ли решатель ODE к фиксированной точке ${\displaystyle y=0}$ всякий раз, когда действительная часть отрицательна.^[а]
• В Теорема Пикара – Линделёфа, который показывает, что обыкновенные дифференциальные уравнения имеют решения, по сути является применением Теорема Банаха о неподвижной точке к специальной последовательности функций, которая образует итерацию с фиксированной точкой, строящую решение уравнения. Решение ОДУ таким образом называется Итерация Пикарда, Метод Пикарда, или Итерационный процесс Пикара.
• Возможность итераций в Excel может использоваться для поиска решений Уравнение Колбрука с точностью до 15 значащих цифр.^[1][2]

• Некоторые из схем «последовательного приближения», использованные в динамическое программирование решать Функциональное уравнение Беллмана основаны на итерациях с фиксированной точкой в ​​пространстве возвращаемой функции.^[3][4]

Схватки

Если функция ${\displaystyle f}$ определенная на реальной линии с реальными значениями Липшицева непрерывная с постоянной Липшица ${\displaystyle L<1}$, то эта функция имеет ровно одну фиксированную точку, и итерация с фиксированной точкой сходится к этой фиксированной точке для любого начального предположения ${\displaystyle x_{0}.}$ Эту теорему можно обобщить на любое полное метрическое пространство.

Доказательство этой теоремы:

С ${\displaystyle f}$ липшицево с константой Липшица ${\displaystyle L<1}$, то для последовательности ${\displaystyle \{x_{n},n=0,1,2,\ldots \}}$, у нас есть:

${\displaystyle {\begin{aligned}|x_{2}-x_{1}|=|f(x_{1})-f(x_{0})|&\leq L|x_{1}-x_{0}|,\\|x_{3}-x_{2}|=|f(x_{2})-f(x_{1})|&\leq L|x_{2}-x_{1}|,\\&\,\,\,\vdots \end{aligned}}}$

и

${\displaystyle |x_{n}-x_{n-1}|=|f(x_{n-1})-f(x_{n-2})|\leq L|x_{n-1}-x_{n-2}|.}$

Комбинирование приведенных выше неравенств дает:

${\displaystyle |x_{n}-x_{n-1}|\leq L^{n-1}|x_{1}-x_{0}|.}$

С ${\displaystyle L<1}$, ${\displaystyle L^{n-1}\rightarrow 0}$ в качестве ${\displaystyle n\rightarrow \infty .}$

Следовательно, мы можем показать ${\displaystyle \{x_{n}\}}$ это Последовательность Коши и, таким образом, он сходится к точке ${\displaystyle x^{*}}$.

Для итерации ${\displaystyle x_{n}=f(x_{n-1})}$, позволять ${\displaystyle n}$ уходят в бесконечность по обе стороны уравнения, получаем ${\displaystyle x^{*}=f(x^{*})}$. Это показывает, что ${\displaystyle x^{*}}$ фиксированная точка для ${\displaystyle f}$. Итак, мы доказали, что итерация в конечном итоге сходится к фиксированной точке.

Это свойство очень полезно, потому что не все итерации могут прийти к сходящейся фиксированной точке. При построении итерации с фиксированной точкой очень важно убедиться, что она сходится. Есть несколько теоремы о неподвижной точке чтобы гарантировать существование фиксированной точки, но поскольку итерационная функция является непрерывной, мы обычно можем использовать приведенную выше теорему, чтобы проверить, сходится ли итерация или нет. Доказательство обобщенной теоремы для полных метрических пространств аналогично.

Ускорение схождения

Скорость сходимости итерационной последовательности можно увеличить, используя ускорение схождения метод, такой как Дельта-квадрат процесс Эйткена. Применение метода Эйткена к итерации с фиксированной точкой известно как Метод Стеффенсена, и можно показать, что метод Стеффенсена дает скорость сходимости, по крайней мере, квадратичную.

Смотрите также

• Картирование сокращения
• Алгоритм поиска корней
• Теорема о неподвижной точке
• Комбинатор с фиксированной точкой
• Теорема Банаха о неподвижной точке
• Паутинный сюжет
• Цепь Маркова
• Бесконечные композиции аналитических функций
• Итерированная функция
• Сходимость и фиксированная точка

Рекомендации

1. Можно также считать определенные итерации A-стабильными, если итерации остаются ограниченными в течение длительного времени, что выходит за рамки данной статьи.

1. М. А. Кумар (2010), Решайте неявные уравнения (Коулбрук) на рабочем листе, Createspace, ISBN  1-4528-1619-0
2. Бркич, Деян (2017) Решение неявного уравнения Коулбрука для трения потока с использованием Excel, Электронные таблицы в образовании (eJSiE): Vol. 10: Вып. 2, статья 2. Доступно по адресу: https://sie.scholasticahq.com/article/4663-solution-of-the-implicit-colebrook-equation-for-flow-friction-using-excel
3. Беллман, Р. (1957). Динамическое программирование, Princeton University Press.
4. Снидович, М. (2010). Динамическое программирование: основы и принципы, Тейлор и Фрэнсис.

дальнейшее чтение

• Бэрден, Ричард Л .; Faires, Дж. Дуглас (1985). «Итерация с фиксированной точкой». Числовой анализ (Третье изд.). Издатели PWS. ISBN  0-87150-857-5.
• Хоффман, Джо Д.; Франкель, Стивен (2001). «Итерация с фиксированной точкой». Численные методы для инженеров и ученых (Второе изд.). Нью-Йорк: CRC Press. С. 141–145. ISBN  0-8247-0443-6.
• Джадд, Кеннет Л. (1998). «Итерация с фиксированной точкой». Численные методы в экономике. Кембридж: MIT Press. С. 165–167. ISBN  0-262-10071-1.

внешняя ссылка

• Алгоритмы с фиксированной точкой онлайн
• Онлайн-калькулятор итераций с фиксированной точкой (математический помощник в Интернете)