Фильтрация в контексте моделирование больших вихрей (LES) - математическая операция, предназначенная для удаления ряда мелких масштабов из решения в Уравнения Навье-Стокса. Поскольку основная трудность моделирования турбулентных потоков связана с широким диапазоном масштабов длины и времени, эта операция удешевляет моделирование турбулентных потоков за счет уменьшения диапазона масштабов, которые необходимо разрешить. LES-фильтр работает с низкими частотами, то есть он отфильтровывает шкалы, связанные с высокими частотами.
Гомогенные фильтры
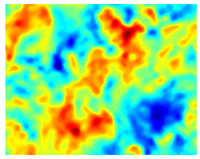
То же поле скорости DNS, отфильтрованное с использованием
коробчатый фильтр и
Δ = L/32
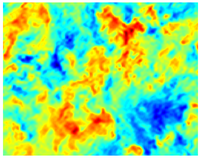
То же поле скорости DNS, отфильтрованное с использованием
коробчатый фильтр и
Δ = L/16Определение в физическом пространстве
Операция фильтрации нижних частот, используемая в LES, может применяться к пространственному и временному полю, например  . Операция фильтра LES может быть пространственной, временной или и тем, и другим. Отфильтрованное поле, обозначенное полосой, определяется как:[1][2]
. Операция фильтра LES может быть пространственной, временной или и тем, и другим. Отфильтрованное поле, обозначенное полосой, определяется как:[1][2]

куда  - ядро свертки, уникальное для используемого типа фильтра. Это можно записать как операцию свертки:
- ядро свертки, уникальное для используемого типа фильтра. Это можно записать как операцию свертки:

Ядро фильтра  использует длину отсечки и шкалы времени, обозначенные
использует длину отсечки и шкалы времени, обозначенные  и
и  соответственно. Чешуйки меньшего размера исключаются из
соответственно. Чешуйки меньшего размера исключаются из  Используя это определение, любое поле
Используя это определение, любое поле  может быть разделен на отфильтрованную и частично отфильтрованную (обозначенную штрихом) части, как
может быть разделен на отфильтрованную и частично отфильтрованную (обозначенную штрихом) части, как

Это также можно записать как операцию свертки,

Определение в спектральном пространстве
Операция фильтрации удаляет шкалы, связанные с высокими частотами, и, соответственно, операцию можно интерпретировать как Пространство Фурье. Для скалярного поля  в преобразование Фурье из
в преобразование Фурье из  является
является  функция
функция  пространственное волновое число, и
пространственное волновое число, и  временная частота.
временная частота.  можно отфильтровать по соответствующим преобразование Фурье ядра фильтра, обозначенного
можно отфильтровать по соответствующим преобразование Фурье ядра фильтра, обозначенного 

или же,

Ширина фильтра  имеет связанный волновой номер отсечки
имеет связанный волновой номер отсечки  и временная ширина фильтра
и временная ширина фильтра  также имеет связанную частоту среза
также имеет связанную частоту среза  Нефильтрованная часть
Нефильтрованная часть  является:
является:

Спектральная интерпретация операции фильтрации важна для операции фильтрации при моделировании больших вихрей, поскольку спектры турбулентных течений является центральным элементом подсеточных моделей LES, которые реконструируют эффект масштабов подфильтра (самые высокие частоты). Одна из задач подсеточного моделирования - эффективно имитировать каскад кинетической энергии от низких до высоких частот. Это делает спектральные свойства реализованного LES-фильтра очень важными для моделирования подсеток.
Свойства однородного фильтра
Однородные фильтры LES должны удовлетворять следующему набору свойств при применении к уравнениям Навье-Стокса.[1]
- 1. Сохранение констант
- Значение отфильтрованной константы должно быть равно константе,

- что означает,

- 2. Линейность

- 3. Коммутация с производными.

- Если ввести обозначения для коммутации операторов
![[f, g]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6d19d70e6a63d3650c33b1e58d1f69bbb956072) для двух произвольных операторов
для двух произвольных операторов  и
и  , куда
, куда
![[е, g] phi = f circ g ( phi) -g circ f ( phi) = f (g ( phi)) - g (f ( phi)),](https://wikimedia.org/api/rest_v1/media/math/render/svg/c16f02f51de3e6ea23348440769390f4ee0e1ea5)
- то это третье свойство можно выразить как
![left [G star, { frac { partial} { partial s}} right] = 0.](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ffc45070eaa4ca1d242e99c812ab5cb6d39c772)
Фильтры, удовлетворяющие этим свойствам, обычно не Операторы Рейнольдса, то есть сначала:

и во-вторых,

Неоднородные фильтры
Реализации операций фильтрации для всех потоков, кроме простейших, представляют собой операции неоднородной фильтрации. Это означает, что поток либо имеет непериодические границы, вызывающие проблемы с определенными типами фильтров, либо имеет непостоянную ширину фильтра.  , или оба. Это предотвращает коммутацию фильтра с производными, а операция коммутации приводит к нескольким дополнительным ошибочным членам:
, или оба. Это предотвращает коммутацию фильтра с производными, а операция коммутации приводит к нескольким дополнительным ошибочным членам:
![{ begin {array} {rcl} left [{ frac { partial} { partial { boldsymbol {x}}}}, G star right] phi & = & { frac { partial} { partial { boldsymbol {x}}}} left (G star phi right) -G star { frac { partial phi} { partial { boldsymbol {x}}}} & = & { frac { partial} { partial { boldsymbol {x}}}} int _ {{ Omega}} G ({ boldsymbol {x}} - { boldsymbol {r}}, Дельта ({ boldsymbol {x}}, t)) phi ({ boldsymbol {r}}, t) d { boldsymbol {r}} - G star { frac { partial phi} { partial { boldsymbol {x}}}} & = & left ({ frac { partial G} { partial Delta}} star phi right) { frac { partial Delta} { частичный x}} + int _ {{d Omega}} G (xr, Delta (x, t)) phi (r, t) { boldsymbol {n}} dS end {array}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e57745aa7084e0d0022df94ab931e87a98445e8)
куда  - вектор, нормальный к поверхности границы
- вектор, нормальный к поверхности границы  и
и  [1]
[1]
Оба члена появляются из-за неоднородностей. Первый связан с пространственным изменением размера фильтра.  а второй - из-за границы домена. Аналогично коммутация фильтра
а второй - из-за границы домена. Аналогично коммутация фильтра  с временной производной приводит к ошибке, возникающей из-за временного изменения размера фильтра,
с временной производной приводит к ошибке, возникающей из-за временного изменения размера фильтра,
![left [{ frac { partial} { partial t}}, G star right] = left ({ frac { partial G} { partial Delta}} star phi right) { frac { partial Delta} { partial t}}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/924c69bb805ddb80ca5ad23979fb9d5c77c964ac)
Было предложено несколько операций фильтрации, которые устраняют или минимизируют эти ошибки.[нужна цитата ]
Классические фильтры моделирования больших вихрей
![[значок]](//upload.wikimedia.org/wikipedia/commons/thumb/1/1c/Wiki_letter_w_cropped.svg/20px-Wiki_letter_w_cropped.svg.png) | Эта секция нуждается в расширении с: Правильное выравнивание участков. Вы можете помочь добавляя к этому. (Январь 2020) |
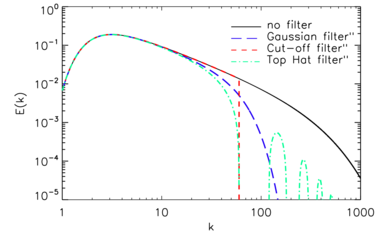
Турбулентный энергетический спектр и эффект от операций фильтрации
[3]Для пространственной фильтрации при моделировании больших вихрей обычно используются три фильтра. Определение  и
и  дается обсуждение важных свойств.[2]
дается обсуждение важных свойств.[2]
Коробчатый фильтр
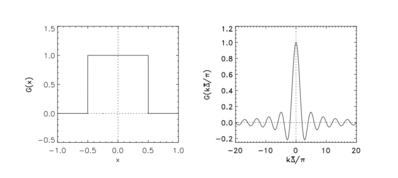
Коробчатый фильтр в физическом и спектральном пространстве
Ядро фильтра в физическом пространстве определяется следующим образом:

Ядро фильтра в спектральном пространстве определяется выражением:


Гауссов фильтр в физическом и спектральном пространстве
Гауссов фильтр
Ядро фильтра в физическом пространстве определяется следующим образом:

Ядро фильтра в спектральном пространстве определяется выражением:

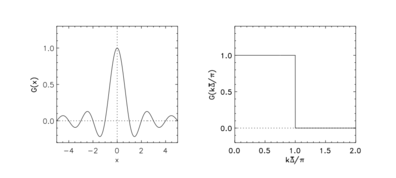
Четкий спектральный фильтр в физическом и спектральном пространстве
Четкий спектральный фильтр
Ядро фильтра в физическом пространстве определяется следующим образом:

Ядро фильтра в спектральном пространстве определяется выражением:

Смотрите также
Рекомендации

































![[f, g]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6d19d70e6a63d3650c33b1e58d1f69bbb956072)


![[е, g] phi = f circ g ( phi) -g circ f ( phi) = f (g ( phi)) - g (f ( phi)),](https://wikimedia.org/api/rest_v1/media/math/render/svg/c16f02f51de3e6ea23348440769390f4ee0e1ea5)
![left [G star, { frac { partial} { partial s}} right] = 0.](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ffc45070eaa4ca1d242e99c812ab5cb6d39c772)


![{ begin {array} {rcl} left [{ frac { partial} { partial { boldsymbol {x}}}}, G star right] phi & = & { frac { partial} { partial { boldsymbol {x}}}} left (G star phi right) -G star { frac { partial phi} { partial { boldsymbol {x}}}} & = & { frac { partial} { partial { boldsymbol {x}}}} int _ {{ Omega}} G ({ boldsymbol {x}} - { boldsymbol {r}}, Дельта ({ boldsymbol {x}}, t)) phi ({ boldsymbol {r}}, t) d { boldsymbol {r}} - G star { frac { partial phi} { partial { boldsymbol {x}}}} & = & left ({ frac { partial G} { partial Delta}} star phi right) { frac { partial Delta} { частичный x}} + int _ {{d Omega}} G (xr, Delta (x, t)) phi (r, t) { boldsymbol {n}} dS end {array}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e57745aa7084e0d0022df94ab931e87a98445e8)




![left [{ frac { partial} { partial t}}, G star right] = left ({ frac { partial G} { partial Delta}} star phi right) { frac { partial Delta} { partial t}}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/924c69bb805ddb80ca5ad23979fb9d5c77c964ac)







