Экзистенциальный граф - Existential graph
Эта статья может быть расширен текстом, переведенным с соответствующая статья на немецком. (Май 2017 г.) Щелкните [показать] для получения важных инструкций по переводу.
|
| Чарльз Сандерс Пирс |
|---|
| Общий |
| Философский |
| Биографический |
Сокращения B: x: Брент, Джозеф (1998), Чарльз Сандерс Пирс: Жизнь, 2-е издание, стр. X[1] CDPT: Commens Словарь терминов Пирса |
An экзистенциальный граф это тип схематический или визуальное обозначение логических выражений, предложенное Чарльз Сандерс Пирс, кто писал на графическая логика еще в 1882 г.,[2] и продолжал развивать метод до своей смерти в 1914 году.
Графики
Пирс предложил три системы экзистенциальных графов:
- альфа, изоморфный к сентенциальная логика и двухэлементная булева алгебра;
- бета, изоморфный логика первого порядка с тождеством, с закрытыми формулами;
- гамма, (почти) изоморфна нормальная модальная логика.
Альфа гнездится в бета и гамма. Бета не гнездится в гамма, квантифицированная модальная логика является более общей, чем предложенная Пирсом.
Альфа
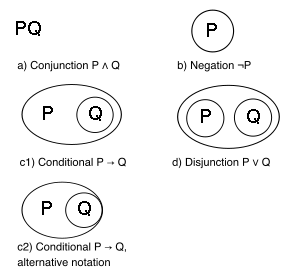
В синтаксис является:
- Пустая страница;
- Отдельные буквы или фразы, написанные в любом месте страницы;
- Любой граф можно заключить в простая замкнутая кривая называется резать или же сен. Отрезок может быть пустым. Вырезы могут встраиваться и сцепляться по желанию, но никогда не должны пересекаться.
Любая правильно построенная часть графа - это подграф.
В семантика находятся:
- Пустая страница обозначает Правда;
- Буквы, фразы, подграфы и целые графики могут быть Истинный или же Ложь;
- Заключить подграф вырезом эквивалентно логическому отрицание или логическое дополнение. Следовательно, пустой разрез означает Ложь;
- Все подграфы в данном разрезе неявно соединенный.
Следовательно альфа Графы - это минималистское обозначение сентенциальная логика, основанный на выразительной адекватности И и Нет. В альфа графики представляют собой радикальное упрощение двухэлементная булева алгебра и функторы истины.
В глубина объекта - это количество разрезов, которые его окружают.
Правила вывода:
- Вставка - любой подграф может быть вставлен в глубину с нечетным номером.
- Стирание - любой подграф с четной глубиной может быть удален.
Правила эквивалентности:
- Двойной разрез - пара разрезов, между которыми ничего нет, может быть проведена вокруг любого подграфа. Таким же образом можно стереть два вложенных разреза, между которыми ничего нет. Это правило эквивалентно булевой инволюции.
- Итерация / деитерация - чтобы понять это правило, лучше всего рассматривать график как древовидная структура имея узлы и предки. Любой подграф п в узле п может быть скопирован в любой узел в зависимости от п. Аналогично, любой подграф п в узле п могут быть удалены, если существует копия п в каком-то узле предка п (т.е. некоторый узел, на котором п зависит от). Для эквивалентного правила в алгебраическом контексте см. C2 в Законы формы.
Доказательство манипулирует графом серией шагов, каждый шаг оправдывается одним из приведенных выше правил. Если график можно поэтапно сократить до пустой страницы или пустого фрагмента, это то, что теперь называется тавтология (или его дополнение). Графики, которые нельзя упростить за определенную точку, являются аналогами удовлетворительный формулы из логика первого порядка.
Бета
Пирс отметил предикаты использование интуитивно понятных английских фраз; стандартные обозначения современной логики, заглавные латинские буквы, также могут быть использованы. Точка свидетельствует о существовании какого-либо человека в область дискурса. Несколько экземпляров одного и того же объекта связаны линией, называемой «линией идентичности». Нет буквального переменные или же кванторы в смысле логика первого порядка. Строку идентичности, соединяющую два или более предикатов, можно рассматривать как утверждение, что предикаты имеют общую переменную. Наличие линий идентичности требует изменения альфа правила эквивалентности.
Бета-графики можно рассматривать как систему, в которой все формулы следует рассматривать как замкнутые, потому что все переменные неявно количественно определены. Если «самая мелкая» часть строки идентичности имеет четную (нечетную) глубину, связанная переменная неявно экзистенциально (повсеместно ) количественно.
Земан (1964) первым заметил, что бета графики изоморфный к логика первого порядка с равенство (также см. Zeman 1967). Однако вторичная литература, особенно Робертс (1973) и Шин (2002), не согласны с тем, как это так. В трудах Пирса этот вопрос не рассматривается, потому что логика первого порядка была впервые четко сформулирована лишь через несколько лет после его смерти, в первом издании книги 1928 года. Дэвид Гильберт и Вильгельм Аккерманн с Принципы математической логики.
Гамма
Добавьте к синтаксису альфа второй вид простая замкнутая кривая, написанные пунктирной, а не сплошной линией. Пирс предложил правила для этого второго стиля огранки, который можно прочитать как примитивный унарный оператор из модальная логика.
Земан (1964) был первым, кто заметил, что прямые поправки гамма правила графа дают хорошо известные модальные логики S4 и S5. Следовательно гамма графики можно рассматривать как своеобразную форму нормальная модальная логика. Эта находка Земана осталась незамеченной по сей день, но, тем не менее, включена здесь как достопримечательность.
Роль Пирса
Экзистенциальные графы - любопытное детище Пирс то логик / математик с Пирсом, основателем основного направления семиотика. Графическая логика Пирса - лишь одно из его многочисленных достижений в области логики и математики. В серии статей, начинающейся в 1867 г. и завершающейся его классической статьей 1885 г. Американский журнал математики, Пирс разработал большую часть двухэлементная булева алгебра, пропозициональное исчисление, количественная оценка и исчисление предикатов, и некоторые элементарные теория множеств. Теоретики моделей считают Пирса первым в своем роде. Он также расширил алгебра отношений. Он остановился металогика (который ускользнул даже Principia Mathematica ).
Но развитие Пирса семиотический теория привела его к сомнению в ценности логики, сформулированной с использованием обычных линейных обозначений, и к предпочтению, чтобы логика и математика записывались в двух (или даже трех) измерениях. Его работа вышла за рамки Диаграммы Эйлера и Venn 1880 год пересмотр из них. Frege 1879 год Begriffsschrift также использовались двумерные обозначения логики, но очень отличающиеся от обозначений Пирса.
Первая опубликованная статья Пирса по графической логике (перепечатанная в томе 3 его Сборник статей) предложил систему, двойственную (по сути) альфа экзистенциальные графы, называемые увлекательные графики. Он очень скоро отказался от этого формализма в пользу экзистенциальных графов. В 1911 г. Виктория, леди Уэлби показал Экзистенциальные графы К. К. Огден кто чувствовал, что их можно с пользой объединить с мыслями Уэлби в «менее заумной форме».[3] В остальном они не привлекали к себе особого внимания в течение его жизни и неизменно очернялись или игнорировались после его смерти, пока не получил докторскую степень. диссертации Робертса (1964) и Земана (1964).
Смотрите также
Рекомендации
- ^ Брент, Джозеф (1998), Чарльз Сандерс Пирс: Жизнь, 2-е издание, Блумингтон и Индианаполис: Издательство Индианского университета (страница каталога ); также NetLibrary.
- ^ Пирс, К.С., «[О стыках и переломах в логике]» (название редакции MS 427 (новая система нумерации), осень – зима 1882 г.) и «Письмо Пирса к О.Х. Митчеллу» (L 294, 21 декабря 1882 г.) ), Произведения Чарльза С. Пирса, v. 4, "Junctures" на стр. 391–393 (Google предварительный просмотр ) и письмо на стр. 394–399 (Google предварительный просмотр ). Видеть Сова, Джон Ф. (1997), "Соответствие логической структуры лингвистической структуре", Исследования логики Чарльза Сандерса Пирса, Натан Хаузер, Дон Д. Робертс и Джеймс Ван Эвра, редакторы, Блумингтон и Индианополис: Indiana University Press, стр. 418–444, см. 420, 425, 426, 428.
- ^ Петрилли, Сьюзен (2017). Виктория Уэлби и наука о знаках: сигнифика, семиотика, философия языка. Рутледж. ISBN 978-1-351-29598-7.
дальнейшее чтение
Первичная литература
- 1931–1935 & 1958. Собрание статей Чарльза Сандерса Пирса. Том 4, Книга II: «Графики существования», состоит из параграфов 347–584. Обсуждение также начинается в пункте 617.
- Пункты 347–349 (II.1.1. «Логическая диаграмма») - определение Пирса «Логическая диаграмма (или график)» в Болдуин с Словарь философии и психологии (1902), т. 2, с. 28. Классика по истории психологии Eprint.
- Пункты 350–371 (II.1.2. «Диаграмм Эйлера») - из «Графиков» (рукопись 479) c. 1903 г.
- Пункты 372–584 Eprint.
- Параграфы 372–393 (II.2. «Символическая логика») - часть Пирса «Символической логики» Болдуина. Словарь философии и психологии (1902) т. 2, стр. 645 –650, начало (в верхней части второго столбца) со слов «Если определена символическая логика ...». Параграф 393 (DPP2 Болдуина, стр. 650) принадлежит Пирсу и Кристин Лэдд-Франклин ("C.S.P., C.L.F.").
- Параграфы 394–417 (II.3. «Экзистенциальные графы») - из брошюры Пирса Программа по некоторым темам логики, стр. 15–23, Альфред Мадж и сын, Бостон (1903 г.).
- Пункты 418–509 (II.4. «О графах существования, диаграммах Эйлера и логической алгебре») - из «Логических трактатов, № 2» (рукопись 492), c. 1903 г.
- Пункты 510–529 (II.5. «Гамма-часть экзистенциальных графов») - из «Лекций Лоуэлла 1903 года», лекция IV (рукопись 467).
- Параграфы 530–572 (II.6.) - «Пролегомены к извинению за прагматизм» (1906), Монист, т. XVI, п. 4. С. 492. -546. Исправления (1907 г.) в Монист т. XVII, п. 160.
- Параграфы 573–584 (II.7. «Улучшение гамма-графиков») - из «Для Национальной академии наук, апрельское собрание 1906 года в Вашингтоне» (рукопись 490).
- Параграфы 617–623 (по крайней мере) (в Книге III, гл. 2, §2, параграфы 594–642) - из «Некоторые удивительные лабиринты: первое объяснение любопытства», Монист, т. XVIII, 1908 г., п. 3. С. 416. -464, см. Начало п. 440.
- 1992. "Лекция третья: Логика родственников", Рассуждение и логика вещей С. 146–164. Кетнер, Кеннет Лейн (редактирование и введение) и Хилари Патнэм (комментарий). Издательство Гарвардского университета. Лекции Пирса в 1898 году в Кембридже, Массачусетс.
- 1977, 2001. Семиотика и значения: Переписка между К.С. Пирсом и Виктория Леди Велби. Хардвик, С.С., изд. Лаббок, Техас: Издательство Техасского Технического Университета. 2-е издание 2001 г.
- Транскрипция MS 514 Пирса (1909), под редакцией с комментариями Джон Сова.
В настоящее время хронологическое критическое издание произведений Пирса, Сочинения, распространяется только на 1892 год. Большая часть работ Пирса по логические графики состоит из рукописей, написанных после этой даты и до сих пор не опубликованных. Следовательно, наше понимание графической логики Пирса, вероятно, изменится по мере появления оставшихся 23 томов хронологического издания.
Вторичная литература
- Хаммер, Эрик М. (1998), "Семантика экзистенциальных графов", Журнал философской логики 27: 489–503.
- Кетнер, Кеннет Лейн
- (1981), "Лучший пример семиоза и его использование в обучении семиотике", Американский журнал семиотики v. I, n. 1–2, с. 47–83. Статья представляет собой введение в экзистенциальные графы.
- (1990), Элементы логики: введение в экзистенциальные графы Пирса, Texas Tech University Press, Лаббок, Техас, 99 страниц, в спиральном переплете.
- Кейруш, Жоао и Стьернфельт, Фредерик
- (2011), «Диаграмматические рассуждения и логическое представление Пирсана», Семиотика т. 186 (1/4). (Специальный выпуск о схематической логике Пирса.) [1]
- Робертс, Дон Д.
- (1964), «Экзистенциальные графы и естественная дедукция» в Мур, Э. К., и Робин, Р. С., ред., Исследования по философии К. С. Пирса, 2-я серия. Амхерст Массачусетс: Массачусетский университет Press. Первая публикация, показывающая сочувствие и понимание графической логики Пирса.
- (1973). Экзистенциальные графы К.С. Пирса. Джон Бенджаминс. Результат его диссертации 1963 года.
- Шин, Сон-Джу (2002), Культовая логика графов Пирса. MIT Press.
- Заламеа, Фернандо. Логика непрерывности Пирса. Docent Press, Бостон, Массачусетс. 2012. ISBN 9 780983 700494.
- Часть II: Экзистенциальные графы Пирса, стр. 76-162.
- Земан, Дж. Дж.
- (1964), Графическая логика К.С. Пирса. Неопубликованная докторская степень. диссертация представлена в Чикагский университет.
- (1967), «Система неявной количественной оценки», Журнал символической логики 32: 480–504.
внешняя ссылка
- Стэнфордская энциклопедия философии: Логика Пирса Сун-Джу Шин и Эрик Хаммер.
- Дау, Фритьоф, Экзистенциальные графики Пирса --- чтения и ссылки. Аннотированная библиография по экзистенциальным графам.
- Готчалл, Кристиан, Proof Builder - Java-апплет для построения альфа-графиков.
- Лю Синь-Вэнь "Литература по экзистенциальным графам К.С.Пирса "(через Wayback Machine), Институт философии Китайской академии социальных наук, Пекин, КНР.
- Сова, Джон Ф. «Законы, факты и контексты: основы мультимодального мышления». Получено 2009-10-23. (NB. Экзистенциальные графы и концептуальные графики.)
- Ван Хёвельн, Брэм "Экзистенциальные графы. "Отделение когнитивных наук, Политехнический институт Ренсселера. Только альфа.
- Земан, Джей Дж. "Экзистенциальные графы ". С четыре онлайн-статьи пользователя Peirce.
