Экваториальная выпуклость - Equatorial bulge

Для функции на некоторых из Сатурн луны, смотри экваториальный гребень.

An экваториальная выпуклость разница между экваториальный и полярный диаметры из планета, из-за центробежная сила осуществляется вращение по оси тела. Вращающееся тело имеет тенденцию образовывать сплюснутый сфероид а не сфера.

На земле

Основная статья: Фигура Земли

В земной шар имеет довольно небольшую экваториальную выпуклость: на экваторе она примерно на 43 км (27 миль) шире, чем расстояние от полюса до полюса, разница составляет около 1/300 диаметра. Если бы Землю уменьшить в масштабе до шара диаметром 1 метр на экваторе, разница составила бы всего 3 миллиметра. Хотя эта разница слишком мала, чтобы ее можно было заметить визуально, это все же более чем в два раза превышает самые большие отклонения реальной поверхности от эллипсоида, включая самые высокие горы и самые глубокие океанические впадины.

Вращение Земли также влияет на уровень моря, воображаемая поверхность, которая используется для измерения высоты из. Эта поверхность совпадает со средним уровнем поверхности воды в океанах и экстраполируется на сушу с учетом местного гравитационный потенциал и центробежная сила.

Разница в радиусы Таким образом, около 21 км. Наблюдатель, стоящий на уровне моря столб, следовательно, находится на 21 км ближе к центру Земли, чем если бы она стояла на уровне моря на экваторе. В результате самая высокая точка на Земле, измеренная от центра и наружу, является вершиной горы. Чимборасо в Эквадор скорее, чем гора Эверест. Но поскольку океан тоже выпирает, как Земля и его атмосфера, Чимборасо не так высоко над уровнем моря, как Эверест.

Точнее, поверхность земной шар обычно аппроксимируется идеалом сплюснутый эллипсоид, для точного определения широта и долгота сетка для картография, а также «центр Земли». в WGS-84 стандарт Эллипсоид Земли, широко используется для картографии и GPS системы радиус Земли предполагается равным 6378.137 км (3963.191 mi) на экваторе и 6356.7523142 км (3949.9027642 ми) межполюсный; имея в виду разницу 21.3846858 км (13.2878277 mi) по радиусам и 42.7693716 км (26.5756554 mi) в диаметрах, а относительный сплющивание из 1 / 298.257223563. Поверхность уровня моря намного ближе к этому стандартному эллипсоиду, чем поверхность твердой Земли.

Равновесие как баланс энергий

К вертикальному стержню прикреплена пружинная металлическая лента. В неподвижном состоянии металлическая полоса пружины имеет круглую форму. Верх металлической ленты может скользить по вертикальной штанге. При вращении пружинно-металлическая полоса выпирает на экваторе и сглаживается на полюсах по аналогии с Землей.

Сила тяжести имеет тенденцию сжимать небесное тело в сфера, форма, для которой вся масса находится как можно ближе к центру тяжести. Вращение вызывает искажение этой сферической формы; распространенной мерой искажения является сплющивание (иногда называемая эллиптичностью или сплющенностью), которая может зависеть от множества факторов, включая размер, угловая скорость, плотность, и эластичность.

Чтобы почувствовать тип равновесия, представьте себе человека, сидящего на вращающемся стуле с гирями в руках. Если человек в кресле тянет к себе гири, он выполняет работу, и его кинетическая энергия вращения увеличивается. Увеличение скорости вращения настолько велико, что при более высокой скорости вращения требуется центростремительная сила больше, чем при начальной скорости вращения.

Нечто подобное происходит при формировании планет. Материя сначала сливается в медленно вращающееся дискообразное распределение, а столкновения и трение преобразуют кинетическую энергию в тепло, что позволяет диску самогравитировать в очень сжатый сфероид.

Пока протопланета все еще слишком сплюснута, чтобы находиться в равновесии, высвобождение гравитационной потенциальной энергии при сжатии продолжает приводить к увеличению вращательной кинетической энергии. По мере того как сжатие продолжается, скорость вращения продолжает расти, следовательно, сила, необходимая для дальнейшего сжатия, продолжает расти. Есть точка, в которой увеличение вращательной кинетической энергии при дальнейшем сокращении будет больше, чем высвобождение гравитационной потенциальной энергии. Процесс сжатия может продолжаться только до этого момента, поэтому он останавливается там.

Пока нет равновесия, может происходить сильная конвекция, а пока существует сильная конвекция, трение может преобразовывать кинетическую энергию в тепло, высасывая кинетическую энергию вращения из системы. Когда состояние равновесия достигнуто, крупномасштабное преобразование кинетической энергии в тепло прекращается. В этом смысле состояние равновесия - это самое низкое энергетическое состояние, которое может быть достигнуто.

Скорость вращения Земли все еще замедляется, хотя и постепенно, примерно на две тысячных секунды за оборот каждые 100 лет.^[1] Оценки того, насколько быстро Земля вращалась в прошлом, различаются, потому что точно не известно, как образовалась Луна. По оценкам, вращение Земли 500 миллионов лет назад составляет около 20 современных часов в «день».

Скорость вращения Земли замедляется в основном из-за приливных взаимодействий с Луной и Солнцем. Поскольку твердые части Земли пластичный экваториальная выпуклость Земли уменьшалась одновременно с уменьшением скорости вращения.

Различия в ускорении свободного падения

Силы, действующие в случае планеты с экваториальной выпуклостью из-за вращения.
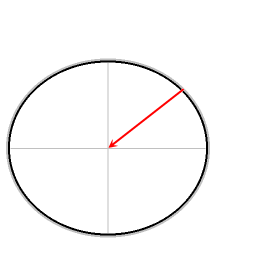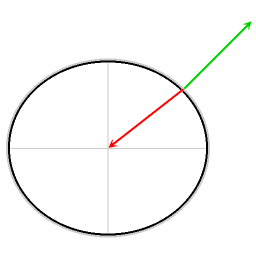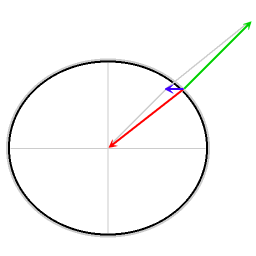
Красная стрелка: гравитация
Зеленая стрелка, нормальная сила
Синяя стрелка: результирующая сила

Результирующая сила обеспечивает необходимую центростремительную силу. Без этой центростремительной силы объекты без трения скользили бы к экватору.

В расчетах, когда используется система координат, вращающаяся вместе с Землей, вектор условного центробежная сила направлен наружу и такой же большой, как вектор, представляющий центростремительную силу.

Из-за вращения планеты вокруг своей оси гравитационное ускорение меньше на экваторе, чем на полюсах. В 17 веке, после изобретения маятниковые часы, Французские ученые обнаружили, что часы, отправленные в Французская Гвиана, на северном побережье Южная Америка, работали медленнее, чем их аналоги в Париже. При измерении ускорения свободного падения на экваторе также необходимо учитывать вращение планеты. Любой объект, который неподвижен по отношению к поверхности Земли, на самом деле следует по круговой траектории, огибая ось Земли. Чтобы вывести объект по такой круговой траектории, требуется сила. Ускорение, необходимое для обхода оси Земли вдоль экватора со скоростью один оборот за звездный день составляет 0,0339 м / с². Обеспечение этого ускорения снижает эффективное ускорение свободного падения. На экваторе эффективное ускорение свободного падения составляет 9,7805 м / с.². Это означает, что истинное ускорение свободного падения на экваторе должно составлять 9,8144 м / с.² (9.7805 + 0.0339 = 9.8144).

На полюсах ускорение свободного падения 9,8322 м / с.². Разница 0,0178 м / с² Между ускорением свободного падения на полюсах и истинным ускорением свободного падения на экваторе объясняется тем, что объекты, расположенные на экваторе, примерно на 21 километр дальше от центра масс Земли, чем на полюсах, что соответствует меньшему ускорению свободного падения.

Итак, есть два вклада в тот факт, что эффективное гравитационное ускорение на экваторе меньше, чем на полюсах. Около 70 процентов разницы связано с тем, что объекты движутся вокруг оси Земли, а около 30 процентов связано с несферической формой Земли.

Диаграмма показывает, что на всех широтах эффективное ускорение свободного падения уменьшается из-за требования обеспечения центростремительной силы; убывающий эффект сильнее всего на экваторе.

Влияние на орбиты спутников

Тот факт, что гравитационное поле Земли незначительно отклоняется от сферической симметрии, также влияет на орбиты спутники через светский орбитальные прецессии.^[2][3][4] Они зависят от ориентации оси симметрии Земли в инерциальном пространстве и в общем случае влияют на все кеплеровский орбитальные элементы за исключением большая полуось. Если ссылка z ось принятой системы координат совмещена с осью симметрии Земли, тогда только долгота восходящего узла Ω, то аргумент перицентра ω и средняя аномалия M претерпевают вековые прецессии.^[5]

Такие возмущения, которые ранее использовались для картографирования гравитационного поля Земли из космоса,^[6] может играть важную тревожную роль, когда спутники используются для тестирования общая теория относительности^[7] потому что гораздо меньшие релятивистские эффекты качественно неотличимы от возмущений, вызванных сжатием.

Формулировка

Коэффициент сплющивания ${\displaystyle f}$ для равновесной конфигурации самогравитирующего сфероида, состоящего из несжимаемой жидкости с однородной плотностью, устойчиво вращающегося вокруг некоторой фиксированной оси, при небольшом сжатии, аппроксимируется следующим образом:^[8]

${\displaystyle f={\frac {a_{e}-a_{p}}{a}}={\frac {5}{4}}{\frac {\omega ^{2}a^{3}}{GM}}={\frac {15\pi }{4}}{\frac {1}{GT^{2}\rho }}}$

куда

${\displaystyle G}$ универсальный гравитационная постоянная,

${\displaystyle a}$ - средний радиус,

${\displaystyle a_{e}=a\,(1+{\tfrac {f}{3}})}$ и ${\displaystyle a_{p}=a\,(1-{\tfrac {2f}{3}})}$ - соответственно экваториальный и полярный радиус,

${\displaystyle T}$ - период вращения и ${\displaystyle \omega ={\tfrac {2\pi }{T}}}$ это угловая скорость,

${\displaystyle \rho }$ это плотность тела и ${\displaystyle M\simeq {\tfrac {4}{3}}\pi \rho a^{3}}$ это общая масса тела.

Реальное сплющивание меньше из-за концентрации массы в центре небесных тел.

Другие небесные тела

Смотрите также: Справочный эллипсоид § Другие небесные тела

Экваториальная выпуклость главных небесных тел Солнечной системы

Тело	Диаметр (км)		Экваториальный выпуклость (км)	Сплющивание соотношение	Вращение период (ч)	Плотность (кг / м^3)	${\displaystyle f}$	Отклонение из ${\displaystyle f}$
	Экваториальный	Полярный
земной шар	012 756.2	012 713.6	00 042.6	1 : 299.4	23.936	5515	1 : 232	−23%
Марс	006 792.4	006 752.4	00 040	1 : 170	24.632	3933	1 : 175	0+3%
Церера	000 964.3	000 891.8	00072.5	1 : 13.3	09.074	2162	1 : 13.1	0−2%
Юпитер	142 984	133 708	09 276	1 : 15.41	09.925	1326	1 : 9.59	−38%
Сатурн	120 536	108 728	11 808	1 : 10.21	10.56	0687	1 : 5.62	−45%
Уран	051 118	049 946	01 172	1 : 43.62	17.24	1270	1 : 27.71	−36%
Нептун	049 528	048 682	00 846	1 : 58.54	16.11	1638	1 : 31.22	−47%

Как правило, любое вращающееся небесное тело (достаточно массивное, чтобы принять сферическую или почти сферическую форму) будет иметь экваториальную выпуклость, соответствующую скорости его вращения. С 11808 км Сатурн - планета с самой большой экваториальной выпуклостью в нашей Солнечной системе. Экваториальные выпуклости не следует путать с экваториальные гребни. Экваториальные гребни характерны как минимум для четырех спутников Сатурна: большой спутник Япет и крошечные луны Атлас, Сковорода, и Дафнис. Эти хребты близко следуют за экваторами лун. Гребни кажутся уникальными для системы Сатурна, но неясно, связаны ли эти явления или они являются совпадением. Первые три были обнаружены Кассини зонд в 2005 году; Дафнейский хребет был открыт в 2017 году. Хребет на Япете имеет ширину около 20 км, высоту 13 км и длину 1300 км. Гребень на Атласе пропорционально еще более примечателен, учитывая гораздо меньший размер Луны, что придает ей дискообразную форму. Изображения Пана показывают структуру, аналогичную структуре Атласа, в то время как изображение на Дафнисе менее выражено.

Рекомендации

1. Хадхази, Адам. «Факт или вымысел: дни (и ночи) становятся длиннее». Scientific American. Получено 5 декабря 2011.
2. Иорио, Л. (2011). «Возмущенные движения звезд вокруг вращающейся черной дыры в Sgr A * для общей ориентации ее оси вращения». Физический обзор D. 84 (12): 124001. arXiv:1107.2916. Bibcode:2011ПхРвД..84л4001И. Дои:10.1103 / PhysRevD.84.124001.
3. Рензетти, Г. (2013). «Прецессии орбиты спутников, вызванные октуполярным моментом массы несферического тела, произвольно ориентированного в пространстве». Журнал астрофизики и астрономии. 34 (4): 341–348. Bibcode:2013JApA ... 34..341R. Дои:10.1007 / s12036-013-9186-4.
4. Рензетти, Г. (2014). «Прецессии орбиты спутников, вызванные первым нечетным зональным мультиполем J3 несферического тела, произвольно ориентированного в пространстве». Астрофизика и космическая наука. 352 (2): 493–496. Bibcode:2014Ap и SS.352..493R. Дои:10.1007 / s10509-014-1915-х.
5. Кинг-Хеле, Д. Г. (1961). «Гравитационный потенциал Земли, рассчитанный по орбитам искусственных спутников». Геофизический журнал. 4 (1): 3–16. Bibcode:1961GeoJ .... 4 .... 3K. Дои:10.1111 / j.1365-246X.1961.tb06801.x.
6. Кинг-Хеле, Д. Г. (1983). «Геофизические исследования с орбитами первых спутников». Геофизический журнал. 74 (1): 7–23. Bibcode:1983GeoJ ... 74 .... 7K. Дои:10.1111 / j.1365-246X.1983.tb01868.x.
7. Рензетти, Г. (2012). «Действительно ли даже зональные более высокой степени вредны для эксперимента с перетаскиванием кадра LARES / LAGEOS?». Канадский журнал физики. 90 (9): 883–888. Bibcode:2012CaJPh..90..883R. Дои:10.1139 / p2012-081.
8. «Вращательное сплющивание». utexas.edu.