Уравнение Эмдена – Чандрасекара - Emden–Chandrasekhar equation

Численное решение уравнения Эмдена – Чандрасекара.

В астрофизика, то Уравнение Эмдена – Чандрасекара это безразмерный форма Уравнение Пуассона для распределения плотности сферически симметричной изотермический газовый шар, подверженный действию собственной гравитационной силы, названный Роберт Эмден и Субраманян Чандрасекар.^[1][2] Уравнение было впервые введено Роберт Эмден в 1907 г.^[3] Уравнение^[4] читает

${\displaystyle {\frac {1}{\xi ^{2}}}{\frac {d}{d\xi }}\left(\xi ^{2}{\frac {d\psi }{d\xi }}\right)=e^{-\psi }}$

куда ${\displaystyle \xi }$ - безразмерный радиус, а ${\displaystyle \psi }$ связана с плотностью газовой сферы как ${\displaystyle \rho =\rho _{c}e^{-\psi }}$, куда ${\displaystyle \rho _{c}}$ - плотность газа в центре. Уравнение не имеет известного явного решения. Если политропный жидкость используется вместо изотермической жидкости, получается Уравнение Лейна – Эмдена. Изотермическое предположение обычно моделируется для описания ядра звезды. Уравнение решается с начальными условиями,

${\displaystyle \psi =0,\quad {\frac {d\psi }{d\xi }}=0\quad {\text{at}}\quad \xi =0.}$

Уравнение появляется и в других разделах физики, например, такое же уравнение появляется в Теория взрыва Франк-Каменецкого для сферического сосуда. Релятивистская версия этой сферически-симметричной изотермической модели была изучена Субраманяном Чандрасекаром в 1972 году.^[5]

Вывод

Для изотермический газообразный звезда, давление ${\displaystyle p}$ связано с кинетической давление и радиационное давление

${\displaystyle p=\rho {\frac {k_{B}}{WH}}T+{\frac {4\sigma }{3c}}T^{4}}$

куда

• ${\displaystyle \rho }$ это плотность
• ${\displaystyle k_{B}}$ это Постоянная Больцмана
• ${\displaystyle W}$ это среднее молекулярный вес
• ${\displaystyle H}$ это масса протона
• ${\displaystyle T}$ это температура звезды
• ${\displaystyle \sigma }$ это Постоянная Стефана – Больцмана
• ${\displaystyle c}$ это скорость света

Уравнение равновесия звезды требует баланса между силой давления и силой тяжести.

${\displaystyle {\frac {1}{r^{2}}}{\frac {d}{dr}}\left({\frac {r^{2}}{\rho }}{\frac {dp}{dr}}\right)=-4\pi G\rho }$

куда ${\displaystyle r}$ - радиус, отсчитываемый от центра, а ${\displaystyle G}$ это гравитационная постоянная. Уравнение переписывается как

${\displaystyle {\frac {k_{B}T}{WH}}{\frac {1}{r^{2}}}{\frac {d}{dr}}\left(r^{2}{\frac {d\ln \rho }{dr}}\right)=-4\pi G\rho }$

Фактическое решение и асимптотическое решение

Представляем трансформацию

${\displaystyle \psi =\ln {\frac {\rho _{c}}{\rho }},\quad \xi =r\left({\frac {4\pi G\rho _{c}WH}{k_{B}T}}\right)^{1/2}}$

куда ${\displaystyle \rho _{c}}$ - центральная плотность звезды, приводит к

${\displaystyle {\frac {1}{\xi ^{2}}}{\frac {d}{d\xi }}\left(\xi ^{2}{\frac {d\psi }{d\xi }}\right)=e^{-\psi }}$

Граничные условия:

${\displaystyle \psi =0,\quad {\frac {d\psi }{d\xi }}=0\quad {\text{at}}\quad \xi =0}$

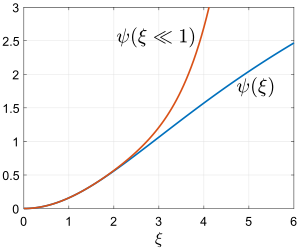
За ${\displaystyle \xi \ll 1}$, решение выглядит как

${\displaystyle \psi ={\frac {\xi ^{2}}{6}}-{\frac {\xi ^{4}}{120}}+{\frac {\xi ^{6}}{1890}}+\cdots }$

Ограничения модели

Предположение изотермической сферы имеет некоторые недостатки. Хотя плотность, полученная в результате растворения этой изотермической газовой сферы, уменьшается от центра, она уменьшается слишком медленно, чтобы получить четко определенную поверхность и конечную массу для сферы. Можно показать, что при ${\displaystyle \xi \gg 1}$,

${\displaystyle {\frac {\rho }{\rho _{c}}}=e^{-\psi }={\frac {2}{\xi ^{2}}}\left[1+{\frac {A}{\xi ^{1/2}}}\cos \left({\frac {\sqrt {7}}{2}}\ln \xi +\delta \right)+O(\xi ^{-1})\right]}$

куда ${\displaystyle A}$ и ${\displaystyle \delta }$ - константы, которые будут получены численным решением. Такое поведение плотности приводит к увеличению массы с увеличением радиуса. Таким образом, модель обычно пригодна для описания ядра звезды, где температура примерно постоянна.^[6]

Уникальное решение

Представляем трансформацию ${\displaystyle x=1/\xi }$ преобразует уравнение к

${\displaystyle x^{4}{\frac {d^{2}\psi }{dx^{2}}}=e^{-\psi }}$

Уравнение имеет единственное решение данный

${\displaystyle e^{-\psi _{s}}=2x^{2},\quad {\text{or}}\quad -\psi _{s}=2\ln x+\ln 2}$

Следовательно, новую переменную можно ввести как ${\displaystyle -\psi =2\ln x+z}$, где уравнение для ${\displaystyle z}$ можно вывести,

${\displaystyle {\frac {d^{2}z}{dt^{2}}}-{\frac {dz}{dt}}+e^{z}-2=0,\quad {\text{where}}\quad t=\ln x}$

Это уравнение можно свести к первому порядку, введя

${\displaystyle y={\frac {dz}{dt}}=\xi {\frac {d\psi }{d\xi }}-2}$

тогда у нас есть

${\displaystyle y{\frac {dy}{dz}}-y+e^{z}-2=0}$

Снижение

Есть еще одно сокращение из-за Эдвард Артур Милн. Определим

${\displaystyle u={\frac {\xi e^{-\psi }}{d\psi /d\xi }},\quad v=\xi {\frac {d\psi }{d\xi }}}$

тогда

${\displaystyle {\frac {u}{v}}{\frac {dv}{du}}={\frac {u-1}{u+v-3}}}$

Характеристики

• Если ${\displaystyle \psi (\xi )}$ является решением уравнения Эмдена – Чандрасекара, то ${\displaystyle \psi (A\xi )-2\ln A}$ также является решением уравнения, где ${\displaystyle A}$ - произвольная постоянная.
• Конечные в начале координат решения уравнения Эмдена – Чандрасекара обязательно должны иметь ${\displaystyle d\psi /d\xi =0}$ в ${\displaystyle \xi =0}$

Смотрите также

• Уравнение Лейна – Эмдена
• Теория Франк-Каменецкого
• Уравнение белого карлика Чандрасекара

Рекомендации

1. Чандрасекар, Субрахманян и Субраманян Чандрасекар. Введение в изучение звездного строения. Vol. 2. Курьерская корпорация, 1958 год.
2. Чандрасекхар С. и Гордон В. Уэрс. «Изотермическая функция». Астрофизический журнал 109 (1949): 551-554.http://articles.adsabs.harvard.edu/cgi-bin/nph-iarticle_query?1949ApJ...109..551C&defaultprint=YES&filetype=.pdf
3. Эмден, Р. (1907). Gaskugeln: Anwendungen der Mechanischen Wärmetheorie auf kosmologische und meteorologische Probleme. Б. Тойбнер ..
4. Киппенхан, Рудольф, Альфред Вейгерт и Ахим Вайс. Звездное строение и эволюция. Vol. 282. Берлин: Springer-Verlag, 1990.
5. Чандрасекхар, С. (1972). Предельный случай релятивистского равновесия. В общей теории относительности (в честь Дж. Л. Синге), изд. Л. О'Рейфартей. Оксфорд. Кларендон Пресс (стр 185-199).
6. Генрих, Л. Р., и Чандрасекхар, С. (1941). Звездные модели с изотермическими ядрами. Астрофизический журнал, 94, 525.