Электрическая восприимчивость - Electric susceptibility

В электричестве (электромагнетизм ), электрическая восприимчивость (${\displaystyle \chi _{\text{e}}}$; латинский: восприимчивый "восприимчивый") - безразмерная константа пропорциональности, указывающая степень поляризация из диэлектрик материал в ответ на нанесенный электрическое поле. Чем больше электрическая восприимчивость, тем больше способность материала поляризоваться в ответ на поле и тем самым уменьшать общее электрическое поле внутри материала (и накапливать энергию). Таким образом, электрическая восприимчивость влияет на электрическую диэлектрическая проницаемость материала и, таким образом, влияет на многие другие явления в этой среде из-за емкости конденсаторы к скорость света.^[1][2]

Определение электрической восприимчивости

Электрическая восприимчивость определяется как константа пропорциональности (которая может быть матрицей), относящаяся к электрическое поле E к индуцированному диэлектрик плотность поляризации п такой, что:

${\displaystyle {\mathbf {P} }=\varepsilon _{0}\chi _{\text{e}}{\mathbf {E} },}$

куда

• ${\displaystyle \mathbf {P} }$ - плотность поляризации;
• ${\displaystyle \varepsilon _{0}}$ это электрическая проницаемость свободного пространства (электрическая постоянная);
• ${\displaystyle \chi _{\text{e}}}$ электрическая восприимчивость;
• ${\displaystyle \mathbf {E} }$ - электрическое поле.

Восприимчивость связана с его относительная диэлектрическая проницаемость (диэлектрическая постоянная) ${\displaystyle \varepsilon _{\textrm {r}}}$ к:

${\displaystyle \chi _{\text{e}}\ =\varepsilon _{\text{r}}-1}$

Итак, в случае с вакуумом:

${\displaystyle \chi _{\text{e}}\ =0}$

В то же время электрическое перемещение D связана с плотностью поляризации п к:

${\displaystyle \mathbf {D} \ =\ \varepsilon _{0}\mathbf {E} +\mathbf {P} \ =\ \varepsilon _{0}(1+\chi _{\text{e}})\mathbf {E} \ =\ \varepsilon _{\text{r}}\varepsilon _{0}\mathbf {E} \ =\ \varepsilon \mathbf {E} .}$

Где

• ${\displaystyle \varepsilon \ =\ \varepsilon _{\text{r}}\varepsilon _{0}}$
• ${\displaystyle \varepsilon _{\text{r}}\ =\ (1+\chi _{\text{e}})}$

Молекулярная поляризуемость

Аналогичный параметр существует, чтобы связать величину индуцированного дипольный момент п индивидуального молекула к местному электрическому полю E что вызвало диполь. Этот параметр является молекулярная поляризуемость (α), и дипольный момент, возникающий из-за локального электрического поля E_{местный} дан кем-то:

${\displaystyle \mathbf {p} =\varepsilon _{0}\alpha \mathbf {E_{\text{local}}} }$

Однако это вносит сложности, поскольку локально поле может значительно отличаться от общего приложенного поля. У нас есть:

${\displaystyle \mathbf {P} =N\mathbf {p} =N\varepsilon _{0}\alpha \mathbf {E} _{\text{local}},}$

куда п - поляризация на единицу объема, а N - количество молекул в единице объема, вносящих вклад в поляризацию. Таким образом, если локальное электрическое поле параллельно окружающему электрическому полю, мы имеем:

${\displaystyle \chi _{\text{e}}\mathbf {E} =N\alpha \mathbf {E} _{\text{local}}}$

Таким образом, только если локальное поле равно окружающему полю, мы можем написать:

${\displaystyle \chi _{\text{e}}=N\alpha .}$

В противном случае следует найти связь между локальным и макроскопическим полем. В некоторых материалах Соотношение Клаузиуса – Моссотти держит и читает

${\displaystyle {\frac {\chi _{\text{e}}}{3+\chi _{\text{e}}}}={\frac {N\alpha }{3}}.}$

Неопределенность в определении

Определение молекулярной поляризуемости зависит от автора. В приведенном выше определении

${\displaystyle \mathbf {p} =\varepsilon _{0}\alpha \mathbf {E_{\text{local}}} ,}$

${\displaystyle p}$ и ${\displaystyle E}$ в единицах СИ, а поляризуемость молекул ${\displaystyle \alpha }$ имеет размерность объема (м³). Другое определение^[3] было бы сохранить единицы СИ и интегрировать ${\displaystyle \varepsilon _{0}}$ в ${\displaystyle \alpha }$:

${\displaystyle \mathbf {p} =\alpha \mathbf {E_{\text{local}}} .}$

В этом втором определении поляризуемость будет иметь единицу СИ - К. м.²/ V. Существует еще одно определение^[4] куда ${\displaystyle p}$ и ${\displaystyle E}$ выражаются в системе cgs и ${\displaystyle \alpha }$ все еще определяется как

${\displaystyle \mathbf {p} =\alpha \mathbf {E_{\text{local}}} .}$

С использованием единицы cgs дает ${\displaystyle \alpha }$ размер тома, как в первом определении, но со значением, которое ${\displaystyle 4\pi }$ ниже.

Нелинейная восприимчивость

Во многих материалах поляризуемость начинает насыщаться при высоких значениях электрического поля. Это насыщение можно смоделировать с помощью нелинейная восприимчивость. Эти восприимчивости важны для нелинейная оптика и приводят к таким эффектам, как генерация второй гармоники (например, используется для преобразования инфракрасного света в видимый, зеленый лазерные указки ).

Стандартное определение нелинейной восприимчивости в единицах СИ - через Расширение Тейлора реакции поляризации на электрическое поле:^[5]

${\displaystyle P=P_{0}+\varepsilon _{0}\chi ^{(1)}E+\varepsilon _{0}\chi ^{(2)}E^{2}+\varepsilon _{0}\chi ^{(3)}E^{3}+\cdots .}$

(За исключением сегнетоэлектрик материалы, встроенная поляризация нулевая, ${\displaystyle P_{0}=0}$.) Первый член восприимчивости, ${\displaystyle \chi ^{(1)}}$, соответствует описанной выше линейной восприимчивости. Хотя это первое слагаемое безразмерно, последующие нелинейные восприимчивости ${\displaystyle \chi ^{(n)}}$ иметь единицы (м / В)^п-1.

Нелинейные восприимчивости можно обобщить до анизотропный материалы, восприимчивость которых неоднородна во всех направлениях. В этих материалах каждая восприимчивость ${\displaystyle \chi ^{(n)}}$ становится п + 1-классифицировать тензор.

Дисперсия и причинность

Схематический график диэлектрической проницаемости как функции частоты света, показывающий несколько резонансов и плато, указывающих на активацию определенных процессов, которые могут реагировать на возмущение во временных масштабах частоты света. Это демонстрирует, что размышление о восприимчивости в терминах ее преобразования Фурье полезно, поскольку свет - это возмущение с постоянной частотой для материала.

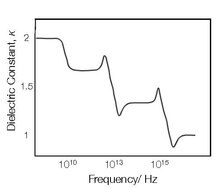
В общем, материал не может поляризоваться мгновенно в ответ на приложенное поле, поэтому более общая формулировка как функция времени такова:

${\displaystyle \mathbf {P} (t)=\varepsilon _{0}\int _{-\infty }^{t}\chi _{\text{e}}(t-t')\mathbf {E} (t')\,\mathrm {d} t'.}$

То есть поляризация свертка электрического поля в предыдущие моменты времени с зависимой от времени восприимчивостью, определяемой ${\displaystyle \chi _{\text{e}}(\Delta t)}$. Верхний предел этого интеграла можно продолжить до бесконечности, если определить ${\displaystyle \chi _{\text{e}}(\Delta t)=0}$ за ${\displaystyle \Delta t<0}$. Мгновенный ответ соответствует Дельта-функция Дирака восприимчивость ${\displaystyle \chi _{\text{e}}(\Delta t)=\chi _{\text{e}}\delta (\Delta t)}$.

В линейной системе удобнее брать преобразование Фурье и запишите это отношение как функцию частоты. Из-за теорема свертки, интеграл становится произведением,

${\displaystyle \mathbf {P} (\omega )=\varepsilon _{0}\chi _{\text{e}}(\omega )\mathbf {E} (\omega ).}$

Эта частотная зависимость восприимчивости приводит к частотной зависимости диэлектрической проницаемости. Форма восприимчивости по частоте характеризует разброс свойства материала.

Более того, тот факт, что поляризация может зависеть только от электрического поля в предыдущие моменты времени (т.е. ${\displaystyle \chi _{\text{e}}(\Delta t)=0}$ за ${\displaystyle \Delta t<0}$), как следствие причинность, навязывает Ограничения Крамерса – Кронига на восприимчивость ${\displaystyle \chi _{\text{e}}(0)}$.

Смотрите также

• Применение тензорной теории в физике
• Магнитная восприимчивость
• Уравнения Максвелла
• Разрешающая способность
• Соотношение Клаузиуса-Моссотти
• Функция линейного отклика
• Отношения Грина – Кубо

Рекомендации

1. «Электрическая восприимчивость». Британская энциклопедия.
2. Кардарелли, Франсуа (2000–2008). Справочник по материалам: краткий настольный справочник (2-е изд.). Лондон: Springer-Verlag. с. 524 (Раздел 8.1.16). Дои:10.1007/978-1-84628-669-8. ISBN  978-1-84628-668-1.
3. CRC Справочник по химии и физике (PDF) (84-е изд.). CRC. С. 10–163. Архивировано из оригинал (PDF) на 2016-10-06. Получено 2016-08-19.
4. CRC Справочник по химии и физике (PDF) (84-е изд.). CRC. С. 10–163. Архивировано из оригинал (PDF) на 2016-10-06. Получено 2016-08-19.
5. Пол Н. Бутчер, Дэвид Коттер, Элементы нелинейной оптики