Комплекс Кокстера - Coxeter complex

В математике Комплекс Кокстера, названный в честь Х. С. М. Коксетер, - геометрическая конструкция (a симплициальный комплекс ) связанный с Группа Коксетера. Комплексы Кокстера - основные объекты, позволяющие возводить здания; они образуют квартиры дома.

Строительство

Каноническое линейное представление

Первый ингредиент в строительстве комплекса Кокстера, связанный с группой Кокстера. W это определенный представление из W, называемый каноническим представлением W.

Позволять ${\displaystyle (W,S)}$ быть Система Кокстера связано с W, с Матрица Кокстера ${\displaystyle M=(m(s,t))_{s,t\in S}}$. Каноническое представление задается векторным пространством V на основе формальных символов ${\displaystyle (e_{s})_{s\in S}}$, который наделен симметричной билинейной формой ${\displaystyle B(e_{s},e_{t})=-\cos \left({\frac {\pi }{m(s,t)}}\right)}$. Действие W на этом векторном пространстве V тогда дается ${\displaystyle s(v)=v-2{\frac {B(e_{s},v)}{B(e_{s},e_{s})}}e_{s}}$, как мотивировано выражением для отражений в корневые системы.

Это представление имеет несколько фундаментальных свойств в теории групп Кокстера; например, билинейная форма B положительно определен тогда и только тогда, когда W конечно. Это (всегда) верное представление из W.

Камеры и конус Титца

Можно думать об этом представлении как о выражении W как своего рода группа отражения, с оговоркой, что B не может быть положительно определенным. Тогда становится важным различать представление V от его двойного V^*. Векторы ${\displaystyle e_{s}}$ роды V, и имеют соответствующие двойственные векторы ${\displaystyle e_{s}^{\vee }}$ в V^*, предоставленный:

${\displaystyle \langle e_{s}^{\vee },v\rangle =2{\frac {B(e_{s},v)}{B(e_{s},e_{s})}},}$

где угловые скобки указывают на естественное спаривание двойственного вектора в V^* с вектором V, и B является билинейной формой, как указано выше.

Сейчас же W действует на V^*, а действие удовлетворяет формуле

${\displaystyle s(f)=f-\langle f,e_{s}\rangle e_{s}^{\vee },}$

за ${\displaystyle s\in S}$ и любой ж в V^*. Это выражает s как отражение в гиперплоскости ${\displaystyle H_{s}=\{f\in V^{*}:\langle f,e_{s}\rangle =0\}}$. У одного есть основная камера ${\displaystyle {\mathcal {C}}=\{f\in V^{*}:\langle f,e_{s}\rangle >0\ \forall s\in S\}}$, это имеет лица так называемые стены, ${\displaystyle H_{s}}$. Остальные камеры можно получить из ${\displaystyle {\mathcal {C}}}$ переводом: они ${\displaystyle w{\mathcal {C}}}$ за ${\displaystyle w\in W}$.

Учитывая фундаментальную камеру ${\displaystyle {\mathcal {C}}}$, то Конус сисек определяется как ${\displaystyle X=\bigcup _{w\in W}w{\overline {\mathcal {C}}}}$. Это не обязательно должно быть все V^*. Очень важно то, что конус Титса Икс выпуклый. Действие W на конусе синицы Икс имеет фундаментальная область основная палата ${\displaystyle {\mathcal {C}}}$.

Комплекс Кокстера

После определения конуса Титса Икс, комплекс Кокстера ${\displaystyle \Sigma (W,S)}$ из W относительно S можно определить как частное от Икс, с удаленным источником, положительные реалы (ℝ⁺, ×):

${\displaystyle \Sigma (W,S)=(X\setminus \{0\})/\mathbb {R} ^{+}}$.

Примеры

Конечные диэдральные группы

В диэдральные группы ${\displaystyle D_{n}}$ (порядка 2п) - группы Кокстера соответствующего типа ${\displaystyle \mathrm {I} _{2}(n)}$. У них есть презентация ${\displaystyle \left\langle s,t\,\left|\,s^{2},t^{2},(st)^{n}\right\rangle \right.}$.

Каноническое линейное представление ${\displaystyle \mathrm {I} _{2}(n)}$ является обычным отражательным представлением группы диэдра, действующим на п-угольник в плоскости (так ${\displaystyle V=\mathbb {R} ^{2}}$ в этом случае). Например, в случае п = 3, получаем группу Кокстера типа ${\displaystyle \mathrm {I} _{2}(3)=\mathrm {A} _{2}}$, действующий на равносторонний треугольник на плоскости. Каждое отражение s имеет связанную гиперплоскость ЧАС_s в двойственном векторном пространстве (которое может быть канонически отождествлено с самим векторным пространством, используя билинейную форму B, который в данном случае является внутренним продуктом, как отмечалось выше), это стены. Они вырезают камеры, как показано ниже:

Тогда комплекс Кокстера - это соответствующие 2п-gon, как на изображении выше. Это симплициальный комплекс размерности 1, его можно раскрасить по котипу.

Бесконечная диэдральная группа

Еще один мотивирующий пример - это бесконечная диэдральная группа ${\displaystyle D_{\infty }}$. Это можно рассматривать как группу симметрий реальной прямой, которая сохраняет набор точек с целыми координатами; он создается отражениями в ${\displaystyle x=0}$ и ${\displaystyle x={1 \over 2}}$. У этой группы есть презентация Кокстера ${\displaystyle \left\langle s,t\,\left|\,s^{2},t^{2}\right\rangle \right.}$.

В этом случае идентифицировать уже невозможно V с двойным пространством V^*, так как B не является положительно определенным. Тогда лучше работать только с V^*, где и определены гиперплоскости. Это дает следующую картину:

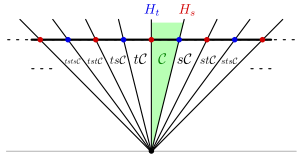
В этом случае конус Титса - это не вся плоскость, а только верхняя полуплоскость. Выравнивание по положительным числам дает еще одну копию реальной линии с отмеченными точками у целых чисел. Это комплекс Кокстера бесконечной диэдральной группы.

Альтернативное строительство комплекса Coxeter

Другое описание комплекса Кокстера использует стандартные смежные классы группы Кокстера. W. Стандартный смежный класс - это смежный класс вида ${\displaystyle wW_{J}}$, куда ${\displaystyle W_{J}=\langle J\rangle }$ для некоторого подмножества J из S. Например, ${\displaystyle W_{S}=W}$ и ${\displaystyle W_{\emptyset }=\{1\}}$.

Комплекс Кокстера ${\displaystyle \Sigma (W,S)}$ тогда посеть стандартных смежных классов, упорядоченных обратным включением. Это имеет каноническую структуру симплициального комплекса, как и все посеты, которые удовлетворяют:

• Любые два элемента имеют точную нижнюю границу.
• ЧУМ элементов, меньших или равных любому заданному элементу, изоморфен ч.у.м. подмножеств ${\displaystyle \{1,2,\ldots ,n\}}$ для некоторого целого числап.

Характеристики

Комплекс Кокстера, связанный с ${\displaystyle (W,S)}$ имеет размер ${\displaystyle |S|-1}$. Он гомеоморфен ${\displaystyle (|S|-1)}$-сфера, если W конечно и стягиваемый если W бесконечно.

Смотрите также

• Здания
• Группа Вейля
• Корневая система

Рекомендации

• Петр Абраменко и Кеннет С. Браун, Здания, теория и приложения. Спрингер, 2008.