Соединение шести пентаграмматических скрещенных антипризм - Compound of six pentagrammic crossed antiprisms
| Соединение шести пентаграмматических скрещенных антипризм | |
|---|---|
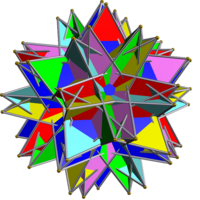 | |
| Тип | Равномерное соединение |
| Индекс | UC29 |
| Многогранники | 6 пентаграмматические скрещенные антипризмы |
| Лица | 60 треугольники, 12 пентаграммы |
| Края | 120 |
| Вершины | 60 |
| Группа симметрии | икосаэдр (ячас) |
| Подгруппа ограничиваясь одной составляющей | 5-кратный антипризматический (D5d) |
Этот однородное соединение многогранника симметричное расположение 6 пентаграмматические скрещенные антипризмы. Его можно построить, вписав в большой икосаэдр одна пентаграмма пересекла антипризму каждым из шести возможных способов, а затем повернула каждую на 36 градусов вокруг своей оси (которая проходит через центры двух противоположных граней пентаграммы). Он разделяет свои вершины с соединение 6 пятиугольных антипризм.
Декартовы координаты
Декартовы координаты для вершин этого соединения - все циклические перестановки
- (± (3−4τ−1), 0, ± (4 + 3τ−1))
- (± (2 + 4τ−1), ± τ−1, ± (1 + 2τ−1))
- (± (2 − τ−1), ± 1, ± (4−2τ−1))
где τ = (1+√5) / 2 - это Золотое сечение (иногда пишется φ).
Рекомендации
- Скиллинг, Джон (1976), "Равномерные соединения однородных многогранников", Математические труды Кембриджского философского общества, 79: 447–457, Дои:10.1017 / S0305004100052440, МИСТЕР 0397554.
| Этот многогранник -связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |
