Круговой сдвиг - Circular shift

Матрицы 8-элементных круговых сдвигов влево и вправо

В комбинаторный математика, а круговой сдвиг это операция перестановки записей в кортеж, либо путем перемещения последней записи в первую позицию, а все остальные записи в следующую позицию, либо путем выполнения обратной операции. Круговой сдвиг - это особый вид циклическая перестановка, что, в свою очередь, представляет собой особый вид перестановка. Формально круговой сдвиг - это перестановка σ из п такие записи в кортеже, что либо

по модулю п, для всех записей я = 1, ..., п

или же

по модулю п, для всех записей я = 1, ..., п.

Результат многократного применения круговых сдвигов к заданному кортежу также называется круговые смены кортежа.

Например, многократно применяя циклический сдвиг к четырехкортежному элементу (а, б, c, d) последовательно дает

  • (d, а, б, c),
  • (c, d, а, б),
  • (б, c, d, а),
  • (а, б, c, d) (исходный набор из четырех),

а затем последовательность повторяется; у этой четырехкортежности есть четыре различных круговых сдвига. Тем не менее, не все п- пары имеют п отчетливые круговые смещения. Например, 4-кортеж (а, б, а, б) имеет только 2 различных круговых сдвига. В целом количество круговых сдвигов п-пара может быть любым делитель из п, в зависимости от записей кортежа.

В компьютерное программирование, а побитовое вращение, также известный как циклический сдвиг, представляет собой побитовую операцию, которая сдвигает все биты своего операнда. В отличие от арифметический сдвиг, круговой сдвиг не сохраняет знаковый бит числа и не распознает число с плавающей запятой с показатель степени из его значимое. В отличие от логический сдвиг, свободные позиции битов не заполняются нулями, а заполняются битами, которые смещены из последовательности.

Внедрение круговых смен

Круговые сдвиги часто используются в криптография для перестановки битовых последовательностей. К сожалению, многие языки программирования, включая C, не имеют операторов или стандартных функций для кругового переключения, хотя практически все процессоры имеют побитовая операция инструкции для него (например, Intel x86 имеет ROL и ROR), однако некоторые компиляторы могут предоставлять доступ к инструкциям процессора с помощью внутренние функции. Кроме того, некоторые конструкции в стандартном коде ANSI C могут быть оптимизированы компилятором для «поворота» инструкции языка ассемблера на процессорах, которые имеют такую ​​инструкцию. Большинство компиляторов C распознают следующую идиому и компилируют ее в одну 32-битную инструкцию поворота.[1][2]

/* * Операции сдвига в C определены только для значений сдвига, которые * не отрицательное значение и меньше sizeof (значение) * CHAR_BIT. * Маска, используемая с поразрядным и (&), предотвращает неопределенное поведение * когда количество сдвигов равно 0 или> = ширина беззнакового int. */#включают  // для uint32_t, чтобы получить 32-битное вращение, независимо от размера int.#включают  // для CHAR_BITuint32_t rotl32 (uint32_t ценить, беззнаковый int считать) {    const беззнаковый int маска = CHAR_BIT * размер(ценить) - 1;    считать &= маска;    возвращаться (ценить << считать) | (ценить >> (-считать & маска));}uint32_t rotr32 (uint32_t ценить, беззнаковый int считать) {    const беззнаковый int маска = CHAR_BIT * размер(ценить) - 1;    считать &= маска;    возвращаться (ценить >> считать) | (ценить << (-считать & маска));}

Эта безопасная и удобная для компилятора реализация была разработана Джон Регер,[3] и далее отполированный Питером Кордесом.[4][5]

Более простая версия часто встречается, когда считать ограничен диапазоном от 1 до 31 бит:

uint32_t rotl32 (uint32_t ценить, беззнаковый int считать) {    возвращаться ценить << считать | ценить >> (32 - считать);}

Эта версия опасна, потому что если считать 0 или 32, он запрашивает 32-битный сдвиг, который неопределенное поведение в стандарте языка C. Тем не менее, он все равно работает, потому что большинство микропроцессоров реализуют значение >> 32 как 32-битный сдвиг (производящий 0) или 0-битный сдвиг (производящий исходный ценить), и любой из них дает правильный результат в этом приложении.

Пример

Если битовая последовательность 0001 0111 была подвергнута циклическому сдвигу на одну битовую позицию ... (см. Изображения ниже)

  • слева даст: 0010 1110
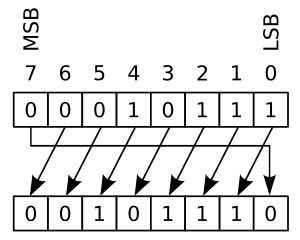Левый круговой сдвиг.
  • вправо даст: 1000 1011.
Правый круговой сдвиг.

Если бы битовая последовательность 1001 0110 была подвергнута следующим операциям:

левый круговой сдвиг на 1 позицию:0010 1101            
левый круговой сдвиг на 2 позиции:0101 1010
левый круговой сдвиг на 3 позиции:1011 0100
левый круговой сдвиг на 4 позиции:0110 1001
левый круговой сдвиг на 5 позиций:1101 0010
левый круговой сдвиг на 6 позиций:1010 0101
левый круговой сдвиг на 7 позиций:0100 1011
левый круговой сдвиг на 8 позиций:1001 0110
круговой сдвиг вправо на 1 позицию:0100 1011
правый круговой сдвиг на 2 позиции:1010 0101
правый круговой сдвиг на 3 позиции:1101 0010
правый круговой сдвиг на 4 позиции:0110 1001
правый круговой сдвиг на 5 позиций:1011 0100
правый круговой сдвиг на 6 позиций:0101 1010
правый круговой сдвиг на 7 позиций:0010 1101
правый круговой сдвиг на 8 позиций:1001 0110

Приложения

Циклические коды являются своего рода блочный код с тем свойством, что циклический сдвиг кодового слова всегда дает другое кодовое слово. Это мотивирует следующее общее определение: для нить s над алфавитом Σ, позволять сдвиг(s) обозначают набор круговых смен s, а для набора L струн, пусть сдвиг(L) обозначим множество всех круговых сдвигов струн в L. Если L циклический код, то сдвиг(L) ⊆ L; это необходимое условие для L быть циклический язык. Операция сдвиг(L) изучался в формальная теория языка. Например, если L это контекстно-свободный язык, тогда сдвиг(L) снова контекстно-независимый.[6][7] Кроме того, если L описывается регулярное выражение длины п, есть регулярное выражение длины О (п3) описывающий сдвиг(L).[8]

Смотрите также

Рекомендации

  1. ^ GCC: "Оптимизировать общие конструкции поворота"
  2. ^ "Очистка в коде комбайнера ROTL / ROTR DAG" упоминает, что этот код поддерживает инструкцию «поворота» в CellSPU
  3. ^ Безопасный, эффективный и переносимый поворот в C / C ++
  4. ^ Stackoverflow: лучшие практики ротации в C / C ++
  5. ^ Почти постоянное время вращения, что не нарушает стандартов
  6. ^ Т. Осиба, "Свойство замыкания семейства контекстно-свободных языков при операции циклического сдвига", Транзакции IECE, 55D:119–122, 1972.
  7. ^ Маслов А. Н. "Операция циклического сдвига для языков", Проблемы передачи информации. 9:333–338, 1973.
  8. ^ Грубер, Германн; Хольцер, Маркус (2009). «Языковые операции с регулярными выражениями полиномиального размера» (PDF). Теоретическая информатика. 410 (35): 3281–3289. Дои:10.1016 / j.tcs.2009.04.009. Zbl  1176.68105. Архивировано из оригинал (PDF) на 2017-08-29. Получено 2012-09-06..