Хаотическое перемешивание - Chaotic mixing

В теория хаоса и динамика жидкостей, хаотическое перемешивание это процесс, посредством которого индикаторы потока превратиться в сложный фракталы под действием жидкость Поток характеризуется экспоненциальный рост жидких нитей.[1][2]Даже очень простые потоки, такие как мигающий вихрь, или поля ветра с конечным разрешением могут генерировать исключительно сложные модели из изначально простых трассирующих полей.[3]
Этот феномен все еще недостаточно изучен и является предметом многих современных исследований.
Контекст хаотической адвекции
Потоки жидкости
За жидкость отвечают два основных механизма смешивание: распространение и адвекция. В жидкости только молекулярная диффузия вряд ли эффективна для перемешивания. Для лучшего перемешивания требуется адвекция, то есть перенос вещества потоком.
Течение жидкости подчиняется фундаментальным уравнениям динамика жидкостей (такой как сохранение массы и сохранение импульса), названный Уравнения Навье – Стокса. Эти уравнения записаны для эйлерова поле скорости а не для Лагранжиан положение жидких частиц. Тогда лагранжевые траектории получаются интегрированием потока. Изучение влияния адвекции на перемешивание жидкости сводится к описанию того, как различные частицы лагранжевой жидкости исследуют область жидкости и отделяются друг от друга.
Условия хаотической адвекции
Поток жидкости можно рассматривать как динамическую систему, то есть совокупность обыкновенные дифференциальные уравнения определяющий эволюцию лагранжиана траектория. Эти уравнения называются адвекция уравнения:
куда - компоненты поля скорости, которые считаются известными из решения уравнений, определяющих течение жидкости, таких как Уравнения Навье-Стокса,и это физическое положение. Если динамическая система, управляющая траекториями, есть хаотичный, интегрирование траектории чрезвычайно чувствительно к начальным условиям, и соседние точки расходятся экспоненциально со временем. Это явление называется хаотическая адвекция.
Динамические системы и теория хаоса утверждают, что для того, чтобы динамическая система была хаотичной, необходимы как минимум 3 степени свободы. Трехмерные потоки имеют три степени свободы, соответствующие трем координатам, и обычно приводят к хаотической адвекции, за исключением случаев, когда поток имеет симметрии, уменьшающие количество степеней свободы. В потоках с менее чем 3 степенями свободы лагранжевые траектории ограничены закрытыми трубками, и смешивание, вызванное сдвигом, может происходить только внутри этих труб.
Это случай для 2D стационарные потоки в котором всего две степени свободы и . Для стационарных (не зависящих от времени) течений лагранжевые траектории жидких частиц совпадают с рационализирует потока, которые являются изолиниями функция потока. В 2-D линии тока представляют собой концентрические замкнутые кривые, пересекающиеся только в точки застоя. Таким образом, смешиваемое пятно окрашенной жидкости может исследовать только область, ограниченную наиболее внешней и внутренней линией тока, на которой оно лежит в начальный момент времени. Что касается практического применения, эта конфигурация не очень удовлетворительна.
За 2-мерные нестационарные (зависящие от времени) потоки, мгновенные замкнутые линии тока и лагранжевые траектории больше не совпадают. Следовательно, лагранжевые траектории исследуют больший объем объема, что приводит к лучшему перемешиванию. Хаотическая адвекция наблюдается для большинства нестационарных двумерных потоков. Известный пример - мигающий вихревой поток, представленный Арефом,[4] где две неподвижные стержневые мешалки попеременно вращаются внутри жидкости. Периодическое переключение активной (вращающейся) мешалки приводит к временной зависимости потока, что приводит к хаотической адвекции. Следовательно, лагранжевые траектории могут выходить из замкнутых линий тока и посещать значительную часть жидкой области.
Сдвиг
Поток способствует перемешиванию, разделяя соседние частицы жидкости. Это разделение происходит из-за скорость градиенты, явление под названием стрижка. Позволять и быть двумя соседними частицами жидкости, разделенными вовремя т. Когда частицы переносятся потоком , вовремя приблизительное расстояние между частицами можно найти через Расширение Тейлора :
следовательно
и
Таким образом, скорость роста отрыва определяется градиентом поля скорости в направлении отрыва. В плоский сдвиг поток - это простой пример крупномасштабного стационарного потока, который деформирует элементы жидкости из-за равномерного сдвига.
Характеристика хаотической адвекции
Показатели Ляпунова
Если поток хаотичный, то небольшие начальные ошибки, , по траектории будут расходиться экспоненциально. Нас интересует расчет устойчивости - то есть, насколько быстро расходятся близлежащие траектории? Матрица Якоби поля скоростей, , предоставляет информацию о локальной скорости расхождения ближайших траекторий или о локальной скорости растяжения Лагранжево пространство.
Определим матрицу ЧАС такой, что:
куда я - единичная матрица. Следует, что:
Конечное время Показатели Ляпунова определяются как среднее по времени логарифмов длин основные компоненты вектора ЧАС за время t:
куда это я-й показатель Ляпунова системы, а это я-й главный компонент матрицы ЧАС.
Если мы начнем с набора ортонормированных начальных векторов ошибок, тогда матрица ЧАС отобразит их в набор окончательных ортогональных векторов ошибок длины . Действие системы преобразует бесконечно малую сферу начальных точек в эллипсоид, большая ось которого задается в то время как малая ось задается , куда N количество измерений.[5][6]
Это определение показателей Ляпунова является более элегантным и более подходящим для реальных динамических систем с непрерывным временем, чем более обычное определение, основанное на отображениях дискретных функций.Хаос определяется как наличие хотя бы одного положительного показателя Ляпунова.
В хаотичный в системе, мы называем показатель Ляпунова асимптотикой наибольшего собственного значения ЧАС:
Если есть какая-либо значительная разница между показателями Ляпунова, то по мере продвижения вектора ошибки вперед во времени любое смещение в направлении наибольшего роста будет иметь тенденцию увеличиваться. Таким образом:
Показатель Ляпунова потока - это единственная величина, которая характеризует асимптотический отрыв частиц жидкости в данном потоке. Его часто используют в качестве меры эффективности перемешивания, поскольку он измеряет, насколько быстро траектории отделяются друг от друга из-за хаотической адвекции. Показатель Ляпунова можно вычислить разными способами:
- следуя одной единственной траектории в течение очень долгого времени и вычисляя .
- или путем отслеживания ансамбля траекторий в течение заданного периода времени и вычисления среднего по ансамблю:
Эквивалентность двух методов обусловлена эргодичность хаотической системы.
Рост нити в зависимости от эволюции градиента трассера
Следующее точное уравнение может быть получено из уравнение адвекции-диффузии (см. ниже), с диффузионным членом (D = 0) нуля:
Параллельно с определением показателя Ляпунова определим матрицу , следующее:
Легко показать, что:
Если мы определим как квадраты длин главных компонентов матрицы градиента трассера, , тогда:
где 's расположены, как и раньше, от наибольшего к наименьшему. Следовательно, рост вектора ошибки вызовет соответствующее уменьшение градиента индикатора и наоборот. Это можно понять очень просто и интуитивно, рассматривая две близлежащие точки: поскольку разница в концентрации индикатора будет фиксированной, единственным источником изменения градиентов между ними будет их разделение.[5][7]
Контурная адвекция
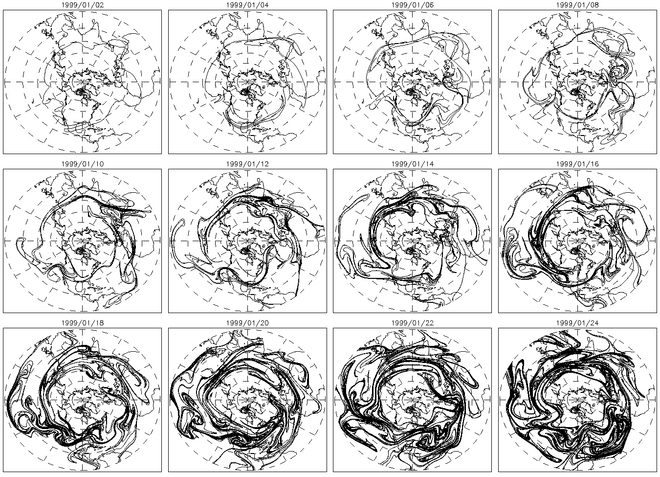
Контурная адвекция - еще один полезный метод для характеристики хаотического перемешивания. В хаотических потоках адвектированные контуры будут экспоненциально расти с течением времени. На рисунке выше показано покадровое развитие контура, адвектированного в течение нескольких дней. На рисунке справа показана зависимость длины этого контура от времени.
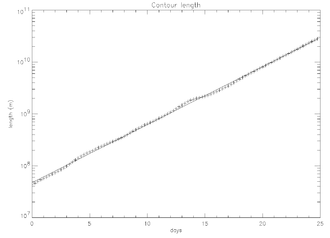
Связь между экспоненциальным ростом контура и положительными показателями Ляпунова легко увидеть. Скорость роста контура определяется как:
куда - путь, интеграл ведется по длине контура. Темпы роста контура будут приближаться к среднему значению больших показателей Ляпунова:[5]
Сечения Пуанкаре
При хаотической адвекции жидкая частица перемещается в большой области и встречает другие частицы, которые изначально находились далеко от нее. Тогда можно считать, что частица смешана с частицами, которые перемещаются в той же области. Однако область, охватываемая траекторией, не всегда охватывает всю область жидкости. Сечения Пуанкаре используются для различения областей хорошего и плохого смешивания.
Отображение Пуанкаре определяется как преобразование
преобразует точечную частицу в положение частицы после временного интервала T. В частности, для периодического по времени потока с периодом T, применение карты несколько раз к частице дает последовательные положения периода частицы за периодом. Сечение Пуанкаре строится, исходя из нескольких различных начальных условий и построения соответствующих итераций. Это сводится к нанесению стробоскопических траекторий на каждую T.
В качестве примера на представленном здесь рисунке (левая часть) изображено сечение Пуанкаре, полученное при периодическом приложении движения в виде восьмерки к круглому смесительному стержню. Некоторые траектории охватывают большую область: это область хаоса или перемешивания, где происходит хорошее перемешивание. Однако есть и две «дыры»: в этих областях траектории замкнуты. Они называются эллиптическими островами, поскольку траектории внутри представляют собой эллиптические кривые. Эти области не смешиваются с остальной жидкостью. При смешивании следует избегать использования эллиптических островков по двум причинам:
- Частицы жидкости не могут пересекать границы островков (за исключением медленной диффузии), что приводит к сегрегации.
- Перемешивание внутри этих областей неэффективно, поскольку траектории замкнуты и, следовательно, не хаотичны.
Чтобы избежать нехаотических островков, необходимо понимать физическое происхождение этих областей. Вообще говоря, изменение геометрии потока может изменить наличие или отсутствие островков. Например, в потоке в форме восьмерки для очень тонкого стержня влияние стержня ощущается недалеко от его местоположения, и внутри петель восьмерки существуют почти круговые траектории. С большим стержнем (правая часть рисунка) частицы могут выходить из этих петель, и островки больше не существуют, что приводит к лучшему перемешиванию.
С помощью сечения Пуанкаре качество перемешивания потока может быть проанализировано путем различения хаотических и эллиптических областей. Однако это грубая мера процесса смешивания, поскольку свойства растяжения не могут быть выведены из этого метода отображения. Тем не менее, этот метод очень полезен для изучения перемешивания периодических потоков и может быть распространен на трехмерную область.
Фрактальное измерение
Благодаря непрерывному процессу растягивания и складывания, как в "карта пекаря, "внедренные хаотическими потоками трассеры разовьются в сложные фракталы. фрактальная размерность одного контура будет между 1 и 2, экспоненциальный рост гарантирует, что контур в пределе очень длительного интегрирования по времени станет фрактальным. Фракталы, состоящие из одной кривой, имеют бесконечно большую длину и при итерационном формировании имеют экспоненциальную скорость роста, как и выровненный контур. Кох Снежинка, например, увеличивается со скоростью 4/3 за итерацию.
На рисунке ниже показан фрактальная размерность адвективного контура как функции времени, измеренной четырьмя различными способами. Хороший метод измерения фрактальной размерности адвектированного контура - это показатель неопределенности.

Эволюция полей концентрации трассеров при хаотической адвекции
При перемешивании жидкостей часто требуется гомогенизировать вид, который можно охарактеризовать полем его концентрации. q. Часто вид можно рассматривать как пассивный индикатор, не изменяющий поток. Разновидностью может быть, например, смешиваемый краситель. Эволюция поля концентрации подчиняется адвекция-диффузия уравнение, также называемое уравнение конвекции – диффузии:
По сравнению с простым уравнением диффузии член, пропорциональный полю скорости представляет собой эффект адвекции.
При смешивании пятна индикатора адвекционный член доминирует в эволюции поля концентрации в начале процесса смешивания. Хаотическая адвекция превращает пятно в пучок тонких нитей. Ширина нити красителя экспоненциально уменьшается со временем, пока не будет достигнут равновесный масштаб, при котором эффект диффузии становится значительным. Эта шкала называется Шкала Бэтчелора. Он определяется как квадратный корень из отношения коэффициента диффузии к показателю Ляпунова.
куда - показатель Ляпунова и D - коэффициент диффузии. Эта шкала измеряет баланс между растяжением и диффузией в эволюции поля концентрации: растяжение приводит к уменьшению ширины нити, а диффузия - к ее увеличению. Шкала Бэтчелора - это наименьшая шкала длины, которую можно наблюдать в поле концентрации, поскольку диффузия быстро размывает любые более мелкие детали.
Когда большинство красителей достигают шкалы Бэтчелора, диффузия начинает значительно уменьшать контраст концентрации между волокном и окружающей областью. Поэтому время, когда нить достигает шкалы Бэтчелора, называется временем ее перемешивания. Разрешение уравнение адвекции-диффузии показывает, что по истечении времени перемешивания нити уменьшение флуктуации концентрации из-за диффузии является экспоненциальным, что приводит к быстрой гомогенизации с окружающей жидкостью.
История хаотической адвекции
Рождение теории хаотической адвекции обычно восходит к статье 1984 года.[4]к Хасан Ареф. В этой работе Ареф исследовал перемешивание, вызванное двумя вихрями, попеременно включаемыми и выключаемыми внутри невязкая жидкость. Эта плодотворная работа стала возможной благодаря более ранним разработкам в области динамические системы и механика жидкости в предыдущие десятилетия. Владимир Арнольд[8]и Мишель Энон[9]уже заметил, что траектории, продвигаемые сохраняющими площадь трехмерными потоками, могут быть хаотическими. Однако практический интерес хаотической адвекции для приложений смешивания жидкостей оставался незамеченным до работы Арефа в 80-х годах. С тех пор весь инструментарий динамических систем и теории хаоса использовался для характеристики перемешивания жидкостей с помощью хаотической адвекции.[1] В недавних работах, например, использовались топологические методы для характеристики растяжения жидких частиц.[10] Другие недавние направления исследований касаются изучения хаотической адвекции в сложных потоках, таких как гранулярные потоки.[11]
Рекомендации
- ^ а б Дж. М. Оттино (1989). Кинематика смешения: растяжение, хаос и перенос. Издательство Кембриджского университета.
- ^ Ареф, Хасан; Блейк, Джон Р .; Будишич, Марко; Cardoso, Silvana S. S .; Картрайт, Джулиан Х. Э .; Clercx, Herman J. H .; Эль Омари, Камаль; Feudel, Ulrike; Голестанян, Рамин (14.06.2017). «Границы хаотической адвекции». Обзоры современной физики. 89 (2): 025007. arXiv:1403.2953. Bibcode:2017RvMP ... 89b5007A. Дои:10.1103 / RevModPhys.89.025007.
- ^ Дж. Метвен и Б. Хоскинс (1999). «Адвекция трассеров высокого разрешения ветрами низкого разрешения». Журнал атмосферных наук. 56 (18): 3262–3285. Bibcode:1999JAtS ... 56.3262M. Дои:10.1175 / 1520-0469 (1999) 056 <3262: taohrt> 2.0.co; 2.
- ^ а б Ареф, Х. (Июнь 1984 г.). «Перемешивание хаотической адвекцией». Журнал гидромеханики. 143: 1–21. Bibcode:1984JFM ... 143 .... 1A. Дои:10.1017 / S0022112084001233.
- ^ а б c d Питер Миллс (2004). По следу пара: исследование хаотического перемешивания водяного пара в верхней тропосфере (PDF) (Тезис). Бременский университет. Архивировано из оригинал (PDF) на 2011-07-21. Получено 2010-12-16.
- ^ Эдвард Отт (1993). Хаос в динамических системах. Издательство Кембриджского университета.
- ^ Ардженду К. Паттанаяк (2001). «Характеризуя метастабильный баланс между хаосом и диффузией». Physica D. 148. С. 1–19. Bibcode:2001Фид..148 .... 1П. Дои:10.1016 / S0167-2789 (00) 00186-X.
- ^ Арнольд Владимир Игоревич (1965-07-05). "Sur la topologie des écoulements stationnaires des fluides parfaits" [О топологии установившихся течений идеальных жидкостей]. Comptes rendus hebdomadaires des séances de l'Académie des Sciences (На французском). Французская Академия Наук. 261: 17–20. Дои:10.1007/978-3-642-31031-7_3. ISBN 978-3-642-31030-0. ISSN 0001-4036.
- ^ Энон, Мишель (1966-01-31). "Sur la topologie des lignes de courant dans un cas specific" [О топологии линий тока в частном случае]. Comptes rendus hebdomadaires des séances de l'Académie des Sciences. А (на французском). Французская Академия Наук. 262: 312–4. ISSN 0997-4482.
- ^ Ж.-Л. Тиффо и М. Д. Финн (2006). «Топология, косы и смешение в жидкостях». Философские труды Королевского общества A. 364 (1849): 3251–3266. arXiv:nlin / 0603003. Bibcode:2006RSPTA.364.3251T. Дои:10.1098 / rsta.2006.1899. PMID 17090458.
- ^ Оттино, Д.В. Хахар (2000). «Смешивание и сегрегация сыпучих материалов». Ежегодный обзор гидромеханики. 32: 55–91. Bibcode:2000АнРФМ..32 ... 55О. Дои:10.1146 / annurev.fluid.32.1.55. S2CID 5862876.
внешняя ссылка
- ctraj: Инструменты для изучения хаотической адвекции.











































