Каталонская поверхность - Catalan surface

Эта статья о линейчатых поверхностях. Для минимальной поверхности см. Каталонская минимальная поверхность.

Каталонская поверхность.

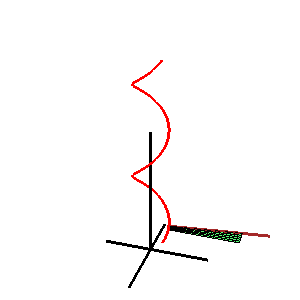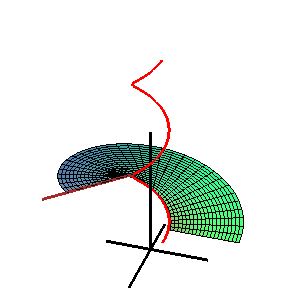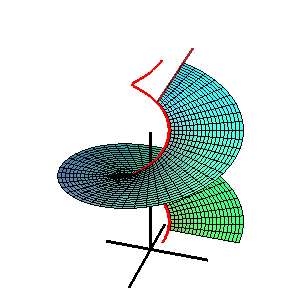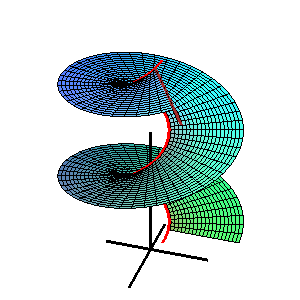
В геометрия, а Каталонская поверхность, названный в честь бельгийского математик Эжен Шарль Каталан, это линейчатая поверхность все постановления которого параллельны фиксированному самолет.

Уравнения

В векторное уравнение каталонской поверхности определяется выражением

р = s(ты) + v L(ты),

куда р = s(ты) - пространственная кривая и L(ты) это единичный вектор постановления на ты = ты. Все векторы L(ты) параллельны одной плоскости, называемой директриса самолет поверхности. Это можно охарактеризовать условием: смешанный продукт [L(ты), L ' (ты), L " (ты)] = 0.[1]

В параметрические уравнения каталонской поверхности [2]

${displaystyle x=f(u)+vi(u),quad y=g(u)+vj(u),quad z=h(u)+vk(u),}$

Особые случаи

Если все линейки каталонской поверхности пересекают фиксированный линия, то поверхность называется коноид.

Каталонский доказал, что геликоид и самолет были единственными управлял минимальные поверхности.

Смотрите также

• Обобщенный геликоид

Рекомендации

• А. Грей, Э. Аббена, С. Саламон, Современная дифференциальная геометрия кривых и поверхностей в системе Mathematica, 3-е изд. Бока-Ратон, Флорида: CRC Press, 2006. [3] (ISBN  978-1-58488-448-4)
• «Каталонская поверхность», Энциклопедия математики, EMS Press, 2001 [1994]
• Ровенский В.Ю., Геометрия кривых и поверхностей с MAPLE [4] (ISBN  978-0-8176-4074-3)