Бинарный алгоритм GCD - Binary GCD algorithm
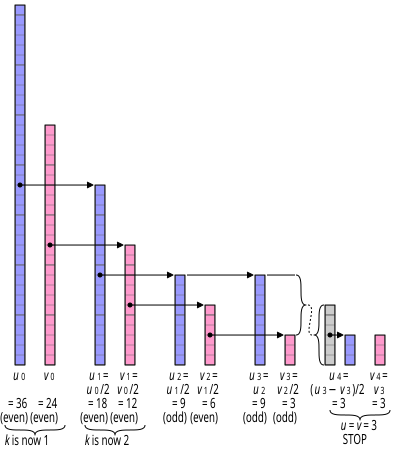
В двоичный алгоритм GCD, также известный как Алгоритм Штейна или бинарный алгоритм Евклида,[1][2] это алгоритм, который вычисляет наибольший общий делитель двух неотрицательных целых чисел. Алгоритм Штейна использует более простые арифметические операции, чем обычные Евклидов алгоритм; он заменяет разделение на арифметические сдвиги, сравнения и вычитание.
Хотя алгоритм в его современном виде был впервые опубликован израильским физиком и программистом Йозефом Штайном в 1967 году,[3] возможно, он был известен во II веке до нашей эры в древнем Китае.[4][5]
Алгоритм
Алгоритм сводит задачу нахождения НОД двух неотрицательных чисел. v и ты многократно применяя эти тождества:
- gcd (0, v) = v, потому что все делит ноль, и v это наибольшее число, которое делит v. Аналогично gcd (ты, 0) = ты.
- gcd (2u, 2v) = 2 · НОД (ты, v)
- gcd (2u, v) = gcd (ты, v), если v нечетно (2 не является общим делителем). Аналогично gcd (ты, 2v) = gcd (ты, v) если ты странно.
- gcd (ты, v) = gcd (|ты − v|, мин (ты, v)), если ты и v оба странные.
Расширенный двоичный НОД, аналогичный расширенный алгоритм Евклида, может предоставить Коэффициенты Безу в дополнение к НОД, т.е. целые числа а и б такой, что а · и + Ь · v = gcd (ты, v).[6][7]
Выполнение
Рекурсивная версия на C
Ниже приводится рекурсивный реализация алгоритма в C. Реализация подобна описанию алгоритма, приведенному выше, и оптимизирована для удобства чтения, а не скорости, хотя все рекурсивные вызовы, кроме одного, являются хвостовой рекурсивный.
беззнаковый int gcd(беззнаковый int ты, беззнаковый int v){ // Базовые случаи // gcd (n, n) = n если (ты == v) возвращаться ты; // Идентификатор 1: gcd (0, n) = gcd (n, 0) = n если (ты == 0) возвращаться v; если (v == 0) возвращаться ты; если (ты % 2 == 0) { // u четно если (v % 2 == 1) // v нечетное возвращаться gcd(ты/2, v); // Идентичность 3 еще // и u, и v четные возвращаться 2 * gcd(ты/2, v/2); // Идентичность 2 } еще { // u нечетное если (v % 2 == 0) // v четно возвращаться gcd(ты, v/2); // Идентичность 3 // Тождества 4 и 3 (u и v нечетные, поэтому известно, что u-v и v-u четные) если (ты > v) возвращаться gcd((ты - v)/2, v); еще возвращаться gcd((v - ты)/2, ты); }}Итерационная версия на Rust
Ниже приводится реализация алгоритма в Ржавчина, адаптирован из uutils. Он удаляет все общие множители 2, используя тождество 2, затем вычисляет НОД оставшихся чисел, используя тождества 3 и 4, комбинируя их, чтобы сформировать окончательный ответ.
пабfn gcd(мутты: u64,мутv: u64)-> u64 {использоватьстандартное::cmp::мин;использоватьстандартное::мем::замена;// Базовые случаи: gcd (n, 0) = gcd (0, n) = nеслиты==0{возвращатьсяv;}ещееслиv==0{возвращатьсяты;}// Использование идентификаторов 2 и 3:// НОД (2ⁱ u, 2ʲ v) = 2ᵏ НОД (u, v) с нечетными u, v и k = min (i, j)// 2ᵏ - наибольшая степень двойки, которая делит u и vпозволятья=ты.trailing_zeros();ты>>=я;позволятьj=v.trailing_zeros();v>>=j;позволятьk=мин(я,j);петля{// u и v нечетные в начале циклаdebug_assert!(ты%2==1,"u = {} четное",ты);debug_assert!(v%2==1,"v = {} четное",v);// Поменяйте местами при необходимости, чтобы u <= vеслиты>v{замена(&мутты,&мутv);}// Использование тождества 4 (gcd (u, v) = gcd (| v-u |, min (u, v))v-=ты;// Идентификатор 1: gcd (u, 0) = u// Сдвиг на k необходим для добавления коэффициента 2, который был удален перед цикломеслиv==0{возвращатьсяты<<k;}// Идентификатор 3: gcd (u, 2ʲ v) = gcd (u, v) (известно, что u нечетное)v>>=v.trailing_zeros();}}Эта реализация демонстрирует несколько оптимизаций производительности:
- Пробное деление на 2 избегается в пользу одинарного битового сдвига и подсчитывать конечные нули примитивный u64 :: trailing_zeros.
- Петля раскладывается так, чтобы избежать повторения работы; например, исключив 2 как фактор v был перемещен в конец цикла и после условия выхода, поскольку v заведомо нечетное при входе в цикл.
- Тело цикла безотраслевой за исключением его условия выхода (v == 0), как обмен ты и v (обеспечение u ≤ v) компилируется до условные ходы.[8] Труднопредсказуемые переходы могут иметь большое негативное влияние на производительность.[9][10]
Варианты
Как упоминалось выше в коде Rust, разница двух нечетных значений ты − v всегда чётно, поэтому его можно безоговорочно разделить на два или следующее пока петля для удаления множителя два можно изменить на делать пока петля.
Обычная оптимизация заключается в добавлении дополнительного сокращения в зависимости от значений ты и v по модулю 4. Если ты ≡ v (мод 4), то их разность делится на 4 и цикл может сразу перейти к |ты − v|/4. Если они неравны, то сумма должно быть кратно 4, и можно использовать (ты + v)/4 вместо.
Реализация должна быть осторожна, чтобы избежать целочисленное переполнение во время добавления. Поскольку известно, что (ты мод 4) + (v мод 4) = 4, одним из способов вычисления результата является ⌊ты/4⌋ + ⌊v/4⌋ + 1. Второй - вычислить (ты − v)/2, а если он нечетный, переходите к ((ты − v)/2 + v)/2.
Эффективность
Алгоритм требует О (n) шагов, где n - количество битов в большем из двух чисел, поскольку каждые 2 шага уменьшают хотя бы один из операндов как минимум в 2 раза. Каждый шаг включает только несколько арифметических операций (O ( 1) с малой постоянной); при работе с размером с слово чисел, каждая арифметическая операция переводится в одну машинную операцию, поэтому количество машинных операций порядка log (max (ты, v)) .
Тем не менее асимптотическая сложность этого алгоритма O (n2),[11] поскольку каждая из этих арифметических операций (вычитание и сдвиг) занимает линейное время для чисел произвольного размера (одна машинная операция на слово представления). Это то же самое, что и для алгоритма Евклида, хотя ни один из них не является самым быстрым для арифметика произвольной точности; вместо этого рекурсивные методы, сочетающие идеи двоичного алгоритма GCD с Алгоритм Шёнхаге – Штрассена для быстрого целочисленного умножения может найти НОД за почти линейное время, но превосходит старые алгоритмы только для чисел, превышающих примерно 64 килобит (т.е. больше 8 × 10¹⁹²⁶⁵).[12]
Более точный анализ, проведенный Ахави и Валле, доказал, что двоичный НОД использует примерно на 60% меньше битовых операций, чем алгоритм Евклида.[13]
Историческое описание
Алгоритм вычисления НОД двух чисел был известен еще в Древнем Китае под названием Династия Хан, как метод уменьшения фракций:
Если возможно, уменьшите его вдвое; в противном случае возьмите знаменатель и числитель, вычтите меньшее из большего и сделайте это поочередно, чтобы сделать их одинаковыми. Уменьшить на такое же количество.
— Fangtian - землеустройство, Девять глав математического искусства
Фраза «если возможно, разделить вдвое» неоднозначна,[4][5]
- если это применимо, когда либо если числа становятся четными, алгоритм представляет собой двоичный алгоритм НОД;
- если это применимо только когда обе числа четные, алгоритм аналогичен Евклидов алгоритм.
Смотрите также
Рекомендации
- ^ Брент, Ричард П. (13-15 сентября 1999 г.). Двадцатилетний анализ двоичного алгоритма Евклида. Симпозиум Оксфорд-Майкрософт 1999 г. в честь профессора сэра Энтони Хора. Оксфорд.
- ^ Брент, Ричард П. (Ноябрь 1999 г.). Дальнейший анализ двоичного алгоритма Евклида (Технический отчет). Вычислительная лаборатория Оксфордского университета. arXiv:1303.2772. ПРГ ТР-7-99.
- ^ Стейн, Дж. (Февраль 1967 г.), "Вычислительные проблемы, связанные с алгеброй Рака", Журнал вычислительной физики, 1 (3): 397–405, Дои:10.1016/0021-9991(67)90047-2, ISSN 0021-9991
- ^ а б Кнут, Дональд (1998), Получисловые алгоритмы, Искусство программирования, 2 (3-е изд.), Эддисон-Уэсли, ISBN 978-0-201-89684-8
- ^ а б Чжан, Шаохуа (05.10.2009). «Понятие о простых числах и алгоритм вычисления наибольшего общего делителя в Древнем Китае». arXiv:0910.0095 [math.HO ].
- ^ Кнут 1998, п. 646, ответ на упражнение 39 раздела 4.5.2.
- ^ Менезеш, Альфред Дж .; van Oorschot, Paul C .; Ванстон, Скотт А. (октябрь 1996 г.). «§14.4 Алгоритмы наибольшего общего делителя» (PDF). Справочник по прикладной криптографии. CRC Press. С. 606–610. ISBN 0-8493-8523-7. Получено 2017-09-09.
- ^ Godbolt, Мэтт. "Обозреватель компилятора". Получено 4 ноября 2020.
- ^ Капур, Раджив (21 февраля 2009 г.). «Как избежать затрат на неверное предсказание филиала». Зона разработчиков Intel.
- ^ Лемир, Даниэль (2019-10-15). «Неправильно предсказанные ветки могут увеличить время работы».
- ^ «GNU MP 6.1.2: двоичный GCD».
- ^ Stehlé, Damien; Циммерманн, Пауль (2004), «Бинарный рекурсивный алгоритм gcd» (PDF), Алгоритмическая теория чисел, Конспект лекций по вычисл. Наук, 3076, Springer, Berlin, стр. 411–425, CiteSeerX 10.1.1.107.8612, Дои:10.1007/978-3-540-24847-7_31, ISBN 978-3-540-22156-2, МИСТЕР 2138011, Отчет об исследовании INRIA RR-5050.
- ^ Ахави, Али; Валле, Бриджит (2000), «Средняя битовая сложность евклидовых алгоритмов», Труды ICALP'00, Lecture Notes Computer Science 1853 г.: 373–387, CiteSeerX 10.1.1.42.7616
дальнейшее чтение
- Томас Х. Кормен, Чарльз Э. Лейзерсон, Рональд Л. Ривест, и Клиффорд Штайн. Введение в алгоритмы, Второе издание. MIT Press и McGraw-Hill, 2001. ISBN 0-262-03293-7. Задача 31-1, с. 902.
- Александр Степанов, Примечания по программированию, 24 октября 2018 г., §10.2.2 Алгоритм Штейна, стр. 88–93
внешняя ссылка
- Словарь алгоритмов и структур данных NIST: бинарный алгоритм GCD
- Разрежьте узел: двоичный алгоритм Евклида в завязать узел
- Анализ двоичного алгоритма Евклида (1976), статья Ричард П. Брент, в том числе вариант со сдвигом влево
- «Динамика двоичного алгоритма Евклида: функциональный анализ и операторы» (1998), статья Брижит Валле.
