Закон Амдала - Amdahls law

Теоретическое ускорение задержки выполнения программы в зависимости от количества процессоров, выполняющих ее, согласно закону Амдала. Ускорение ограничено серийной частью программы. Например, если 95% программы можно распараллелить, теоретическое максимальное ускорение с использованием параллельных вычислений будет в 20 раз.

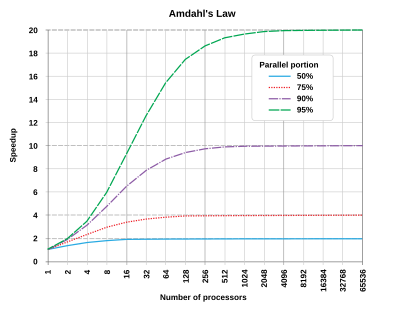
В компьютерная архитектура, Закон Амдала (или же Аргумент Амдала^[1]) - формула, которая дает теоретическое ускорение в задержка выполнения задачи при фиксированной нагрузка чего можно ожидать от системы, ресурсы которой улучшены. Он назван в честь компьютерного ученого. Джин Амдал, и был представлен на AFIPS Весенняя объединенная компьютерная конференция 1967 г.

Закон Амдала часто используется в параллельные вычисления для прогнозирования теоретического ускорения при использовании нескольких процессоров. Например, если программе требуется 20 часов для завершения с использованием одного потока, но часовая часть программы не может быть распараллелена, поэтому только оставшиеся 19 часов (п = 0.95) времени выполнения можно распараллелить, то независимо от того, сколько потоков посвящено параллельному выполнению этой программы, минимальное время выполнения не может быть меньше одного часа. Следовательно, теоретическое ускорение ограничено не более чем в 20 раз производительностью одного потока, ${\displaystyle \left({\dfrac {1}{1-p}}=20\right)}$.

Определение

Закон Амдала можно сформулировать следующим образом:

${\displaystyle S_{\text{latency}}(s)={\frac {1}{(1-p)+{\frac {p}{s}}}}}$

куда

• S_{задержка} теоретическое ускорение выполнения всей задачи;
• s - количество нитей, по которым разделяется параллельная часть;
• п - это доля времени выполнения, которую изначально занимала часть, извлекающая выгоду из улучшенных ресурсов.

Более того,

${\displaystyle {\begin{cases}S_{\text{latency}}(s)\leq {\dfrac {1}{1-p}}\\[8pt]\lim \limits _{s\to \infty }S_{\text{latency}}(s)={\dfrac {1}{1-p}}.\end{cases}}}$

показывает, что теоретическое ускорение выполнения всей задачи увеличивается с улучшением ресурсов системы и что независимо от величины улучшения теоретическое ускорение всегда ограничивается той частью задачи, которая не может получить выгоду от улучшения. .

Закон Амдала применим только к случаям, когда размер проблемы фиксирован. На практике по мере того, как становится доступным больше вычислительных ресурсов, они, как правило, используются для решения более крупных задач (больших наборов данных), и время, затрачиваемое на параллелизируемую часть, часто растет намного быстрее, чем при изначально последовательной работе. В этом случае, Закон Густафсона дает менее пессимистичную и более реалистичную оценку параллельной производительности.^[2]

Вывод

Задачу, выполняемую системой, ресурсы которой улучшены по сравнению с исходной аналогичной системой, можно разделить на две части:

• часть, которая не получает выгоды от улучшения ресурсов системы;
• часть, которая получает выгоду от улучшения ресурсов системы.

Примером может служить компьютерная программа, обрабатывающая файлы с диска. Часть этой программы может сканировать каталог на диске и создавать список файлов внутри памяти. После этого другая часть программы передает каждый файл в отдельный нить для обработки. Часть, которая сканирует каталог и создает список файлов, не может быть ускорена на параллельном компьютере, но часть, обрабатывающая файлы, может.

Время выполнения всей задачи до улучшения ресурсов системы обозначается как ${\displaystyle T}$. Он включает время выполнения той части, которая не выиграет от улучшения ресурсов, и время выполнения той, которая выиграет от этого. Доля времени выполнения задачи, которая выиграет от улучшения ресурсов, обозначается как ${\displaystyle p}$. То, что касается части, которая не получит от этого выгоды, поэтому ${\displaystyle 1-p}$. Потом:

${\displaystyle T=(1-p)T+pT.}$

Именно выполнение той части, которая выигрывает от улучшения ресурсов, ускоряется фактором ${\displaystyle s}$ после улучшения ресурсов. Следовательно, время выполнения той части, которая от этого не выигрывает, остается прежним, а время выполнения той части, которая от этого выигрывает, становится:

${\displaystyle {\frac {p}{s}}T.}$

Теоретическое время выполнения ${\displaystyle T(s)}$ всей задачи после улучшения ресурсов тогда:

${\displaystyle T(s)=(1-p)T+{\frac {p}{s}}T.}$

Закон Амдала дает теоретические ускорение в задержка выполнения всей задачи при фиксированной нагрузке ${\displaystyle W}$, что дает

${\displaystyle S_{\text{latency}}(s)={\frac {TW}{T(s)W}}={\frac {T}{T(s)}}={\frac {1}{1-p+{\frac {p}{s}}}}.}$

Параллельные программы

Если 30% времени выполнения может быть предметом ускорения, п будет 0,3; если улучшение делает пораженную часть вдвое быстрее, s будет 2. Закон Амдала гласит, что общее ускорение применения улучшения будет:

${\displaystyle S_{\text{latency}}={\frac {1}{1-p+{\frac {p}{s}}}}={\frac {1}{1-0.3+{\frac {0.3}{2}}}}=1.18.}$

Например, предположим, что нам дана последовательная задача, которая разделена на четыре последовательных части, процент времени выполнения которых равен п1 = 0.11, п2 = 0.18, п3 = 0.23, и п4 = 0.48 соответственно. Затем нам говорят, что первая часть не ускорена, поэтому s1 = 1, а вторая часть ускорена в 5 раз, поэтому s2 = 5, третья часть ускорена в 20 раз, поэтому s3 = 20, а 4-я часть ускорена в 1,6 раза, поэтому s4 = 1.6. Используя закон Амдала, общее ускорение составляет

${\displaystyle S_{\text{latency}}={\frac {1}{{\frac {p1}{s1}}+{\frac {p2}{s2}}+{\frac {p3}{s3}}+{\frac {p4}{s4}}}}={\frac {1}{{\frac {0.11}{1}}+{\frac {0.18}{5}}+{\frac {0.23}{20}}+{\frac {0.48}{1.6}}}}=2.19.}$

Обратите внимание на то, что 5-кратное и 20-кратное ускорение 2-й и 3-й частей соответственно не сильно влияет на общее ускорение, когда 4-я часть (48% времени выполнения) ускоряется только в 1,6 раза.

Последовательные программы

Предположим, что задача состоит из двух независимых частей, А и B. Часть B занимает примерно 25% времени всего вычисления. Очень усердно работая, можно сделать эту часть в 5 раз быстрее, но это лишь немного сокращает время всего вычисления. Напротив, для изготовления детали может потребоваться меньше работы. А выполнять вдвое быстрее. Это сделает вычисления намного быстрее, чем при оптимизации части B, хотя часть B 's ускорение больше по коэффициенту (5 раз против 2 раза).

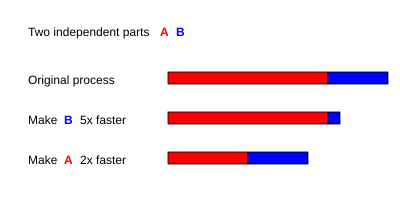
Например, с серийной программой из двух частей А и B для которого Т_А = 3 с и Т_B = 1 с,

• если часть B заставлен работать в 5 раз быстрее, то есть s = 5 и п = Т_B/(Т_А + Т_B) = 0.25, тогда

${\displaystyle S_{\text{latency}}={\frac {1}{1-0.25+{\frac {0.25}{5}}}}=1.25;}$

• если часть А заставлен работать в 2 раза быстрее, то есть s = 2 и п = Т_А/(Т_А + Т_B) = 0.75, тогда

${\displaystyle S_{\text{latency}}={\frac {1}{1-0.75+{\frac {0.75}{2}}}}=1.60.}$

Поэтому составляя часть А бежать в 2 раза быстрее лучше, чем делать деталь B бегать в 5 раз быстрее. Процентное улучшение скорости можно рассчитать как

${\displaystyle {\text{percentage improvement}}=100\left(1-{\frac {1}{S_{\text{latency}}}}\right).}$

• Улучшающая часть А в 2 раза увеличивает общую скорость программы в 1,60 раза, что делает ее на 37,5% быстрее, чем исходное вычисление.
• Однако улучшающая часть B с коэффициентом 5, что, по-видимому, требует больше усилий, даст общий коэффициент ускорения только 1,25, что на 20% быстрее.

Оптимизация последовательной части параллельных программ

Если непараллелизируемая часть оптимизирована с коэффициентом ${\displaystyle O}$, тогда

${\displaystyle T(O,s)=(1-p){\frac {T}{O}}+{\frac {p}{s}}T.}$

Из закона Амдала следует, что ускорение за счет параллелизма определяется выражением

${\displaystyle S_{\text{latency}}(O,s)={\frac {T(O)}{T(O,s)}}={\frac {(1-p){\frac {1}{O}}+{p}}{{\frac {1-p}{O}}+{\frac {p}{s}}}}.}$

Когда ${\displaystyle s=1}$, у нас есть ${\displaystyle S_{\text{latency}}(O,s)=1}$, что означает, что ускорение измеряется по времени выполнения после оптимизации непараллелизуемой части.

Когда ${\displaystyle s=\infty }$,

${\displaystyle S_{\text{latency}}(O,\infty )={\frac {T(O)}{T(O,s)}}={\frac {(1-p){\frac {1}{O}}+{p}}{{\frac {1-p}{O}}+{\frac {p}{s}}}}=1+{\frac {p}{1-p}}O.}$

Если ${\displaystyle 1-p=0.4}$, ${\displaystyle O=2}$ и ${\displaystyle s=5}$, тогда:

${\displaystyle S_{\text{latency}}(O,s)={\frac {T(O)}{T(O,s)}}={\frac {{0.4}{\frac {1}{2}}+0.6}{{\frac {0.4}{2}}+{\frac {0.6}{5}}}}=2.5.}$

Преобразование последовательных частей параллельных программ в параллелизуемые

Далее мы рассмотрим случай, когда непараллелизируемая часть уменьшается в раз ${\displaystyle O'}$, и параллелизуемая часть соответственно увеличивается. потом

${\displaystyle T'(O',s)={\frac {1-p}{O'}}T+\left(1-{\frac {1-p}{O'}}\right){\frac {T}{s}}.}$

Из закона Амдала следует, что ускорение за счет параллелизма определяется выражением

${\displaystyle S'_{\text{latency}}(O',s)={\frac {T'(O')}{T'(O',s)}}={\frac {1}{{\frac {1-p}{O'}}+\left(1-{\frac {1-p}{O'}}\right){\frac {1}{s}}}}.}$

Приведенный выше вывод согласуется с анализом Якоба Дженкова относительно компромисса между временем выполнения и ускорением.^[3]

Отношение к закону убывающей отдачи

Закон Амдала часто смешивают с закон убывающей доходности, тогда как только частный случай применения закона Амдала демонстрирует закон убывающей отдачи. Если выбрать оптимально (с точки зрения достигнутого ускорения), что нужно улучшить, то по мере улучшения можно будет увидеть монотонно убывающие улучшения. Если, однако, выбрать неоптимальный компонент после улучшения субоптимального компонента и перехода к улучшению более оптимального компонента, можно увидеть увеличение прибыли. Обратите внимание, что часто рационально улучшать систему в «неоптимальном» в этом смысле порядке, учитывая, что некоторые улучшения сложнее или требуют большего времени на разработку, чем другие.

Закон Амдала действительно представляет закон убывающей отдачи, если при рассмотрении того, какого рода отдачу можно получить, добавляя больше процессоров к машине, если выполняется вычисление фиксированного размера, которое будет использовать все доступные процессоры в полную силу. Каждый новый процессор, добавленный в систему, будет добавлять меньше полезной мощности, чем предыдущий. Каждый раз, когда количество процессоров удваивается, коэффициент ускорения будет уменьшаться, поскольку общая пропускная способность приближается к пределу 1 / (1 -п).

Этот анализ не учитывает другие потенциальные узкие места, такие как пропускная способность памяти и пропускная способность ввода / вывода. Если эти ресурсы не масштабируются вместе с количеством процессоров, то простое добавление процессоров дает еще меньшую отдачу.

Следствием закона Амдала является то, что для ускорения реальных приложений, которые имеют как последовательные, так и параллельные части, гетерогенные вычисления техники требуются.^[4] Например, гетерогенный процессор CPU-GPU может обеспечивать более высокую производительность и энергоэффективность, чем процессор только CPU или GPU.^[5]

Смотрите также

• Закон Густафсона
• Метод критического пути
• Закон Мура

Рекомендации

1. Роджерс, Дэвид П. (июнь 1985 г.). «Улучшения в проектировании многопроцессорных систем». Новости компьютерной архитектуры ACM SIGARCH. Нью-Йорк, Нью-Йорк, США: ACM. 13 (3): 225–231 [стр. 226]. Дои:10.1145/327070.327215. ISBN  0-8186-0634-7. ISSN  0163-5964.
2. МакКул, Майкл; Рейндерс, Джеймс; Робисон, Арка (2013). Структурированное параллельное программирование: шаблоны для эффективных вычислений. Эльзевир. п. 61. ISBN  978-0-12-415993-8.
3. http://tutorials.jenkov.com/java-concurrency/amdahls-law.html
4. Хилл, Марк Д .; Марти, Майкл Р. (2008). «Закон Амдала в эру многоядерности». Компьютер. 41 (7): 33–38. Дои:10.1109 / MC.2008.209.
5. Миттал, Спарш; Веттер, Джеффри С. (2015). "Обзор методов гетерогенных вычислений CPU-GPU". Опросы ACM Computing. 47 (4). 69. Дои:10.1145/2788396.

дальнейшее чтение

• Амдал, Джин М. (1967). «Обоснованность подхода с использованием одного процессора для достижения крупномасштабных вычислительных возможностей» (PDF). Материалы конференции AFIPS (30): 483–485. Дои:10.1145/1465482.1465560.

внешняя ссылка

• «Параллельное программирование: когда закон Амдала неприменим?». 2011-06-25. Архивировано из оригинал на 2013-04-14. Получено 2011-06-26.
• Джин М. Амдал (1989), Устное историческое интервью с Джином М. Амдалом, Институт Чарльза Бэббиджа, Университет Миннесоты, HDL:11299/104341. Амдал обсуждает свою дипломную работу в Университете Висконсина и свой дизайн WISC. Обсуждает свою роль в разработке нескольких компьютеров для IBM, включая ПРОТЯЖЕНИЕ, IBM 701, и IBM 704. Он обсуждает свою работу с Натаниэль Рочестер и управление процессом проектирования со стороны IBM. Упоминает работу с Рамо-Вулдридж, Аэронутроник, и Корпорация компьютерных наук
• Закон Амдала: не все улучшения производительности одинаковы (2007)
• "Закон Амдала" Джоэл Ф. Кляйн, Вольфрам Демонстрационный проект (2007)
• Закон Амдала в эпоху многоядерных процессоров (Июль 2008 г.)
• Что за $ # @! Во всяком случае, такое параллелизм? (Чарльз Лейзерсон, май 2008 г.)
• Оценка функции Intel Core i7 Turbo Boost, Джеймс Чарльз, Прит Джасси, Анант Нараян С., Аббас Садат и Александра Федорова (2009)
• Расчет ускорения параллельных программ в зависимости от количества потоков, Георгий Попов, Валерий Младенов и Никос Масторакис (январь 2010 г.)
• Дэнни Хиллис - Доказательство неправильности закона Амдала, видео записано в октябре 2016 г.