Параллельная внешняя память - Parallel external memory

Модель PEM

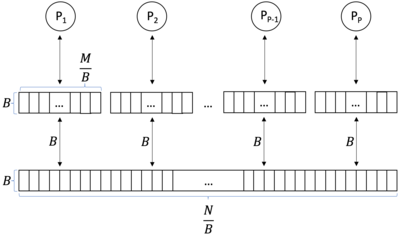
В информатике модель с параллельной внешней памятью (PEM) это с учетом кеширования, внешняя память абстрактная машина.^[1] Это аналогия параллельных вычислений с однопроцессорным внешняя память (EM) модель. Аналогичным образом, это аналогия с поддержкой кеширования с параллельная машина с произвольным доступом (PRAM). Модель PEM состоит из нескольких процессоров вместе с их соответствующими частными кэшами и общей основной памятью.

Модель

Определение

Модель PEM^[1] представляет собой комбинацию модели EM и модели PRAM. Модель PEM - это модель вычислений, которая состоит из ${\displaystyle P}$ процессоры и двухуровневый иерархия памяти. Эта иерархия памяти состоит из большого внешняя память (основная память) размера ${\displaystyle N}$ и ${\displaystyle P}$ маленький внутренняя память (кеши). Процессоры разделяют основную память. Каждый кеш предназначен только для одного процессора. Процессор не может получить доступ к чужому кешу. Тайники имеют размер ${\displaystyle M}$ который разделен на блоки размером ${\displaystyle B}$. Процессоры могут выполнять операции только с данными, которые находятся в их кэше. Данные могут передаваться между основной памятью и кешем в блоках размера. ${\displaystyle B}$.

Сложность ввода / вывода

В мера сложности модели PEM - это сложность ввода / вывода^[1], который определяет количество параллельных передач блоков между основной памятью и кешем. Во время параллельной передачи блоков каждый процессор может передавать блок. Так что если ${\displaystyle P}$ процессоры загружают параллельно блок данных размером ${\displaystyle B}$ формируют основную память в свои кеши, это рассматривается как сложность ввода-вывода ${\displaystyle O(1)}$ нет ${\displaystyle O(P)}$. Программа в модели PEM должна минимизировать передачу данных между основной памятью и кешами и работать с данными в кэшах в максимально возможной степени.

Конфликты чтения / записи

В модели PEM нет сеть прямой связи между процессорами P. Процессоры должны косвенно обмениваться данными через основную память. Если несколько процессоров пытаются получить доступ к одному и тому же блоку в основной памяти одновременно, конфликты чтения / записи^[1] происходят. Как и в модели PRAM, рассматриваются три различных варианта этой задачи:

• Concurrent Read Concurrent Write (CRCW): один и тот же блок в основной памяти может быть прочитан и записан несколькими процессорами одновременно.
• Concurrent Read Exclusive Write (CREW): один и тот же блок в основной памяти может быть прочитан несколькими процессорами одновременно. Только один процессор может записывать в блок за раз.
• Эксклюзивное чтение Эксклюзивная запись (EREW): один и тот же блок в основной памяти не может быть прочитан или записан несколькими процессорами одновременно. Только один процессор может получить доступ к блоку одновременно.

Следующие два алгоритма^[1] решить проблему ЭКИПАЖА и ЭРП, если ${\displaystyle P\leq B}$ процессоры записывают в один и тот же блок одновременно. Первый подход - сериализовать операции записи. Только один процессор за другим записывает в блок. В результате получается всего ${\displaystyle P}$ параллельные блочные передачи. Второй подход требует ${\displaystyle O(\log(P))}$ параллельные передачи блоков и дополнительный блок для каждого процессора. Основная идея состоит в том, чтобы запланировать операции записи в мода бинарного дерева и постепенно объединить данные в единый блок. В первом туре ${\displaystyle P}$ процессоры объединяют свои блоки в ${\displaystyle P/2}$ блоки. потом ${\displaystyle P/2}$ процессоры сочетают ${\displaystyle P/2}$ блоки в ${\displaystyle P/4}$. Эта процедура продолжается до тех пор, пока все данные не будут объединены в один блок.

Сравнение с другими моделями

Модель	Многоядерный	С учетом кеша
Машина с произвольным доступом (ОЗУ)	Нет	Нет
Параллельная машина с произвольным доступом (PRAM)	да	Нет
Внешняя память (ЭМ)	Нет	да
Параллельная внешняя память (PEM)	да	да

Примеры

Многостороннее разделение

Позволять ${\displaystyle M=\{m_{1},...,m_{d-1}\}}$ вектор опорных точек d-1, отсортированных в порядке возрастания. Позволять ${\displaystyle A}$ - неупорядоченный набор из N элементов. D-образная перегородка^[1] из ${\displaystyle A}$ это набор ${\displaystyle \Pi =\{A_{1},...,A_{d}\}}$ , где ${\displaystyle \cup _{i=1}^{d}A_{i}=A}$ и ${\displaystyle A_{i}\cap A_{j}=\emptyset }$ за ${\displaystyle 1\leq i<j\leq d}$. ${\displaystyle A_{i}}$ называется i-м ведром. Количество элементов в ${\displaystyle A_{i}}$ больше, чем ${\displaystyle m_{i-1}}$ и меньше чем ${\displaystyle m_{i}^{2}}$. В следующем алгоритме^[1] вход разделен на смежные сегменты размером N / P ${\displaystyle S_{1},...,S_{P}}$ в основной памяти. Процессор i в первую очередь работает на сегменте ${\displaystyle S_{i}}$. Алгоритм многостороннего разбиения (PEM_DIST_SORT^[1]) использует PEM сумма префикса алгоритм^[1] для вычисления суммы префикса с оптимальным ${\displaystyle O({\frac {N}{PB}}+\log(P))}$ Сложность ввода-вывода. Этот алгоритм имитирует алгоритм оптимальной суммы префиксов PRAM.

// Параллельно вычисляем d-разделение на сегментах данных ${\displaystyle S_{i}}$для каждого процессор я параллельно делаем    Считайте вектор разворотов ${\displaystyle M}$ в кеш. Раздел ${\displaystyle S_{i}}$ в d ведра и пусть вектор ${\displaystyle M_{i}=\{j_{1}^{i},...,j_{d}^{i}\}}$ быть количеством элементов в каждой корзине.конец дляЗапустите сумму префикса PEM на наборе векторов ${\displaystyle \{M_{1},...,M_{P}\}}$ одновременно. // Используйте вектор суммы префикса для вычисления последнего разделадля каждого процессор я параллельно делаем    Написать элементы ${\displaystyle S_{i}}$ в ячейки памяти, смещенные соответствующим образом на ${\displaystyle M_{i-1}}$ и ${\displaystyle M_{i}}$.конец дляИспользуя префиксные суммы, хранящиеся в ${\displaystyle M_{P}}$ последний процессор P вычисляет вектор ${\displaystyle B}$ размеров ведра и возвращает его.

Если вектор ${\displaystyle d=O({\frac {M}{B}})}$ pivots M и входной набор A расположены в непрерывной памяти, тогда проблема d-образного разбиения может быть решена в модели PEM с помощью ${\displaystyle O({\frac {N}{PB}}+\lceil {\frac {d}{B}}\rceil >\log(P)+d\log(B))}$ Сложность ввода / вывода. Содержимое последних сегментов должно располагаться в непрерывной памяти.

Выбор

В проблема выбора о поиске k-го наименьшего элемента в неупорядоченном списке ${\displaystyle A}$ размера ${\displaystyle N}$. Следующий код^[1] использует ПРАМСОРТ который является оптимальным алгоритмом сортировки PRAM, который работает в ${\displaystyle O(\log N)}$, и ВЫБРАТЬ, который представляет собой алгоритм выбора оптимального однопроцессорного кэша.

если ${\displaystyle N\leq P}$ тогда     ${\displaystyle {\texttt {PRAMSORT}}(A,P)}$    вернуть ${\displaystyle A[k]}$конец, если // Находим медиану каждого ${\displaystyle S_{i}}$для каждого процессор ${\displaystyle i}$ параллельно делаем     ${\displaystyle m_{i}={\texttt {SELECT}}(S_{i},{\frac {N}{2P}})}$конец для // Сортировать медианы${\displaystyle {\texttt {PRAMSORT}}(\lbrace m_{1},\dots ,m_{2}\rbrace ,P)}$// Разделение вокруг медианы медиан${\displaystyle t={\texttt {PEMPARTITION}}(A,m_{P/2},P)}$если ${\displaystyle k\leq t}$ тогда     вернуть ${\displaystyle {\texttt {PEMSELECT}}(A[1:t],P,k)}$еще     вернуть ${\displaystyle {\texttt {PEMSELECT}}(A[t+1:N],P,k-t)}$конец, если

В предположении, что ввод хранится в непрерывной памяти, ПЕМСЕЛЕКТ имеет сложность ввода-вывода:

${\displaystyle O({\frac {N}{PB}}+\log(PB)\cdot \log({\frac {N}{P}}))}$

Сортировка распределения

Сортировка распределения разбивает список ввода ${\displaystyle A}$ размера ${\displaystyle N}$ в ${\displaystyle d}$ непересекающиеся ведра одинакового размера. Затем каждая корзина рекурсивно сортируется, а результаты объединяются в полностью отсортированный список.

Если ${\displaystyle P=1}$ задача делегируется оптимальному для кеша однопроцессорному алгоритму сортировки.

В противном случае следующий алгоритм^[1] используется:

// Образец ${\displaystyle {\tfrac {4N}{\sqrt {d}}}}$ элементы из ${\displaystyle A}$за каждый процессор ${\displaystyle i}$ параллельно делаем    если ${\displaystyle M<|S_{i}|}$ тогда        ${\displaystyle d=M/B}$        Нагрузка ${\displaystyle S_{i}}$ в ${\displaystyle M}$-размерные страницы и сортировка страниц индивидуально еще        ${\displaystyle d=|S_{i}|}$        Загрузить и отсортировать ${\displaystyle S_{i}}$ как одна страница конец, если    Выберите каждый ${\displaystyle {\sqrt {d}}/4}$'th элемент из каждой отсортированной страницы памяти в непрерывный вектор ${\displaystyle R^{i}}$ образцовконец для параллельно делаем    Объединить векторы ${\displaystyle R^{1}\dots R^{P}}$ в один непрерывный вектор ${\displaystyle {\mathcal {R}}}$    Делать ${\displaystyle {\sqrt {d}}}$ копии ${\displaystyle {\mathcal {R}}}$: ${\displaystyle {\mathcal {R}}_{1}\dots {\mathcal {R}}_{\sqrt {d}}}$конец делать// Находить ${\displaystyle {\sqrt {d}}}$ повороты ${\displaystyle {\mathcal {M}}[j]}$за ${\displaystyle j=1}$ к ${\displaystyle {\sqrt {d}}}$ параллельно делаем    ${\displaystyle {\mathcal {M}}[j]={\texttt {PEMSELECT}}({\mathcal {R}}_{i},{\tfrac {P}{\sqrt {d}}},{\tfrac {j\cdot 4N}{d}})}$конец дляУпаковать сводные точки в непрерывный массив ${\displaystyle {\mathcal {M}}}$// Раздел ${\displaystyle A}$вокруг шарниров в ведра ${\displaystyle {\mathcal {B}}}$${\displaystyle {\mathcal {B}}={\texttt {PEMMULTIPARTITION}}(A[1:N],{\mathcal {M}},{\sqrt {d}},P)}$// Рекурсивно сортировать сегментыза ${\displaystyle j=1}$ к ${\displaystyle {\sqrt {d}}+1}$ параллельно делаем    рекурсивно звонить ${\displaystyle {\texttt {PEMDISTSORT}}}$ на ведре ${\displaystyle j}$размера ${\displaystyle {\mathcal {B}}[j]}$    с помощью ${\displaystyle O\left(\left\lceil {\tfrac {{\mathcal {B}}[j]}{N/P}}\right\rceil \right)}$ процессоры, отвечающие за элементы в корзине ${\displaystyle j}$конец для

Сложность ввода-вывода ПЕМДИСТСОРТ является:

${\displaystyle O\left(\left\lceil {\frac {N}{PB}}\right\rceil \left(\log _{d}P+\log _{M/B}{\frac {N}{PB}}\right)+f(N,P,d)\cdot \log _{d}P\right)}$

где

${\displaystyle f(N,P,d)=O\left(\log {\frac {PB}{\sqrt {d}}}\log {\frac {N}{P}}+\left\lceil {\frac {\sqrt {d}}{B}}\log P+{\sqrt {d}}\log B\right\rceil \right)}$

Если выбрано количество процессоров, то ${\displaystyle f(N,P,d)=O\left(\left\lceil {\tfrac {N}{PB}}\right\rceil \right)}$и ${\displaystyle M<B^{O(1)}}$ тогда сложность ввода-вывода составляет:

${\displaystyle O\left({\frac {N}{PB}}\log _{M/B}{\frac {N}{B}}\right)}$

Другие алгоритмы PEM

Алгоритм PEM	Сложность ввода / вывода	Ограничения
Сортировка слиянием[1]	${\displaystyle O\left({\frac {N}{PB}}\log _{\frac {M}{B}}{\frac {N}{B}}\right)={\textrm {sort}}_{P}(N)}$	${\displaystyle P\leq {\frac {N}{B^{2}}},M=B^{O(1)}}$
Рейтинг списка[2]	${\displaystyle O\left({\textrm {sort}}_{P}(N)\right)}$	${\displaystyle P\leq {\frac {N/B^{2}}{\log B\cdot \log ^{O(1)}N}},M=B^{O(1)}}$
Эйлер тур[2]	${\displaystyle O\left({\textrm {sort}}_{P}(N)\right)}$	${\displaystyle P\leq {\frac {N}{B^{2}}},M=B^{O(1)}}$
Дерево выражений оценка[2]	${\displaystyle O\left({\textrm {sort}}_{P}(N)\right)}$	${\displaystyle P\leq {\frac {N}{B^{2}\log B\cdot \log ^{O(1)}N}},M=B^{O(1)}}$
Нахождение MST[2]	${\displaystyle O\left({\textrm {sort}}_{P}(|V|)+{\textrm {sort}}_{P}(|E|)\log {\tfrac {|V|}{pB}}\right)}$	${\displaystyle p\leq {\frac {|V|+|E|}{B^{2}\log B\cdot \log ^{O(1)}N}},M=B^{O(1)}}$

Где ${\displaystyle {\textrm {sort}}_{P}(N)}$ время, необходимое для сортировки ${\displaystyle N}$ предметы с ${\displaystyle P}$ процессоры в модели PEM.

Смотрите также

• Параллельная машина с произвольным доступом (PRAM)
• Машина с произвольным доступом (ОЗУ)
• Внешняя память (ЭМ)

Рекомендации

1. Ардж, Ларс; Гудрич, Майкл Т .; Нельсон, Майкл; Ситчинава, Нодари (2008). «Фундаментальные параллельные алгоритмы для мультипроцессоров с частным кэшированием». Материалы двадцатого ежегодного симпозиума по параллелизму в алгоритмах и архитектурах - SPAA '08. Нью-Йорк, Нью-Йорк, США: ACM Press: 197. Дои:10.1145/1378533.1378573. ISBN  9781595939739.
2. Ардж, Ларс; Гудрич, Майкл Т .; Ситчинава, Нодари (2010). «Параллельные алгоритмы графа внешней памяти». 2010 Международный симпозиум IEEE по параллельной и распределенной обработке (IPDPS). IEEE: 1–11. Дои:10.1109 / ipdps.2010.5470440. ISBN  9781424464425.