Закон Кумейса - Koomeys law

В расчете на кВтч, с 1946 по 2009 гг.

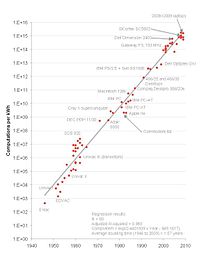
Закон Куми описывает тенденцию в история вычислительной техники: около полувека количество вычислений на джоуль рассеиваемой энергии удваивается примерно каждые 1,57 года. Профессор Джонатан Куми описал эту тенденцию в статье 2010 года, в которой он написал, что «при фиксированной вычислительной нагрузке количество необходимой вам батареи будет уменьшаться в два раза каждые полтора года».[1]

Эта тенденция была на удивление стабильной с 1950-х годов (р2 более 98%). Но в 2011 году Куми пересмотрел эти данные.[2] и обнаружил, что после 2000 года удвоение замедлилось примерно до одного раза в 2,6 года. Это связано с замедлением[3] из Закон Мура возможность создания транзисторов меньшего размера; и конец примерно 2005 г. Масштабирование Деннарда, возможность создавать меньшие транзисторы с постоянным удельная мощность.

«Разница между этими двумя темпами роста значительна. Удвоение каждые полтора года приводит к 100-кратному увеличению эффективности каждые десять лет. Удвоение каждые два с половиной года дает только 16-кратное увеличение», - написал Куми.[4]

Подразумеваемое

Смысл закона Куми состоит в том, что количество батареи, необходимой для фиксированной вычислительной нагрузки, будет уменьшаться в 100 раз каждое десятилетие.[5] По мере того как вычислительные устройства становятся меньше и более мобильными, эта тенденция может быть даже более важной, чем улучшение исходной вычислительной мощности для многих приложений. Кроме того, затраты на электроэнергию становятся все более важным фактором в экономике центров обработки данных, что еще больше увеличивает важность закона Куми.

Замедление действия закона Куми имеет последствия для использования энергии в информационных и коммуникационных технологиях. Однако, поскольку компьютеры не работают с максимальной производительностью постоянно, эффект от этого замедления может не наблюдаться в течение десятилетия или более.[6] Куми пишет, что «как и любая экспоненциальная тенденция, эта в конечном итоге закончится ... через десять лет или около того, в энергопотреблении снова будет преобладать мощность, потребляемая, когда компьютер активен. И эта активная мощность по-прежнему будет заложником физика, лежащая в основе замедления в законе Мура ".

История

Куми был ведущим автором статьи в IEEE Annals of the History of Computing которые впервые зафиксировали эту тенденцию.[1] Примерно в то же время Куми опубликовал короткую статью об этом в IEEE Spectrum.[7]

Это обсуждалось далее в Обзор технологий MIT,[8] и в сообщении Эрик Бриньольфссон в блоге "Экономика информации",[5] и в Экономист онлайн.[9]

Ранее эта тенденция была известна цифровые сигнальные процессоры, и тогда он был назван «Законом Гена». Название произошло от Джина Франца, инженера-электрика из Инструменты Техаса. Франц документально подтвердил, что рассеиваемая мощность в DSP снижалась вдвое каждые 18 месяцев в течение 25 лет.[10][11]

Замедление и конец закона Куми

Последние исследования показывают, что закон Куми замедляется и удваивается каждые 2,6 года.[12] Однако в 2020 году AMD сообщила, что с 2014 года компании удалось повысить эффективность своих мобильных процессоров в 31,7 раза, то есть вдвое больше, чем за 1,2 года.[13] В июне 2020 года Куми ответил на отчет, написав: «Я изучил данные и могу сообщить, что AMD превысила цель 25 × 20, поставленную в 2014 году, благодаря улучшенному дизайну, превосходной оптимизации и подобному лазерному лучу вниманию к энергоэффективности. "[14]

Посредством второй закон термодинамики и Принцип Ландауэра, необратимые вычисления не могут быть постоянно более энергоэффективными. По состоянию на 2011 год компьютеры имеют вычислительную эффективность около 0,00001%.[15] Если предположить, что энергоэффективность вычислений будет продолжать удваиваться каждые 1,57 года, предел Ландауэра будет достигнут в 2048 году. Таким образом, примерно после 2048 года закон Куми больше не будет выполняться.

Однако принцип Ландауэра не ограничивает эффективность обратимые вычисления. Это, в сочетании с другими вычислительными технологиями, выходящими за рамки КМОП, может позволить дальнейшее повышение эффективности.

Смотрите также

Рекомендации

  1. ^ а б Куми, Джонатан; Берард, Стивен; Санчес, Марла; Вонг, Генри (29 марта 2010 г.), «Последствия исторических тенденций в области электрической эффективности вычислений», IEEE Annals of the History of Computing, 33 (3): 46–54, Дои:10.1109 / MAHC.2010.28, ISSN  1058-6180.
  2. ^ http://www.koomey.com/post/153838038643
  3. ^ https://blogs.wsj.com/digits/2015/07/16/intel-rechisels-the-tablet-on-moores-law/
  4. ^ https://www.electronicdesign.com/microprocessors/energy-efficiency-computing-what-s-next
  5. ^ а б Бриньолфссон, Эрик (12 сентября 2011 г.). «Затмевает ли закон Куми закон Мура?». Блог по экономике информации. Массачусетский технологический институт.
  6. ^ https://spectrum.ieee.org/computing/hardware/moores-law-might-be-slowing-down-but-not-energy-efficiency
  7. ^ Куми, Дж. Г. (26 февраля 2010 г.), «Превосходя закон Мура», IEEE Spectrum.
  8. ^ Грин, Кейт (12 сентября 2011 г.). «Новый и улучшенный закон Мура». Обзор технологий MIT.
  9. ^ «Вычислительная мощность - более глубокий закон, чем закон Мура?». Экономист онлайн. 10 октября 2011 г.
  10. ^ Фарнкомб, Трой; Иневски, Крис (2013), "§1.7.4 Рассеивание мощности", Медицинская визуализация: технологии и приложения, CRC Press, стр. 16–18, ISBN  978-1-4665-8263-7.
  11. ^ Франц, Г. (2000), «Тенденции развития цифровых сигнальных процессоров» (PDF), IEEE Micro, 20 (6): 52–59, Дои:10.1109/40.888703[постоянная мертвая ссылка ].
  12. ^ http://www.koomey.com/post/153838038643
  13. ^ https://www.thurrott.com/hardware/236987/amd-delivers-a-major-mobile-efficiency-milestone
  14. ^ https://www.thurrott.com/hardware/236987/amd-delivers-a-major-mobile-efficiency-milestone
  15. ^ Гуалтьери, Дев (8 июля 2011 г.). «Предел Ландауэра». Блог Тикалон. Получено 2 июля, 2015.

дальнейшее чтение