Игу яньдуань - Yigu yanduan

Игу яньдуань (益 古 演 段 Старая математика в расширенных разделах) - математическая работа XIII века, написанная Династия Юань математик Ли Чжи.
Обзор
Игу яньдуань был основан на Северная песня математик Цзян Чжоу 's (蒋 周) Игу Джи (益 古 集 Сборник древней математики), который вымер. Однако из фрагментов, цитируемых в Ян Хуэй работа Полный алгоритм посевных площадей (田亩 比 类 算法 大全), этот утерянный математический трактат Игу Джи был о решении задач области с геометрией.
Ли Чжи использовал примеры Игу Джи представить искусство Тянь Юань Шу новичкам в этой сфере. Хотя предыдущая монография Ли Чжи Сеюань Хайцзин также использовал Тянь юань шу, это труднее понять, чем Игу яньдуань.
Игу яньдуань позже был собран в Сику Цюаньшу.
Игу яньдуань состоит из трех томов, в которых 64 задачи решены с использованием Тянь Юань ш] параллельно с геометрическим методом. Ли Чжи намеревался познакомить студентов с искусством Тянь юань шу через древнюю геометрию. Игу яньдуань вместе с Сеюань Хайцзин считаются основным вкладом в Тянь Юань Шу пользователя Li Zhi. Эти две работы также считаются самыми ранними дошедшими до нас документами о Тянь юань шу.
Все 64 задачи выполнялись более или менее в одном и том же формате, начиная с вопроса (问), за которым следует ответ (答曰), диаграмма, затем алгоритм (), в котором Ли Чжи шаг за шагом объяснил, как установить уравнение алгебры с Тянь Юань Шу, затем следует геометрическая интерпретация (Тяо дуань шу). Порядок расположения уравнения Тянь юань шу в Игу яньдуань является обратным тому, что в Ceyuan haijing, то есть здесь с постоянным членом вверху, за которым следуют тянь юань первого порядка, тянь юань второго порядка, тян юань третьего порядка и т. д. , Цинь Цзюшао Математический трактат в девяти разделах ), а позже стало нормой.
Игу яньдуань был впервые представлен английским читателям британским протестантским христианским миссионером в Китае, Александр Вайли кто написал:
Yi koo yen t'wan ... написанный в 1282 году, состоит из 64 геометрических задач, иллюстрирующих принцип измерения плоскости, эволюции и другие правила, все это разработано с помощью T'een yuen.[1]
В 1913 году Ван Хи перевел все 64 задачи на Игу яньдуань на французский.[2]
Том I

Задачи с 1 по 22, все о математике круга, заключенного в квадрат.
Пример: задача 8
Есть квадратное поле с круглым бассейном посередине, учитывая, что площадь земли составляет 13,75 му, а сумма окружностей квадратного поля и круглого бассейна равна 300 ступеням, каковы длины окружностей квадрата и круга. соответствующий?
Ответ: Окружность квадрата - 240 шагов, окружность круга - 60 шагов.
Метод: установите тянь юань один (небесный элемент 1) как диаметр круга, x
 TAI
TAI
умножьте его на 3, чтобы получить длину окружности в 3 раза (пи ~~ 3)
 TAI
TAI
вычтите это из суммы окружностей, чтобы получить длину окружности квадрата


 TAI
TAI
Его площадь в 16 раз больше площади квадрата.




 TAI
TAI



Снова установите тянь юань 1 как диаметр круга, возведите его в квадрат и умножьте на 12, чтобы получить площадь круга в 16 раз как
 TAI
TAI


вычтите из 16 временных квадратов площадь, у нас есть 16-кратная площадь земли




 TAI
TAI



поместите его справа и поставьте 16 раз 13,75 mu = 16 * 13,75 * 240 = 52800 шагов слева, после отмены получаем

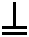


 TAI
TAI



Решите это уравнение, чтобы получить диаметр круга = 20 шагов, длина окружности = 60 шагов.
Том II

Задачи с 23 по 42, 20 задач во всей решающей геометрии прямоугольника, заключенного в круг с тянь юань шу
Пример, задача 35
Предположим, у нас есть круговое поле с прямоугольным бассейном с водой в центре, а расстояние от угла до окружности составляет 17,5 ступеней, а сумма длины и ширины бассейна составляет 85 ступеней, каков диаметр круга, длина и ширина бассейна?
Ответ: Диаметр круга равен 100 ступеням, длина бассейна - 60 ступеней, а ширина - 25 ступеней. Метод: Пусть диагональ прямоугольника равна единице тянь юань, тогда диаметр круга равен единице юаня плюс 17,5 * 2
умножьте квадрат диаметра на равняется четырехкратной площади круга:
вычитая четырехкратную площадь земли, получаем:
- в четыре раза больше бассейна = =
сейчас же
Квадрат суммы длины и ширины бассейна = 85 * 85 = 7225, что в четыре раза больше площади бассейна плюс квадрат разницы его длины и ширины ()
Кроме того, удвойте площадь бассейна плюс равно = квадрат диагонали бассейна, таким образом
(четырехкратная площадь бассейна + квадрат разницы в размерах) - (удвоенная площадь бассейна + квадрат, если разница в размерах) равно = вдвое больше бассейна
так в четыре раза больше площади бассейна =
приравняйте это с четырехкратной площадью бассейна, полученной выше
- =
мы получаем квадратное уравнение = 0 Решите это уравнение, чтобы получить
- диагональ бассейна = 65 ступеней
- диаметр круга = 65 + 2 * 17,5 = 100 шагов
- Длина - ширина = 35 шагов
- Длина + ширина = 85 шагов
- Длина = 60 шагов
- Ширина = 25 шагов
Том III

Задачи с 42 по 64, всего 22 вопроса по математике более сложных диаграмм.
В: пятьдесят четвертый. Поле квадратное, по диагонали - прямоугольный бассейн. Площадь за пределами бассейна - тысяча сто пятьдесят шагов. При том, что от углов поля до прямых сторон бассейна проходят четырнадцать шагов и девятнадцать шагов. Какая площадь квадратного поля, какова длина и ширина бассейна?
Ответ: Площадь квадратного поля - 40 квадратных шагов, длина бассейна - тридцать пять шагов, а ширина - двадцать пять шагов.
Пусть ширина бассейна будет Тяньюань 1.
 TAI
TAI
Добавьте ширину бассейна к удвоенному расстоянию от угла поля до короткой длинной стороны бассейна, равному длине диагонали поля x + 38


 TAI
TAI
Возведите его в квадрат, чтобы получить площадь квадрата с длиной диагонали бассейна в качестве сторон.




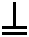
 TAI
TAI
- Длина бассейна минус ширина бассейна, умноженная на 2 = 2 (19-14) = 10
Длина бассейна = ширина бассейна +10: x + 10

 TAI
TAI
Площадь бассейна = бассейн с умножением на длину бассейна: x (x + 10) =
 TAI
TAI


Площадь бассейна раз 1,96 ( квадратный корень из 2 ) =1.4
надо


 Тай
Тай
Площадь диагонального квадрата за вычетом площади бассейна, умноженной на 1,96, равна площади земли, умноженной на 1,96:
- - :






 TAI
TAI
Занятые участки, умноженные на 1,96 = 1150 * 1,96 = 2254 =
следовательно =:





 TAI
TAI
Решив это уравнение, мы получим
ширина бассейна 25 шагов, поэтому длина бассейна = ширина бассейна +10 = 35 шагов длина бассейна = 45 шагов
Рекомендации
Чтение
- Ёсио Миками Развитие математики в Китае и Японии, стр81
- Аннотированный Игу яньдуань математиком династии Цин Ли Жуй.



















